Performance analysis of a continuous-time two-class global first-come-first-served queue with two servers and presorting | Annals of Operations Research Skip to main content
Springer Nature Link
Log in

Performance analysis of a continuous-time two-class global first-come-first-served queue with two servers and presorting

  • S.I.: QueueStochMod2019
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

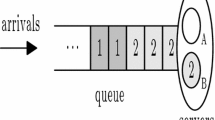
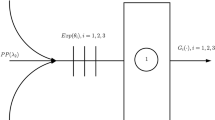
This paper considers a continuous-time queueing model with two types (classes) of customers each having their own dedicated server. The objective is to have a better grasp on the concept of a global first-come-first-served service discipline with presorting, i.e., all arriving customers are accommodated in one single FCFS queue, regardless of their type, with an exception of the first P customers. For the first P customers the FCFS rule holds only within the type, i.e., customers of different types can overtake each other in order to be served. Due to the global FCFS rule the model becomes non-workconserving and on the other hand we also have to keep track of the types of customers in the first P customers. The motivation of our work is the concept of a turn lane in road traffic, i.e., a lane reserved for vehicles making a specific turn at the next junction. This paper intends to be a step towards an analytic model to aid in the decision process of various policy makers of the optimal length of turn lanes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Baumann, H., & Sandmann, W. (2010). Numerical solution of level dependent quasi-birth-and-death processes. Procedia Computer Science, 1(1), 1561–1569.

    Article  Google Scholar 

  • Bruneel, H., Mélange, W., Steyaert, B., Claeys, D., & Walraevens, J. (2012). Influence of relative traffic distribution in nodes with blocking: an analytical model. In 26th European simulation and modelling conference, proceedings (pp. 136–143).

  • Bruneel, H., Mélange, W., Steyaert, B., Claeys, D., & Walraevens, J. (2013). Effect of global FCFS and relative load distribution in two-class queues with dedicated servers. 4OR, 11(4), 375–391.

    Article  Google Scholar 

  • Gail, H. R., Hantler, S. L., & Taylor, B. A. (2000). Use of characteristic roots for solving infinite state Markov chains. In Computational probability (pp. 205–255). Berlin: Springer.

  • Grassmann, W. (2003). The use of eigenvalues for finding equilibrium probabilities of certain Markovian two-dimensional queueing problems. INFORMS Journal on Computing, 15(4), 412–421.

    Article  Google Scholar 

  • Heidemann, D. (1996). A queueing theory approach to speed-flow-density relationships. In Proceedings of the 13th international symposium on transportation and traffic theory (pp. 103–118).

  • Kleinrock, L. (1975). Queueing systems, volume 1: theory. Hoboken: Wiley-Interscience.

    Google Scholar 

  • Mélange, W., Bruneel, H., Steyaert, B., & Walraevens, J. (2011). A two-class continuous-time queueing model with dedicated servers and global FCFS service discipline. Analytical and Stochastic Modeling Techniques and Applications, Lecture Notes in Computer Science, 6751, 14–27.

    Article  Google Scholar 

  • Neuts, M. (1981). Matrix-geometric solutions in stochastic models: An algorithmic approach. Baltimore: The John Hopkins University Press.

    Google Scholar 

  • Phung-Duc, T., Masuyama, H., Kasahara, S., & Takahashi, Y. (2010). A simple algorithm for the rate matrices of level-dependent QBD processes. In: Proceedings of the 5th international conference on queueing theory and network applications (pp. 46–52).

  • Sturm, J. (1985). Mémoire sur la résolution des équations numériques, mém savans etrang edn.

  • Van Woensel, T., & Vandaele, N. (2006). Empirical validation of a queueing approach to uninterrupted traffic flows. 4OR, 4, 59–72.

    Article  Google Scholar 

  • Van Woensel, T., & Vandaele, N. (2007). Modeling traffic flows with queueing models: A review. Asia-Pacific Journal of Operational Research, 24, 435–461.

    Article  Google Scholar 

  • Vandaele, N., Van Woensel, T., & Verbruggen, A. (2000). A queueing based traffic flow model. Transportation Research D, 5(2), 121–135.

    Article  Google Scholar 

  • Wilkinson, J. H. (1965). The algebraic eigenvalue problem. New York: Oxford University Press.

Download references

Acknowledgements

The authors wish to thank two reviewers for insightful comments that have strengthened the paper.

Author information

Authors and Affiliations

  1. Department of Telecommunications and Information Processing, Ghent University, Ghent, Belgium

    Willem Mélange, Joris Walraevens & Herwig Bruneel

Authors
  1. Willem Mélange
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joris Walraevens
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Herwig Bruneel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Joris Walraevens.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mélange, W., Walraevens, J. & Bruneel, H. Performance analysis of a continuous-time two-class global first-come-first-served queue with two servers and presorting. Ann Oper Res 310, 577–594 (2022). https://doi.org/10.1007/s10479-020-03741-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-020-03741-2

Keywords

Search

Navigation