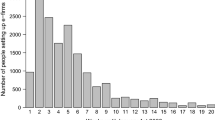
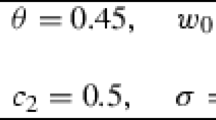Abstract
Income tax systems with “pass-through” entities transfer a firm’s income to shareholders, which are taxed individually. In 2014, a Chilean tax reform introduced this type of entity and changed to an accrual basis that distributes incomes (but not losses) to shareholders. A crucial step for the Chilean taxation authority is to compute the final income of each individual given the complex network of corporations and companies, usually including cycles between them. In this paper, we show the mathematical conceptualization and the solution to the problem, proving that there is only one way to distribute income to taxpayers. Using the theory of absorbing Markov chains, we define a mathematical model for computing the taxable income of each taxpayer, and we propose a decomposition algorithm for this problem. This approach allows us to compute the solution accurately and to efficiently use computational resources. Finally, we present some characteristics of Chilean taxpayers’ network and the computational results of the algorithm using this network.


Similar content being viewed by others
References
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., et al. (1999). LAPACK Users’ guide (Vol. 9). Philadelphia, PA: Society for Industrial and Applied Mathematics.
Bang-Jensen, J., & Gutin, G. Z. (2008). Digraphs: Theory, algorithms and applications. Berlin: Springer.
Berg, M., Waegenaere, A., & Wielhouwer, J. (2001). Optimal tax depreciation with uncertain future cash-flows. European Journal of Operational Research, 132(1), 197–209. https://doi.org/10.1016/S0377-2217(00)00132-6.
Björner, A., & Lovász, L. (1992). Chip-firing games on directed graphs. Journal of Algebraic Combinatorics, 1(4), 305–328.
Burnham, P. F. (2012). Taxing businesses through the individual income tax. Tech. rep., Congressional Budget Office, Congress of the United States. http://www.cbo.gov/publication/43750.
Cerqueti, R., & Coppier, R. (2014). A game theoretical analysis of the impact of income inequality and ethnic diversity on fiscal corruption. Annals of Operations Research, 243, 71–87. https://doi.org/10.1007/s10479-014-1567-9.
Coppersmith, D., & Winograd, S. (1987). Matrix multiplication via arithmetic progressions. In Proceedings of the nineteenth annual ACM symposium on theory of computing (pp. 1–6). ACM.
Engel, A. (1975). The probabilistic abacus. Educational Studies in Mathematics, 6(1), 1–22.
Goumagias, N., & Hristu-Varsakelis, D. (2013). Tax evasion by risk-averse firms in greece: A discrete markov-based optimization model. Optimization, 62(8), 1153–1167. https://doi.org/10.1080/02331934.2012.707654.
Goumagias, N., Hristu-Varsakelis, D., & Saraidaris, A. (2012). A decision support model for tax revenue collection in greece. Decision Support Systems, 53(1), 76–96.
Hartman, J., Liedtka, S., & Snyder, L. (2007). The impact of us tax depreciation law on asset location and ownership decisions. Computers and Operations Research, 34(12), 3560–3568. https://doi.org/10.1016/j.cor.2006.01.020.
Kulp, Ab, & Hartman, Jb. (2011). Optimal tax depreciation with loss carry-forward and backward options. European Journal of Operational Research, 208(2), 161–169. https://doi.org/10.1016/j.ejor.2010.06.040.
Le Gall, F. (2014). Powers of tensors and fast matrix multiplication. In Proceedings of the 39th international symposium on symbolic and algebraic computation (pp. 296–303). ACM.
Lee, Z. H., Deng, S., Lin, B., & Yang, J. (2010). Decision model and analysis for investment interest expense deduction and allocation. European Journal of Operational Research, 200(1), 268–280. https://doi.org/10.1016/j.ejor.2008.12.012.
Louveaux, F. (1982). Optimal scheduling of income tax prepayments under stochastic incomes. European Journal of Operational Research, 9(1), 26–32. https://doi.org/10.1016/0377-2217(82)90006-6.
Merino, C. (2005). The chip-firing game. Discrete Mathematics, 302(1), 188–210.
Miller, G., Weatherwax, M., Gardinier, T., Abe, N., Melville, P., Pendus, C., et al. (2012). Tax collections optimization for new york state. Interfaces, 42(1), 74–84. https://doi.org/10.1287/inte.1110.0618.
Tarjan, R. (1972). Depth-first search and linear graph algorithms. SIAM Journal on Computing, 1(2), 146–160.
Wang, Z., Gao, W., & Mukhopadhyay, S. (2016). Impact of taxation on international transfer pricing and offshoring decisions. Annals of Operations Research, 240(2), 683–707. https://doi.org/10.1007/s10479-013-1489-y.
World Bank (2015). Chile: Efectos distributivos de la reforma tributaria de 2014. Tech. rep., Ministerio de Hacienda, Gobierno de Chile. http://www.hacienda.cl/documento/descargar/id/15289.
Acknowledgements
The authors gratefully acknowledge the Department of Studies, Servicios Impuestos Internos, particularly Carlos Recabarren, for introducing us to the problem and its relevance and for their valuable collaboration that led us to obtain these results.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Barrera, J., Moreno, E. & Varas K., S. A decomposition algorithm for computing income taxes with pass-through entities and its application to the Chilean case. Ann Oper Res 286, 545–557 (2020). https://doi.org/10.1007/s10479-017-2707-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-017-2707-9