Abstract
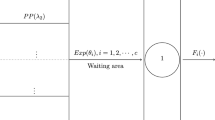
In operations research and networking problems, random-order-of-service (ROS) provides a well-known alternative to the classic first-come-first-served (FCFS) policy. Models with ROS policy are typically harder to analyze than their FCFS counterparts, with some performance measures notoriously hard to obtain. While significant progress has been realized in the analysis of random-order-of-service models with homogeneous customer service demands, the impact of heterogeneous customer demand is largely unknown. The current contribution studies this impact, with a discrete-time random-order-of-service queue serving customers with heterogeneous demands. Customer service times are independent random variables with type-dependent distribution. The numbers of new arrivals in each slot are independent and identically distributed over time, but can be type-correlated within a single slot. This corresponds to bursty input traffic generated by a finite number of sources, with one source for each type. The burstiness consists in correlation among sources (or types): the rate at which a source generates customers depends on the instantaneous rate of all other sources (and vice versa). Using a transform-based approach yields closed-form formulas for the first few moments of the customer waiting time. Facilitator is a multi-stage description of the customer sojourn, which allows establishing a relation between the so-called conditional waiting time and the actual steady-state customer waiting time. A somewhat unexpected result shows that, under certain conditions on the arrival and service processes, the random-order-of-service policy outperforms the first-come-first-served policy in terms of mean waiting time. A number of numerical examples illustrate this finding.







Similar content being viewed by others
References
Asmussen, S. (2003). Applied probability and queues (stochastic modelling and applied probability). New York: Springer.
Balmer, D. W. (1972). A single server queue in discrete time with customers served in random order. Journal of Applied Probability, 9(4), 862–867.
Barrer, D. Y. (1957). Queuing with impatient customers and indifferent clerks. Operations Research, 5(5), 644–649.
Borst, S. C., Boxma, O. J., Morrison, J. A., & Núñez Queija, R. N. (2003). The equivalence between processor sharing and service in random order. Operations Research Letters, 31, 254–262.
Boxma, O. J., & Takine, T. (2003). The M/G/1 FIFO queue with several customer classes. Queueing Systems, 45, 185–189.
Boxma, O. J., Foss, S. G., Lasgouttes, J. M., & Núñez Queija, R. N. (2004). Waiting time asymptotics in the single server queue with service in random order. Queueing Systems, 46(1/2), 35–73.
Bruneel, H., & Kim, B. G. (1993). Discrete-time models for communication systems including ATM. Boston: Kluwer.
Burke, P. J. (1959). Equilibrium delay distribution for one channel with constant holding time, poisson input and random service. Bell System Technical Journal, 38, 1021–1031.
Caulkins, J. P. (2010). Might randomization in queue discipline be useful when waiting cost is a concave function of waiting time? Socio-Economic Planning Sciences, 44, 19–24.
Cohen, J. W. (1982). The single server queue, 2nd edition. North-Holland.
Flatto, L. (1997). The waiting time distribution for the random order service M/M/1 queue. Annals of Applied Probability, 7(2), 382–409.
Haviv, M., & van der Wal, J. (1997). Equilibrium stategies for processor sharing and random queues with relative priorities. Probability in the Engineering and Informational Sciences, 11, 403–412.
Kelly, F. P. (1991). Effective bandwidths at multi-class queues. Queueing Systems, 9, 5–15. doi:10.1007/BF01158789.
Kim, J., Kim, J., & Kim, B. (2011). Analysis of the M/G/1 queue with discriminatory random order of service policy. Performance Evaluation, 68, 256–270.
Kingman, J. F. C. (1962). On queues in which customers are served in random order. Mathematical Proceedings of the Cambridge Philosophical Society, 58(01), 79–91.
Laevens, K., & Bruneel, H. (1995). Delay analysis for ATM queues with random order of service. Electronics Letters, 31(5), 346–347.
Laevens, K., & Bruneel, H. (1996). Useful relations in the analysis of ATM-queues fed by multiple types of traffic. Electronics Letters, 32(7), 631–632.
Larson, R. C., & Sasanuma, K. (2010). Congestion pricing: A parking queue model. Journal of Industrial and Systems Engineering, 4(1), 1–17.
Le Gall, P. (1962). Les Systèmes avec ou sans Attente et les Processus Stochastiques. Paris: Dunod.
Little, J. D. C. (1961). A proof for the queuing formula: L \(= \lambda \) W. Operations Research, 9(3), 383–387.
Palm, C. ( 1957). Waiting times with random served queue. Tele 1, pp. 1–107. (English ed., original from 1938)
Phipps, T. E., Jr, & Van Voorhis, W. R. (1956). Machine repair as a priority waiting-line problem. Operations Research, 4(1), 76–86.
Riordan, J. (1953). Delay curves for calls served at random. Bell System Technical Journal, 32, 100–119.
Sakai, Y., Takahashi, Y., & Hasegawa, T. (1998). Discrete time multi-class feedback queue with vacations and close-time under random order of service discipline. Journal of the Operations Research Society of Japan, 41(4), 589–613.
Takács, L. (1963). Delay distributions for one line with poisson input, general holding times, and various orders of service. Bell System Technical Journal, 42, 487–503.
Takagi, H. (1993). Queueing analysis volume 3: Discrete-time systems. North Holland: Elsevier Science Publishers.
Takine, T. (2001). Queue length distribution in a FIFO single-server queue with multiple arrival streams having different service time distributions. Queueing Systems, 39, 349–375.
Vaulot, E. (1946). Delais d’attente des appels téléphoniques traités au hasard. C.R. Acad. Sci. Paris, 222, 268–269.
Zwart, B. (2005). Heavy-traffic asymptotics for the single-server queue with random order of service. Operations Research Letters, 33(5), 511–518.
Acknowledgments
The authors wish to thank the anonymous reviewers for their valuable feedback, which greatly helped to improve this contribution. Part of this research has been funded by the Interuniversity Attraction Poles Programme initiated by the Belgian Science Policy Office. The first author is Postdoctoral Fellow with the Research Foundation Flanders (FWO-Vlaanderen).
Author information
Authors and Affiliations
Corresponding author
Appendix: Calculating the moments
Appendix: Calculating the moments
1.1 Notation
Taking partial derivatives at \((z,\bar{x})=(1,\bar{1})\) of e.g. \(F(z,\bar{x})=\text{ E }[z^{W^C} \bar{x}^{\bar{Q}^{C}}]\) gives the so-called factorial moments \(\text{ E }[W^C]\), \(\text{ E }[Q^C_i]\), \(\text{ E }[W^C(W^C-1)]\) and so on. Expressions for the corresponding (central) moments such as \(\text{ E }[(W^C)^2]\) and \(\text{ Var }[W^C]\), or covariances, then only require little additional algebra.
In the following, we will use a compact notation such as
and similar for higher-order derivatives.
Likewise, higher-order derivatives of \(A(\bar{x})\) at \(\bar{x}=\bar{1}\) are denoted by \(\lambda _{kl}\) (see also 3.2.4), where
and by \(\lambda _{klm}\) for third-order derivatives. Concerning moments of the service time, we will use the notation \(S'_k = S'_k(1)=\text{ E }[S_k]\), \(S''_k = S''_k(1)=\text{ E }[S_k(S_k-1)]\) and \(S'''_k=S'''_k(1)=\text{ E }[S_k(S_k-1)(S_k-2)]\).
Finally, it is beneficial to introduce following additional symbols:
1.2 Conditional waiting time
Taking the partial derivative with respect to \(z\) of Eq. (7), setting \((z,\bar{x})=(1,\bar{1})\) and rearranging terms somewhat gives
while the partial derivative with respect to \(x_i\) gives
Here \(I_z\) and \(I_i\) denoted partial derivatives at \((z,\bar{x})=(1,\bar{1})\) of \(I(z,\bar{x})\). Multiplying both sides of the latter with \(S'_i\), taking the sum for \(i=1 \ldots K\), renaming summation indices and rearranging terms once more, one finds
Here, recall that by definition \(\rho =\sum _{k=1}^K \lambda _k S'_k\). Inserting this in the equations above then immediately gives (8) and (9):
For the variance of the conditional waiting time, we need second-order derivatives. The procedure is much as the one outlined above, except that second-order derivatives of (7) now come into play. Taking the derivative with respect to \(z\) twice yields
Deriving once with respect to \(z\) and once with respect to \(x_i\) yields
Multiplying with \(S_i'\), taking the sum over \(i=1 \ldots K\), renaming indices and rearranging terms, now gives
Finally, taking double derivatives with respect to \(x_i\) and \(x_j\) yields
from which follows, similarly as above,
(where \(\mathcal {C}\) is given in (19)). Substituting back these intermediate results one by one ultimately gives
In this, only derivatives of known quantities (i.e., pgfs) appear. The variance can then be calculated via
1.3 Waiting time in equilibrium
Determining the moments of the waiting time in equilibrium requires the appropriate expressions for the partial derivatives of the pgf \(I_{m}(z,\bar{x})\) as given in (15).
Using (11) and (12), first-order partial derivatives yield
(which immediately gives (16)) and
In this, the first-order partial derivatives of the functions \(P_k(\bar{x})\) still appear. Putting \(\bar{x}=\bar{1}\) in (14) gives \(0=0\), while taking first-order partial derivatives with respect to \(x_i\) at \(\bar{x}=\bar{1}\) yields
(with \(P_k\) shorthand for \(P_k(\bar{1})\)). Multiplying with \(S'_i\), taking the sum for \(i=1,\ldots ,K\), renaming summation indices and rearranging somewhat then gives
Substituting back gives
Finally, the normalization condition \(Q(\bar{1})=\sum _k P_k = 1\) then learns that
from which \(\tilde{Q}(\bar{0})\) follows, and—by using this in Eq. (14)—also Eq. (13). It further establishes that \(P_k=\lambda _k/\lambda \), leading to the normalization constants for the pgfs \(Q_k(\bar{x})\) given in (12).
Taking second-order derivatives (with respect to \(x_i\) and then \(x_j\) at \(\bar{x}=\bar{1}\)) of (13) gives
with \(\delta _{ij}\) the Kronecker symbol. A key observation is that
so that we can introduce for these quantities the symbols \(P_{ki}=P_{ik}\). This follows directly from the definition of the (partial) pgfs \(P_k(\bar{x})\) as given in Section 3.2.2:
Using this in (26) and following the by now familiar procedure of multiplying with \(S'_i\), taking the sum over \(i=1,\ldots ,K\), using the fact that \(P_k=\lambda _k/\lambda \), renaming summation indices, rearranging terms, and repeating on the result the same procedure with respect to the index \(j\), gives
Substituting back then results in
Substituting further back yields an expression for \(P_{ki}\) but only the sum \(\sum _k P_{ki} S'_k\) given above is needed for calculating \(I_{i|m}\), see Eq. (24). Applying the result
of that calculation in (9) then ultimately yields Eq. (17).
For the variance of the waiting time in equilibrium, we need the second-order derivatives of \(I_m(z,\bar{x})\) at \((1,\bar{1})\), given Eq. (21) where they need to be substituted into. The most complex term involved therein is \(\sum _{k,l} I_{kl|m} S'_k S'_l\), which requires second-order derivatives of the functions \(P_k(\bar{x})\), in light of (15). Determining the latter requires taking up to third-order derivatives of Eq. (13) with respect to \(x_i\), \(x_j\) and \(x_l\) at \(\bar{x}=\bar{1}\), multiplying then with \(S'_i\), \(S'_j\) and \(S'_l\) respectively, each time summing over the corresponding index, substituting back and simplifying, as before. The algebra is straightforward, but rather tedious. In the end, one finds
Rights and permissions
About this article
Cite this article
Rogiest, W., Laevens, K., Walraevens, J. et al. Random-order-of-service for heterogeneous customers: waiting time analysis. Ann Oper Res 226, 527–550 (2015). https://doi.org/10.1007/s10479-014-1721-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-014-1721-4