Abstract
This paper analyzes the problem of selecting a set of items whose prices are to be updated in the next iteration in so called simple ascending auctions with unit-demand bidders. A family of sets called “sets in excess demand” is introduced, and the main result demonstrates that a simple ascending auction always terminates at the minimum Walrasian equilibrium prices if and only if the selection belongs to this family.

Similar content being viewed by others
Notes
The definition of “purely overdemanded sets” in Mo et al. (1988) is equivalent to our notion of excess demand. However, the paper by Mo et al. (1988) neither has been published nor is it available on the Internet (September, 2012). We are extremely grateful to Al Roth for providing us with a copy of the paper of Mo et al. (1988) in April, 2011, after we had completed the first version of this paper.
Proofs of Theorems 1–3 are available from the authors upon request.
A formal description of the Ford and Fulkerson (1956) method is available from the authors upon request.
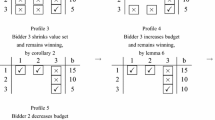
In the graph a set S t is fixed until some bidder b with D b (p t)⊆S t becomes indifferent to some item i∉D b (p t). In Fig. 1, this can be seen e.g. for the set S 0={3} and the price vector p 0=(0,0,0) where D 1(p 0)={3} but \(D_{1}(\hat{p})=\{1,3\}\) for \(\hat{p}=(0,0,8)\). Such an approach has previously been considered in related problems by e.g. Abdulkadiroğlu et al. (2004) and Andersson and Andersson (2012).
References
Abdulkadiroğlu, A., Sönmez, T., & Utku Ünver, M. (2004). Room assignment-rent division: a market approach. Social Choice and Welfare, 22, 515–538.
Abrache, J., Crainic, T. G., Gendreau, M., & Rekik, M. (2007). Combinatorial auctions. Annals of Operations Research, 153, 131–164.
Alkan, A., Demange, G., & Gale, D. (1991). Fair allocation of indivisible goods and criteria of justice. Econometrica, 59, 1023–1039.
Andersson, T., & Andersson, C. (2012). Properties of the DGS-auction algorithm. Computational Economics, 39, 113–133.
Andersson, T., & Svensson, L.-G. (2008). Non-manipulable assignment of individuals to positions revisited. Mathematical Social Sciences, 56, 350–354.
Ausubel, L. (2004). An efficient ascending-bid auction for multiple objects. The American Economic Review, 94, 1452–1475.
Ausubel, L. (2006). An efficient dynamic auction for heterogeneous commodities. The American Economic Review, 96, 602–629.
Bertsekas, D. P. (1988). The auction algorithm: a distributed relaxation method for the assignment problem. Annals of Operations Research, 14, 105–123.
Demange, G., & Gale, D. (1985). The strategy structure of two-sided matching markets. Econometrica, 53, 873–888.
Demange, G., Gale, D., & Sotomayor, M. (1986). Multi-item auctions. Journal of Political Economy, 94, 863–872.
Ford, L. R., & Fulkerson, D. R. (1956). Maximal flow through a network. Canadian Journal of Mathematics, 8, 299–404.
Gale, D. (1960). The theory of linear economic models. New York: McGraw-Hill.
Gul, F., & Stacchetti, E. (2000). The English auction with differentiated commodities. Journal of Economic Theory, 92, 66–95.
Hall, P. (1935). On representatives of subsets. Journal of the London Mathematical Society, 10, 26–30.
Leonard, H. B. (1983). Elicitation of honest preferences for the assignment of individuals to positions. Journal of Political Economy, 91(3), 461–479.
Mishra, D., & Talman, A. J. J. (2010). Characterization of the Walrasian equilibria of the assignment model. Journal of Mathematical Economics, 46, 6–20.
Mo, J.-P., Tsai, P.-S., & Lin, S.-C. (1988). Pure and minimal overdemanded sets: a note on Demange, Gale and Sotomayor. Unpublished Mimeo.
Perry, M., & Reny, P. (2005). An efficient multi-unit ascending auction. Review of Economic Studies, 72, 567–592.
Sankaran, J. K. (1994). On a dynamic auction mechanism for a bilateral assignment problem. Mathematical Social Sciences, 28, 143–150.
Shapley, L. S., & Shubik, M. (1972). The assignment game I: the core. International Journal of Game Theory, 1, 111–130.
Sun, N., & Yang, Z. (2009). Strategy-proof and privacy preserving fair allocation mechanism. Japanese Economic Review, 60, 143–151.
Svensson, L.-G. (1983). Large indivisibles: an analysis with respect to price equilibrium and fairness. Econometrica, 51, 939–954.
Thore, S. A., & Thompson, G. L. (1996). Exchanging heterogeneous goods via sealed bid auctions and transportation systems. Annals of Operations Research, 68, 181–208.
van der Laan, G., & Yang, Z. (2008). An ascending multi-item auction with financially constrained bidders (Tinbergen Institute Discussion Paper T1 2008–017/1).
Acknowledgements
The authors would like to thank Al Roth for guidance and assistance, and an anonymous referee for helpful suggestions. C. Andersson and T. Andersson would like to thank The Jan Wallander and Tom Hedelius Foundation for financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Andersson, T., Andersson, C. & Talman, A.J.J. Sets in excess demand in simple ascending auctions with unit-demand bidders. Ann Oper Res 211, 27–36 (2013). https://doi.org/10.1007/s10479-013-1344-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-013-1344-1