Strategies for protecting supply chain networks against facility and transportation disruptions: an improved Benders decomposition approach | Annals of Operations Research Skip to main content
Springer Nature Link
Log in

Strategies for protecting supply chain networks against facility and transportation disruptions: an improved Benders decomposition approach

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

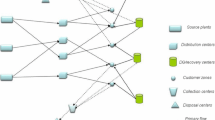
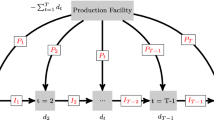
Disruptions rarely occur in supply chains, but their negative financial and technical impacts make the recovery process very slow. In this paper, we propose a capacitated supply chain network design (SCND) model under random disruptions both in facility and transportation, which seeks to determine the optimal location and types of distribution centers (DC) and also the best plan to assign customers to each opened DC. Unlike other studies in the extent literature, we use new concepts of reliability to model the strategic behavior of DCs and customers at the network: (1) Failure of DCs might be partial, i.e. a disrupted DC might still be able to serve with a portion of its initial capacity (2) The lost capacity of a disrupted DC shall be provided from a non-disrupted one and (3) The lost capacity fraction of a disrupted DC depends on its initial investment amount in the design phase.

In order to solve the proposed model optimally, a modified version of Benders’ Decomposition (BD) is applied. This modification tackles the difficulties of the BD’s master problem (MP), which ultimately improves the solution time of BD significantly. The classical BD approach results in low density cuts in some cases, Covering Cut Bundle (CCB) generation addresses this issue by generating a bundle of cuts instead of a single cut, which could cover more decision variables of the MP. Our inspiration to improve the CCB generation led to a new method, namely Maximum Density Cut (MDC) generation. MDC is based on the observation that in some cases CCB generation is cumbersome to solve in order to cover all decision variables of the MP rather than to cover part of them. Thus the MDC method generates a cut to cover the remaining decision variables which are not covered by CCB. Numerical experiments demonstrate the practicability of the proposed model to be promising in the SCND area, also the modified BD approach decreases the number of BD iterations and improves the CPU times, significantly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. Except Peng et al. (2011).

  2. Lim et al. (2010) defined that disruptions occur at unreliable DCs, and reliable DCs are the outsourcing ones which are secured against disruption and assumed to be uncapacitated.

  3. For example, consider a company which intends to supply its customers located in three different area zones. This must be planned in three particular modes: truck, rail and air in which the experience shows that many accidents (disruptions) have happened so far. Thus, this transportation strategy seems excessively risky. One proper safe strategy is to get assistance from outsources (similar to reliable DCs in Lim et al. 2010) in order to prevent the massive cost that company may be charged with; this is what we call safe transportation mode.

  4. If safe transportation mode in the primary assignment is used, there will be no need to use the secondary assignment, because the safe mode is also safe in disruption situation.

  5. The CCB method which is presented in this subsection is for the case of optimally cut, for feasibility cut refer to Saharidis et al. (2010).

  6. It should be noted that the literature of SCND under random disruption risks which utilize scenario-based approach (see Table 1, e.g. Peng et al. 2011 and Snyder and Daskin 2006), generate up to 65 scenarios for their instances.

  7. Hereafter we compile our investigation for medium and large sizes 80 and 120 by means of instances P24 and P28 in Table 2, respectively.

References

  • Altner, D. S., Ergun, O., & Uhan, N. A. (2010). The maximum flow network interdiction problem: valid inequalities, integrality gaps, and approximability. Operations Research Letters, 38(1), 33–38.

    Article  Google Scholar 

  • Andreas, A. K., & Smith, J. C. (2009). Decomposition algorithms for the design of a non simultaneous capacitated evacuation tree network. Networks, 53(2), 91–103.

    Article  Google Scholar 

  • Benders, J. F. (1962). Partitioning procedures for solving mixed-variables programming problems. Numerische Mathematik, 4(1), 238–252.

    Article  Google Scholar 

  • Berman, O., Krass, D., & Menezes, M. (2007). Facility reliability issues in network p-median problems: strategic centralization and co-location effects. Operations Research, 55(2), 332–350.

    Article  Google Scholar 

  • Berman, O., Krass, D., & Menezes, M. (2009). Locating facilities in the presence of disruptions and incomplete information. Decision Sciences, 40(4), 845–868.

    Article  Google Scholar 

  • Chopra, S., & Sodhi, M. S. (2004). Managing risk to avoid supply-chain breakdown. MIT Sloan Management Review, 46(1), 53–61.

    Google Scholar 

  • Chopra, S., Reinhardt, G., & Mohan, U. (2007). The importance of decoupling recurrent and disruption risks in a supply chain. Naval Research Logistics, 54(5), 544–555.

    Article  Google Scholar 

  • Church, R. L., & Scaparra, M. P. (2006). Protecting critical assets: the R-interdiction median problem with fortification. Geographical Analysis, 39(2), 129–146.

    Article  Google Scholar 

  • Church, R. L., Scaparra, M. P., & Middleton, R. S. (2004). Identifying critical infrastructure: the median and covering facility interdiction problem. Annals of the Association of American Geographers, 94(3), 491–502.

    Article  Google Scholar 

  • Colbourn, C. (1987). The combinatorics of network reliability. New York: Oxford University Press.

    Google Scholar 

  • Conejo, A. J., Castillo, E., Minguez, R., & Garcia-Bertrand, R. (2006). Decomposition techniques in mathematical programming. In Engineering and science applications. Berlin: Springer.

    Google Scholar 

  • Cordeau, J. F., Soumis, F., & Desrosiers, J. (2000). A Benders decomposition approach for the locomotive and car assignment problem. Transportation Science, 34(2), 133–149.

    Article  Google Scholar 

  • Cordeau, J. F., Pasin, F., & Solomon, M. M. (2006). An integrated model for logistics network design. Annals of Operations Research, 144(1), 59–82.

    Article  Google Scholar 

  • Cote, G., & Laughton, M. (1984). Large-scale mixed integer programming: Benders-type heuristics. European Journal of Operational Research, 16, 327–333.

    Article  Google Scholar 

  • Craighead, C. W., Blackhurst, J., Rungtusanatham, M. J., & Handfield, R. B. (2007). The severity of supply chain disruptions: Design characteristics and mitigation capabilities. Decision Sciences, 38(1), 131–156.

    Article  Google Scholar 

  • Cui, T., Ouyang, Y., & Shen, Z.-J. (2010). Reliable facility location design under the risk of disruptions. Operations Research, 58(4), 998–1011.

    Article  Google Scholar 

  • Drezner, Z. (1987). Heuristic solution methods for two location problems with unreliable facilities. Journal of Operations Research Society, 38(6), 509–514.

    Google Scholar 

  • Elkins, D., Handfield, R. B., Blackhurst, J., & Craighead, C. W. (2005). 18 ways to guard against disruption. Supply Chain Management Review, 9(1), 46–53.

    Google Scholar 

  • Kleindorfer, P. R., & Saad, G. (2005). Managing disruption risks in supply chains. Production and Operations Management, 14(1), 53–68.

    Article  Google Scholar 

  • Klibi, W., Martel, A., & Guitouni, A. (2010). The design of robust value-creating supply chain networks: a critical review. European Journal of Operational Research, 203(2), 283–293.

    Article  Google Scholar 

  • Kraiselburd, S., Narayanan, V. G., & Raman, A. (2004). Contracting in a supply chain with stochastic demand and substitute products. Production and Operations Management, 13(1), 46–62.

    Article  Google Scholar 

  • Kaut, M., Wallace, S. W., Vladimirou, H., & Zenios, S. (2007). Stability analysis of portfolio management with conditional value-at-risk. Quantitative Finance, 7(4), 397–409.

    Article  Google Scholar 

  • Kulkarni, S. S., Magazine, M. J., & Raturi, A. S. (2004). Risk pooling advantages of manufacturing network configuration. Production and Operations Management, 13(2), 186–199.

    Article  Google Scholar 

  • Lee, S. D. (2001). On solving unreliable planar location problems. Computers & Operations Research, 28(4), 329–344.

    Article  Google Scholar 

  • Li, X., & Ouyang, Y. (2010). A continuum approximation approach to reliable facility location design under correlated probabilistic disruptions. Transportation Research. Part B, 44(4), 535–548.

    Article  Google Scholar 

  • Liberatore, F., Scaparra, M. P., & Daskin, M. S. (2011). Analysis of facility protection strategies against an uncertain number of attacks: the stochastic R-interdiction median problem with fortification. Computers & Operations Research, 38(1), 357–366.

    Article  Google Scholar 

  • Liberatore, F., Scaparra, M. P., & Daskin, M. S. (2012). Hedging against disruptions with ripple effects in location analysis. Omega, 40, 21–30.

    Article  Google Scholar 

  • Lim, M., Daskin, M., Bassamboo, A., & Chopra, S. (2010). A facility reliability problem: formulation, properties and algorithm. Naval Research Logistics, 57(1), 58–70.

    Google Scholar 

  • Magnanti, T., & Wong, R. (1981). Accelerating Benders decomposition algorithmic enhancement and model selection criteria. Operations Research, 29, 464–484.

    Article  Google Scholar 

  • Martinez-de-Albeniz, V., & Simchi-Levi, D. (2005). A portfolio approach to procurement contracts. Production and Operations Management, 14(1), 90–114.

    Article  Google Scholar 

  • McDaniel, D., & Devine, M. (1977). A modified Benders partitioning algorithm for mixed integer programming. Management Science, 24, 312–319.

    Article  Google Scholar 

  • Mohebbi, E. (2004). A replenishment model for the supply-uncertainty problem. International Journal of Production Economics, 87, 25–37.

    Article  Google Scholar 

  • Oke, A., & Gopalakrishnan, M. (2009). Managing disruptions in supply chains: a case study of a retail supply chain. International Journal of Production Economics, 181, 168–174.

    Article  Google Scholar 

  • Papadakos, N. (2008). Practical enhancements to the Magnanti-Wong method. Operations Research Letters, 36(4), 444–449.

    Article  Google Scholar 

  • Parlar, M. (1997). Continuous review inventory problem with random supply interruptions. European Journal of Operational Research, 99, 366–385.

    Article  Google Scholar 

  • Parlar, M., & Berkin, D. (1991). Future supply uncertainty in EOQ models. Naval Research Logistics, 38, 107–121.

    Article  Google Scholar 

  • Peng, P., Snyder, L. V., Lim, A., & Liu, Z. (2011). Reliable logistics networks design with facility disruptions. Transportation Research. Part B. doi:10.1016/j.trb.2011.05.022.

    Google Scholar 

  • Qi, L., Shen, Z.-J., & Snyder, L. V. (2010). The effect of supply disruptions on supply chain design decisions. Transportation Science, 44(2), 274–289.

    Article  Google Scholar 

  • Rei, W., Gendreau, M., Cordeau, J. F., & Soriano, P. (2006). Accelerating Benders decomposition by local branching. In: Hybrid methods and branching rules in combinatorial optimization, Montreal, 2006.

    Google Scholar 

  • Saharidis, G. K. D., & Ierapetritou, M. G. (2010). Improving Benders decomposition using maximum feasible subsystem (MFS) cut generation strategy. Computers & Chemical Engineering, 8(34), 1237–1245.

    Article  Google Scholar 

  • Saharidis, G. K. D., Minoux, M., & Dallery, Y. (2009). Scheduling of loading and unloading of crude oil in a refinery using event-based discrete time formulation. Computers & Chemical Engineering, 33(8), 1413–1426.

    Article  Google Scholar 

  • Saharidis, G. K. D., Minoux, M., & Ierapetritou, M. G. (2010). Accelerating Benders method using covering cut bundle generation. International Transactions in Operational Research, 17(2), 221–237.

    Article  Google Scholar 

  • Saharidis, G. K. D., Boile, M., & Theofanis, S. (2011). Initialization of the Benders master problem using valid inequalities applied to fixed-charge network problems. Expert Systems with Applications. doi:10.1016/j.eswa.2010.11.075.

    Google Scholar 

  • Scaparra, M. P., & Church, R. L. (2008). A bi level mixed-integer program for critical infrastructure protection planning. Computers & Operations Research, 35(6), 1905–1923.

    Article  Google Scholar 

  • Sherali, H. F., & Lunday, B. J. (2011). On generating maximal non dominated Benders cuts. Annals of Operations Research. doi:10.1007/s10479-011-0883-6.

    Google Scholar 

  • Shier, D. R. (1991). Network reliability and algebraic structures. Oxford: Clarendon Press.

    Google Scholar 

  • Shooman, M. L. (2002). Reliability of computer systems and networks: fault tolerance, analysis, and design. New York: Wiley.

    Google Scholar 

  • Snyder, L. V., & Daskin, M. S. (2005). Reliability models for facility location: the expected failure cost case. Transportation Science, 39(3), 400–416.

    Article  Google Scholar 

  • Snyder, L. V., & Daskin, M. S. (2006). Stochastic p-robust location problems. IIE Transactions, 38(11), 971–985.

    Article  Google Scholar 

  • Snyder, L. V., Scaparra, M. P., Daskin, M. S., & Church, R. L. (2006). Planning for disruptions in supply chain networks. In: Tutorials in operations research INFORMS 2006 (pp. 234–257).

    Google Scholar 

  • Tang, C. S. (2006). Perspectives in supply chain risk management. International Journal of Production Economics, 103, 451–488.

    Article  Google Scholar 

  • Tomlin, B. (2006). On the value of mitigation and contingency strategies for managing supply chain disruption risks. Management Science, 52(5), 639–657.

    Article  Google Scholar 

  • Tomlin, B., & Wang, Y. (2005). On the value of mix flexibility and dual sourcing in unreliable newsvendor networks. Manufacturing & Service Operations Management, 7(1), 37–57.

    Article  Google Scholar 

  • Wagner, S. M., & Bode, C. (2006). An empirical investigation into supply chain vulnerability. Journal of Purchasing and Supply Management, 12(6), 301–312.

    Article  Google Scholar 

  • Zakeri, G., Philpott, A. B., & Ryan, D. M. (1998). Inexact cuts in benders decomposition. SIAM Journal on Optimization, 10(3), 643–657.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Amirkabir University of Technology, Tehran, Iran

    Nader Azad & Hamid Davoudpour

  2. Kathikas Institute of Research & Technology, Columbus, MO, USA

    Georgios K. D. Saharidis

  3. University of Thessaly, Leoforos Athinon, Pedion Areos, 38834, Volos, Greece

    Georgios K. D. Saharidis

  4. School of Industrial Engineering, Islamic Azad University–South Tehran Branch, Tehran, Iran

    Hooman Malekly

  5. Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran

    Seyed Alireza Yektamaram

Authors
  1. Nader Azad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Georgios K. D. Saharidis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hamid Davoudpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hooman Malekly
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Seyed Alireza Yektamaram
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Georgios K. D. Saharidis.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Azad, N., Saharidis, G.K.D., Davoudpour, H. et al. Strategies for protecting supply chain networks against facility and transportation disruptions: an improved Benders decomposition approach. Ann Oper Res 210, 125–163 (2013). https://doi.org/10.1007/s10479-012-1146-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-012-1146-x

Keywords

Search

Navigation