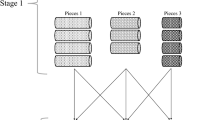
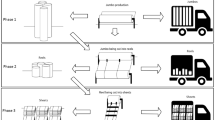
Abstract
We describe a new hierarchical 2D-guillotine Cutting Stock Problem. In contrast to the classic cutting stock problem, waste is not an issue. The problem relates to the removal of a defective part and assembly of the remaining parts into homogeneous size blocks. The context is the packing stages of cake manufacturing. The company’s primary objective is to minimise total processing time at the subsequent, packing stage. This objective reduces to one of minimising the number of parts produced when cutting the tray load of buns. We offer a closed form optimization approach to this class of problems for certain cases, without recourse to mathematical programming or heuristics. The methodology is demonstrated through a case study in which the number of parts is reduced by almost a fifth, and the manufacturer’s subsidiary requirement to reduce isolated single bun parts and hence customer complaints is also satisfied.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Aboudi, R., & Barcia, P. (1998). Determining cutting stock patterns when defects are present. Annals of Operation Research, 82, 343–354.
Christofides, N., & Hadjiconstantinou, E. (1995). An exact algorithm for orthogonal 2-D cutting problems using guillotine cuts. European Journal of Operational Research, 83, 21–38.
Christofides, N., & Whitlock, C. (1977). An algorithm for two-dimensional cutting problems. Operations Research, 25, 30–44.
Cui, Y. (2004). Generating optimal multiple-segment cutting patterns for rectangular blanks. Proceedings of the Institution of Mechanical Engineers. Part B. Journal of Engineering Manufacturing, 218(11), 1483–1490.
Dyckhoff, H. (1990). A typology of cutting and packing problems. European Journal of Operational Research, 44, 145–159.
Dyckhoff, H. G., Scheithauer, J., & Terno, M. (1997). Cutting and packing. In F. Dell’Amico, F. Maffioli, & S. Martello (Eds.), Annotated bibliographies in combinatorial optimization (pp. 393–412). New York: Wiley.
Gilmore, P., & Gomory, R. (1965). Multistage cutting stock problems of two and more dimensions. Operations Research, 13, 94–120.
Gilmore, P., & Gomory, R. (1966). The theory and computation of knapsack functions. Operations Research, 14, 1045–1074.
Hahn, S. (1968). On the optimal cutting of defective sheets. Operations Research, 16, 1100–1114.
Herz, J. C. (1972). Recursive computational procedure for two-dimensional stock cutting. IBM Journal of Research and Development, 16(5), 462–469.
Hifi, M. (1997). An improvement of Viswanathan and Bagchi’s exact algorithm for constrained two-dimensional cutting stock. Computers & Operations Research, 24(8), 727–736.
Hifi, M. (2001). Exact algorithms for large-scale unconstrained two and three staged cutting problems. Computer Optimization and Application, 16, 63–88.
Hifi, M., & M’Hallah, R. (2005). An exact algorithm for constrained two-dimensional two-staged cutting problems. Operations Research, 53(1), 140–150.
Hong, L., Guangzhou, Z., & Zongkai, L. (1997). A system of optimizing nesting with analogical learning mechanism. Computers & Industrial Engineering, 32(4), 713–725.
Lodi, A., & Monaci, M. (2003). Integer linear programming models for 2-staged two-dimensional Knapsack problems. Mathematical Programming Series B, 94, 257–278.
Ronnqvist, M. (1995). A method for the cutting stock problem with different qualities. European Journal of Operational Research, 83, 57–68.
Ronnqvist, M., & Astrand, E. (1998). Integrated defect detection and optimization for cross cutting of wooden boards. European Journal of Operational Research, 108, 490–508.
Sarker, B. R. (1988). An optimum solution for one-dimensional slitting problems—a dynamic-programming approach. Journal of the Operational Research Society, 39, 749–755.
Smith, N. R., Al Khayyal, F., & Griffin, P. (2000). A tree-search method for solving a cutting stock assignment problem. International Journal of Production Research, 38, 1557–1578.
Sweeney, P. E., & Haessler, R. W. (1990). One-dimensional cutting stock decisions for rolls with multiple quality grades. European Journal of Operational Research, 44, 224–231.
Sweeney, P. E., & Paternoster, R. E. (1992). Cutting and packing problems—a categorized, application-orientated research bibliography. Journal of the Operational Research Society, 43, 691–706.
van Oostrum, J. M. (2004) Bun splitting (Technical Report Thesis). University of Twente, Enschede, The Netherlands, p. 62.
Wascher, G. H., HauBner, H., & Schumann, H. (2007). An improved typology of cutting and packing problems. European Journal of Operational Research, 183, 1109–1130.
Yanasse, H. H., & Katsurayama, D. M. (2008). An enumeration scheme to generate constrained exact checkerboard patterns. Computers & Operations Research, 35, 2114–2128.
Yanasse, H. H., & Morabito, R. (2006). Linear models for 1-group 2-dimensional guillotine cutting problems. International Journal of Production Research, 44(17), 3471–3491.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Glass, C.A., van Oostrum, J.M. Bun splitting: a practical cutting stock problem. Ann Oper Res 179, 15–33 (2010). https://doi.org/10.1007/s10479-008-0458-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-008-0458-3