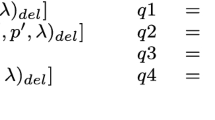Abstract
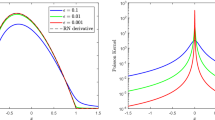
The numerical solution of dynamical systems with memory requires the efficient evaluation of Volterra integral operators in an evolutionary manner. After appropriate discretization, the basic problem can be represented as a matrix-vector product with a lower diagonal but densely populated matrix. For typical applications, like fractional diffusion or large-scale dynamical systems with delay, the memory cost for storing the matrix approximations and complete history of the data then becomes prohibitive for an accurate numerical approximation. For Volterra integral operators of convolution type, the fast and oblivious convolution quadrature method of Schädle, Lopez-Fernandez, and Lubich resolves this issue and allows to compute the discretized evaluation with N time steps in \(O(N \log N)\) complexity and only requires \(O(\log N)\) active memory to store a compressed version of the complete history of the data. We will show that this algorithm can be interpreted as an \({{\mathscr{H}}}\)-matrix approximation of the underlying integral operator. A further improvement can thus be achieved, in principle, by resorting to \({{\mathscr{H}}}^{2}\)-matrix compression techniques. Following this idea, we formulate a variant of the \({{\mathscr{H}}}^{2}\)-matrix-vector product for discretized Volterra integral operators that can be performed in an evolutionary and oblivious manner and requires only O(N) operations and \(O(\log N)\) active memory. In addition to the acceleration, more general asymptotically smooth kernels can be treated and the algorithm does not require a priori knowledge of the number of time steps. The efficiency of the proposed method is demonstrated by application to some typical test problems.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Alpert, B., Greengard, L., Hagstrom, T.: Rapid evaluation of nonreflecting boundary kernels for time-domain wave propagation. SIAM J. Numer. Anal. 37(4), 1138–1164 (2000)
Amari, S.: Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 27(2), 77–87 (1977)
Arendt, W., Batty, C.J.K., Hieber, M., Neubrander, F.: Vector-Valued Laplace Transforms and Cauchy Problems. Springer Basel, Basel (2011)
Baffet, D., Hesthaven, J.S.: A kernel compression scheme for fractional differential equations. SIAM J. Numer. Anal. 55(2), 496–520 (2017)
Börm, S.: Efficient Numerical Methods for Non-Local Operators, volume 14 of EMS Tracts in Mathematics, European Mathematical Society (EMS) Zürich (2010)
Brandt, A., Lubrecht, A.A.: Multilevel matrix multiplication and fast solution of integral equations. J. Comput. Phys. 90(2), 348–370 (1990)
Brunner, H.: Collocation Methods for Volterra Integral and Related Functional Differential Equations. Number 15 in Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (2004)
Brunner, H.: Volterra Integral Equations: An Introduction to Theory and Applications. Cambridge University Press, Cambridge (2017)
Cuesta, E., Lubich, C., Palencia, C.: Convolution quadrature time discretization of fractional diffusion-wave equations. Math. Comput. 75 (254), 673–697 (2006)
Dahmen, W., Prössdorf, S., Schneider, R.: Wavelet approximation methods for pseudodifferential equations II: matrix compression and fast solution. Adv. Comput. Math. 1(3), 259–335 (1993)
Dingfelder, B., Weideman, J.A.C.: An improved Talbot method for numerical Laplace transform inversion. Numer. Algorithm. 68(1), 167–183 (2015)
Dölz, J., Egger, H., Shashkov, V: A convolution quadrature method for Maxwell’s equations in dispersive media (2020)
Egger, H., Schmidt, K., Shashkov, V.: Multistep and Runge-Kutta convolution quadrature methods for coupled dynamical systems. J. Comput. Appl. Math. 387, 112618 (2020)
Fong, W., Darve, E.: The black-box fast multipole method. J. Comput. Phys. 228(23), 8712–8725 (2009)
Giebermann, K.: Multilevel approximation of boundary integral operators. Computing 67(3), 183–207 (2001)
Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987)
Hackbusch, W.: A sparse matrix arithmetic based on \({\mathscr{H}}\)-matrices part I: introduction to \({\mathscr{H}}\)-matrices. Computing 62(2), 89–108 (1999)
Hackbusch, W.: Hierarchical Matrices: Algorithms and Analysis. Springer, Heidelberg (2015)
Hackbusch, W., Nowak, Z.P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numer. Math. 54(4), 463–491 (1989)
Hagstrom, T.: Radiation boundary conditions for the numerical simulation of waves. Acta Numerica 8, 47–106 (1999)
Hairer, E., Lubich, C. h., Schlichte, M.: Fast numerical solution of nonlinear Volterra convolution equations. SIAM J. Sci. Stat. Comput. 6(3), 532–541 (1985)
Jiang, S., Greengard, L.: Fast evaluation of nonreflecting boundary conditions for the Schrödinger equation in one dimension. Comput. Math. Appl. 47(6-7), 955–966 (2004)
Jiang, S., Greengard, L.: Efficient representation of nonreflecting boundary conditions for the time-dependent Schrödinger equation in two dimensions. Commun. Pure Appl. Math. 61(2), 261–288 (2008)
Kapur, S., Long, D.E., Roychowdhury, J.: Efficient time-domain simulation of frequency-dependent elements. In: Proceedings of International Conference on Computer Aided Design, pp 569–573. IEEE Comput. Soc. Press, San Jose, CA, USA (1996)
Kaye, J., Golež, D.: Low rank compression in the numerical solution of the nonequilibrium Dyson equation. SciPost Phys. 10(4), 091 (2021)
López-Fernández, M., Palencia, C., Schädle, A.: A spectral order method for inverting sectorial laplace transforms. SIAM J. Numer. Anal. 44(3), 1332–1350 (2006)
Lubich, C.H.: Convolution quadrature and discretized operational calculus. I. Numer. Math. 52(2), 129–145 (1988)
Lubich, C.H.: Convolution quadrature discretized operational calculus. II. Numer. Math. 52(4), 413–425 (1988)
Lubich, C.H.: Convolution quadrature revisited. BIT Numer. Math. 44(3), 503–514 (2004)
Lubich, C.H., Ostermann, A.: Runge-Kutta methods for parabolic equations and convolution quadrature. Math. Comput. 60(201), 105–105 (1993)
Lubich, C.H., Schädle, A.: Fast convolution for nonreflecting boundary conditions. SIAM J. Sci. Comput. 24(1), 161–182 (2002)
Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1–77 (2000)
Rokhlin, V.: Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 60(2), 187–207 (1985)
Sayas, F.-J.: Retarded Potentials and Time Domain Boundary Integral Equations, volume 50 of Springer Series in Computational Mathematics. Springer International Publishing, Cham (2016)
Schädle, A., López-Fernández, M., Lubich, C.H.: Fast and oblivious convolution quadrature. SIAM J. Sci. Comput. 28(2), 421–438 (2006)
Sova, M.: The Laplace transform of analytic vector-valued functions (complex conditions). Čas. pro pěstování matematiky 104(3), 267–280 (1979)
Talbot, A.: The accurate numerical inversion of laplace transforms. IMA J. Appl. Math. 23(1), 97–120 (1979)
Acknowledgements
The authors would like to thank the first reviewer for an exceptionally careful reading and valuable comments and remarks.
Funding
Open Access funding enabled and organized by Projekt DEAL. Support by the German Science Foundation (DFG) via TRR 146 (project C3), TRR 154 (project C04), and SPP 2256 (project Eg-331/2-1) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Michael O’Neil
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Advances in Computational Integral Equations
Guest Editors: Stephanie Chaillat, Adrianna Gillman, Per-Gunnar Martinsson, Michael O’Neil, Mary-Catherine Kropinski, Timo Betcke, Alex Barnett
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dölz, J., Egger, H. & Shashkov, V. A fast and oblivious matrix compression algorithm for Volterra integral operators. Adv Comput Math 47, 81 (2021). https://doi.org/10.1007/s10444-021-09902-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10444-021-09902-6
Keywords
- Volterra integral operators
- Convolution quadrature
- \({{\mathscr{H}}}^{2}\)-matrices
- Matrix compression