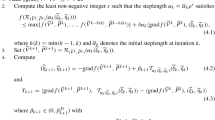Abstract
The l parameterized generalized eigenvalue problems for the nonsquare matrix pencils, proposed by Chu et al.in 2006, can be formulated as an optimization problem on a corresponding complex product Stiefel manifold. In this paper, an effective and efficient algorithm based on the Riemannian Newton’s method is established to solve the underlying problem. Under our proposed framework, to solve the corresponding Newton’s equation, it can be converted to solve a standard real symmetric linear system with a dimension reduction. By combining the Riemannian curvilinear search method with Barzilai–Borwein steps, a hybrid algorithm with both global and quadratic convergence is obtained. Numerical experiments are provided to illustrate the efficiency of the proposed method. Detailed comparisons with some latest methods are also provided to show the merits of the proposed approach.
Similar content being viewed by others
References
Absil, P.A., Baker, C., Gallivan, K.: A truncated-CG style method for symmetric generalized eigenvalue problems[J]. J. Comput. Appl. Math. 189(1-2), 274–285 (2006)
Boutry, G., Elad, M., Golub, G.H., Milanfar, P.: The generalized eigenvalue problem for nonsquare pencils using a minimal perturbation approach[J]. SIAM J. Matrix Anal. Appl. 27(2), 582–601 (2005)
Chu, D., Golub, G.H.: On a generalized eigenvalue problem for nonsquare pencils[J]. SIAM J. Matrix Anal. Appl. 28(3), 770–787 (2006)
Kressner, D., Mengi, E., Nakić, I., Truhar, N.: Generalized eigenvalue problems with specified eigenvalues[J]. IMA J. Numer. Anal. 34(2), 480–501 (2014)
Lecumberri, P., Gómez, M., Carlosena, A.: Generalized eigenvalues of nonsquare pencils with structure[J]. SIAM J. Matrix Anal. Appl. 30(1), 41–55 (2008)
Ito, S., Murota, K.: An algorithm for the generalized eigenvalue problem for nonsquare matrix pencils by minimal perturbation approach[J]. SIAM J. Matrix Anal. Appl. 37(1), 409–419 (2016)
Zheng, H., Liu, L.: The sign-based methods for solving a class of nonlinear complementarity problems[J]. J. Optim. Theory Appl. 180(2), 480–499 (2019)
Golub, G.H., Loan, C.F.V.: An analysis of the total least squares problem[J]. SIAM J. Numer. Anal. 17(6), 883–893 (1980)
Li, J.F., Li, W., Vong, S.W., Luo, Q.L., Xiao, M.: A Riemannian optimization approach for solving the generalized eigenvalue problem for nonsquare matrix pencils[J]. J. Sci. Comput. 82(3), 1–43 (2020)
Sato, H., Iwai, T.: A Riemannian optimization approach to the matrix singular value decomposition[J]. SIAM J. Optim. 23(1), 188–212 (2013)
Sato, H., Iwai, T.: A complex singular value decomposition algorithm based on the Riemannian Newton method[C]. In: 52nd IEEE Conference on Decision and Control, pp. 2972–2978. IEEE (2013)
Sato, H.: Riemannian conjugate gradient method for complex singular value decomposition problem[C]. In: 53rd IEEE Conference on Decision and Control, pp. 5849–5854. IEEE (2014)
Aihara, K., Sato, H.: A matrix-free implementation of Riemannian Newton’s method on the Stiefel manifold[J]. Optim. Lett. 11(8), 1729–1741 (2017)
Sato, H.: Riemannian Newton-type methods for joint diagonalization on the Stiefel manifold with application to independent component analysis[J]. Optimization 66(12), 2211–2231 (2017)
Li, J.F., Wen, Y.Q., Zhou, X.L., Wang, K.: Effective algorithms for solving trace minimization problem in multivariate statistics[J]. Mathematical Problems in Engineering, 2020, 2020:Article ID 3054764
Wen, Z., Yin, W.: A feasible method for optimization with orthogonality constraints[J]. Math. Program. 142(1-2), 397–434 (2013)
Hu, J., Liu, X., Wen, Z.W., Yuan, Y.X.: A brief introduction to manifold optimization[J]. J. Oper. Res. Soc. China 8(2), 199–248 (2020)
Henderson, H.V., Searle, S.R.: The vec-permutation matrix, the vec operator and Kronecker products: A review[J]. Linear Multilinear Algebra 9(4), 271–288 (1981)
Yuan, S., Liao, A., Lei, Y.: Least squares Hermitian solution of the matrix equation (AXB, CXD) = (E, F) with the least norm over the skew field of quaternions[J]. Math. Comput. Model. 48(1-2), 91–100 (2008)
Sun, J.: Matrix perturbation Analysis[M] science press (2001)
Absil, P.A., Mahony, R., Sepulchre, R.: Optimization algorithms on matrix Manifolds[M]. Princeton University Press (2009)
Edelman, A., Arias, T.A., Smith, S.T.: The geometry of algorithms with orthogonality constraints[J]. SIAM J. Matrix Anal. Appl. 20(2), 303–353 (1998)
Absil, P.A., Mahony, R., Trumpf, J.: An extrinsic look at the Riemannian Hessian[C]. In: International Conference on Geometric Science of Information, pp. 361–368. Springer (2013)
Zhu, X.: A Riemannian conjugate gradient method for optimization on the Stiefel manifold[J]. Comput. Optim. Appl. 67(1), 73–110 (2017)
Saad, Y.: Iterative Methods for Sparse Linear Systems[M], vol. 82. SIAM (2003)
Barzilai, J., Borwein, J.M.: Two-point step size gradient methods[J]. IMA J. Numer. Anal. 8(1), 141–148 (1988)
Boumal, N., Mishra, B., Absil, P.A., Sepulchre, R.: Manopt, a Matlab toolbox for optimization on manifolds[J]. J. Mach. Learn. Res. 15(1), 1455–1459 (2014)
Yao, T.T., Bai, Z.J., Zhao, Z., Ching, W.K.: A Riemannian Fletcher–Reeves conjugate gradient method for doubly stochastic inverse eigenvalue problems[J]. SIAM J. Matrix Anal. Appl. 37(1), 215–234 (2016)
Zhao, Z., Jin, X.Q., Bai, Z.J.: A geometric nonlinear conjugate gradient method for stochastic inverse eigenvalue problems[J]. SIAM J. Numer. Anal. 54(4), 2015–2035 (2016)
Funding
The research was supported in part by the National Natural Science Foundation of China (11761024,12071159,11671158, U1811464, 11561015,11961012), Natural Science Foundation of Guangxi Province (2016GXNSFAA380074, 2016GXNSFFA380009, 2017GXNSFBA198082), and NSF-DMS 1419028 of the United States.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Raymond H. Chan
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Proof of Lemma 2.2
Proof
We establish the proof of Lemma 2.2 step by step.
-
For \(M\in \mathbb {C}^{m\times n}\),
$$ \begin{array}{l} \!\vec({M^{H}})\!\cong\! \vec(\widetilde{M^{H}}) = \begin{bmatrix}\vec(\Re(M)^{T})\\ -\vec(\Im(M)^{T})\end{bmatrix} = \begin{bmatrix}T_{(n,m)}&0\\ 0& -T_{(n,m)}\end{bmatrix}\begin{bmatrix}\vec(\Re(M))\\ \vec(\Im(M))\end{bmatrix}. \end{array} $$ -
For \(M\in \mathbb {C}^{n\times n}\),
$$ \begin{array}{rl} \vec(\operatorname{skewH}(M))\cong \vec(\widetilde{\operatorname{skewH}(M)})=&\frac{1}{2}\vec(\widetilde{M-M^{H}})\\ =&\frac{1}{2}\begin{bmatrix}\vec(\Re(M))-\vec(\Re(M)^{T})\\ \vec(\Im(M))+\vec(\Im(M)^{T})\end{bmatrix}\\ =&\begin{bmatrix}\frac{1}{2}(I_{n^{2}}-T_{(n,n)})&0\\ 0& \frac{1}{2}(I_{n^{2}}+T_{(n,n)})\end{bmatrix}\\ &\begin{bmatrix}\vec(\Re(M))\\ \vec(\Im(M))\end{bmatrix}. \end{array} $$ -
For \(M\in \mathbb {AH}^{n\times n}\), by MH = −M, we have R(M)T = −R(M) and I(M)T = I(M). Thus, from Lemma 2.1, one can get
$$ \begin{array}{rl} \vec(M)\cong \vec(\widetilde{M})=& \begin{bmatrix}\vec(\Re(M))\\ \vec(\text{Im}(M))\end{bmatrix} =\begin{bmatrix} K_{n}\text{vec}_{K}(\Re(M))\\ S_{n}\text{vec}_{S}(\text{Im}(M)) \end{bmatrix}\\ =&\begin{bmatrix}K_{n}&0\\ 0& S_{n} \end{bmatrix} \begin{bmatrix} \text{vec}_{K}(\Re(M))\\ \text{vec}_{S}(\text{Im}(M)) \end{bmatrix}. \end{array} $$ -
By using the fact that \(\vec (\Re (X))=\Re (\vec (X))\) and \(\vec (\text {Im}(X))= \Re (\vec (X))\) for any \(X\in \mathbb {C}^{n\times s}\), we have
$$ \begin{array}{rl} \vec(MXN)&=(N^{T}\otimes M)\vec(X)\\ &=\Big(\Re(N^{T}\!\otimes\! M) + i\text{Im}(N^{T}\!\otimes\! M)\Big) \Big(\Re(\vec(X)) + i\Im(\vec(X))\Big)\\ &=\Re(N^{T}\otimes M)\Re(\vec(X))-\text{Im}(N^{T}\otimes M)\text{Im}(\vec(X))\\ &+i\Big(\Re(N^{T}\otimes M)\text{Im}(\vec(X))+ \text{Im}(N^{T}\otimes M)\Re(\vec(X)) \Big)\\ &=\Big[\Re(N^{T}\otimes M)~~\ -\text{Im}(N^{T}\otimes M)\Big]\begin{bmatrix}\Re(\vec(X))\\ \text{Im}(\vec(X))\end{bmatrix}\\ &+i\Big[\text{Im}(N^{T}\otimes M)~~ \Re(N^{T}\otimes M)\Big]\begin{bmatrix}\Re(\vec(X))\\ \text{Im}(\vec(X))\end{bmatrix}\\ &=\Re\Big[ N^{T}\otimes M~~\ i(N^{T}\otimes M)\Big]\begin{bmatrix}\vec(\Re(X))\\ \vec(\text{Im}(X))\end{bmatrix}\\ &+i \text{Im}\Big[ N^{T}\otimes M~~\ i(N^{T}\otimes M)\Big]\begin{bmatrix}\vec(\Re(X))\\ \vec(\text{Im}(X))\end{bmatrix}. \end{array} $$Let T = [NT ⊗ M i(NT ⊗ M)], then we get
$$ \vec(MXN)\cong \vec(\widetilde{MXN})=\begin{bmatrix}\Re(T)\\ \text{Im}(T)\end{bmatrix}\begin{bmatrix}\vec(\Re(X))\\ \vec(\text{Im}(X))\end{bmatrix}. $$Similarly, one gets
$$ \vec(MX^{H}N)\cong\vec(\widetilde{MX^{H}N})=\begin{bmatrix}\widetilde{T}_{1}\\ \widetilde{T}_{2}\end{bmatrix}\begin{bmatrix}\vec(\Re(X))\\ \vec(\text{Im}(X))\end{bmatrix}, $$where
$$\widetilde{T}=\Big[ (N^{T}\otimes M)T_{(n,s)}~~\ -i(N^{T}\otimes M)T_{(n,s)}\Big],\ \ \ \widetilde{T}_{1}=\Re(\widetilde{T}),\ \ \ \widetilde{T}_{2}=\text{Im}(\widetilde{T}).$$ -
For any \(X=\Re (X)+i\text {Im}(X)\in \mathbb {AH}^{n\times n}\), it is easy to see that
$$X\in \mathbb{AH}^{n\times n}\Leftrightarrow \begin{bmatrix}\Re(X)^{T}\\ \text{Im}(X)^{T}\end{bmatrix}=\begin{bmatrix}-\Re(X)\\ \text{Im}(X)\end{bmatrix}.$$Then, together with Lemma 2.1, for \(M\in \mathbb {C}^{m\times n}\), \(X\in \mathbb {AH}^{n\times n}\), and \(C\in \mathbb {C}^{n\times t}\), one gets
$$ \vec(MXN)\cong\vec(\widetilde{MXN})=\begin{bmatrix}W_{1}\\ W_{2}\end{bmatrix}\begin{bmatrix}\text{vec}_{K}(\Re(X))\\ \text{vec}_{S}(\text{Im}(X))\end{bmatrix}, $$where
$$ W=\Big[ (N^{T}\otimes M)K_{n}~~\ i(N^{T}\otimes M)S_{n}\Big],\ \ \ W_{1}=\Re(W),\ \ \ W_{2}=\text{Im}(W). $$
□
Representation matrix H A of the Hessian Hess f(V,P)
The following theorem write out the representation matrix HA of the Hessian Hess f(V,P) of the objective function with respect to a certain basis of the tangent space. The representation matrix HA has 32 blocks and all of them are computed and explicitly described in detail.
Theorem 7.1
Let H be a linear transformation on \(\mathbb {R}^{K}\) that acts as
where EH, FH, MH, and NH are given in Eqs. 3.36–3.39. Then, the representation matrix HA of H is given by
where
and where
Proof
Let QE, QF, QM, and QN be defined as in Eq. 5.9 and noting that EH, Ex and Mx are all l-by-l skew-Hermitian matrices. From Eqs. 2.10 and 2.11, together with Lemma 2.2, \(\vec (E_{H})\cong \vec (\widetilde {E_{H}})\) with EH given in Eq. 3.36 can be calculated as follows:
Following from the fact that \({K_{l}^{T}}K_{l}=I_{\frac {n(n-1)}{2}}\), \({S_{l}^{T}}S_{l}=I_{\frac {n(n+1)}{2}}\) in Lemma 2.1, and the definitions of QE,1, QE,2, QF,1, QF,2, QM,1, QM,2, QN,1 and QN,2 in Eq. 5.5, we have
Similarly, from Eqs. 3.37, 5.11 and 5.6, \(\vec (F_{H})\cong \vec (\widetilde {F_{H}})\) can be calculated as
Based on the same analogy as used for the derivation of \(\vec (E_{H})\) and \(\vec (F_{H})\), and noting that MH is also a l-by-l skew-Hermitian matrix, we also obtain the following equations using Eqs. 3.38, 3.39, 5.7, 5.8, 5.12 and 5.13:
This completes the proof. □
Rights and permissions
About this article
Cite this article
Li, Jf., Li, W., Duan, Xf. et al. Newton’s method for the parameterized generalized eigenvalue problem with nonsquare matrix pencils. Adv Comput Math 47, 29 (2021). https://doi.org/10.1007/s10444-021-09855-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10444-021-09855-w