A well-balanced high-order scheme on van Leer-type for the shallow water equations with temperature gradient and variable bottom topography | Advances in Computational Mathematics
Skip to main content
Springer Nature Link
Log in

A well-balanced high-order scheme on van Leer-type for the shallow water equations with temperature gradient and variable bottom topography

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

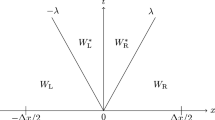
Abstract

A well-balanced high-order scheme for shallow water equations with variable topography and temperature gradient is constructed. This scheme is of van Leer-type and is based on exact Riemann solvers. The scheme is shown to be able to capture almost exactly the stationary smooth solutions as well as stationary elementary discontinuities. Numerical tests show that the scheme gives a much better accuracy than the Godunov-type scheme and can work well even in the resonant regime. Wave interaction problems are also tested where the scheme possesses a good accuracy. It turns out that the superbee limiter can provide us with more accurate approximations than van Leer’s limiter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ambroso, A., Chalons, C., Coquel, F., Galié, T.: Relaxation and numerical approximation of a two-fluid two-pressure diphasic model. Math. Mod. Numer. Anal. 43, 1063–1097 (2009)

    Article  MathSciNet  Google Scholar 

  2. Ambroso, A., Chalons, C., Raviart, P.-A.: A Godunov-type method for the seven-equation model of compressible two-phase flow. Computers & Fluids 54, 67–91 (2012)

    Article  MathSciNet  Google Scholar 

  3. Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., Perthame, B.: A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci Comput. 25, 2050–2065 (2004)

    Article  MathSciNet  Google Scholar 

  4. Baudin, M., Coquel, F., Tran, Q.-H.: A semi-implicit relaxation scheme for modeling two-phase flow in a pipeline. SIAM J. Sci. Comput. 27, 914–936 (2005)

    Article  MathSciNet  Google Scholar 

  5. Botchorishvili, R., Perthame, B., Vasseur, A.: Equilibrium schemes for scalar conservation laws with stiff sources. Math. Comput. 72, 131–157 (2003)

    Article  MathSciNet  Google Scholar 

  6. Botchorishvili, R., Pironneau, O.: Finite volume schemes with equilibrium type discretization of source terms for scalar conservation laws. J. Comput. Phys. 187, 391–427 (2003)

    Article  MathSciNet  Google Scholar 

  7. Chinnayya, A., LeRoux, A.-Y., Seguin, N.: A well-balanced numerical scheme for the approximation of the shallow water equations with topography: the resonance phenomenon. Int. J. Finite Vol. 1(4), 33 (2004)

    MathSciNet  Google Scholar 

  8. Chertock, A., Kurganov, A., Liu, Y.: Central-upwind schemes for the system of shallow water equations with horizontal temperature gradients. Num. Math. 127, 595–639 (2014)

    Article  MathSciNet  Google Scholar 

  9. Cuong, D.H., Thanh, M.D.: A well-balanced van Leer-type numerical scheme for shallow water equations with variable topography. Adv. Comput. Math. 43, 1197–1225 (2017)

    Article  MathSciNet  Google Scholar 

  10. Cuong, D.H., Thanh, M.D.: A high-resolution van Leer-type scheme for a model of fluid flows in a nozzle with variable cross-section. J. Korean Math. Soc. 54(1), 141–175 (2017)

    Article  MathSciNet  Google Scholar 

  11. Coquel, F., Hérard, J.-M., Saleh, K., Seguin, N.: Two properties of two-velocity two-pressure models for two-phase flows. Commun. Math. Sci. 12, 593–600 (2014)

    Article  MathSciNet  Google Scholar 

  12. Dal Maso, G., LeFloch, P.G., Murat, F.: Definition and weak stability of nonconservative products. J. Math. Pures Appl. 74, 483–548 (1995)

    MathSciNet  MATH  Google Scholar 

  13. Desveaux, V., Zenk, M., Berthon, C., Klingenberg, C.: Well-balanced schemes to capture non-explicit steady states: Ripa model. Math. Comp. 85, 1571–1602 (2016)

    Article  MathSciNet  Google Scholar 

  14. Gallardo, J.M., Parés, C., Castro, M.: On a well-balanced high-order finite volume scheme for shallow water equations with topography and dry areas. J. Comput. Phys. 227, 574–601 (2007)

    Article  MathSciNet  Google Scholar 

  15. Gallouet, T., Herard, J.-M., Seguin, N.: Some approximate Godunov schemes to compute shallow-water equations with topography. Comput. & Fluids 32, 479–513 (2003)

    Article  MathSciNet  Google Scholar 

  16. Godlewski, E., Raviart, P.-A.: Numerical approximation of hyperbolic systems of conservation laws springer (1996)

  17. Greenberg, J.M., Leroux, A.Y.: A well-balanced scheme for the numerical processing of source terms in hyperbolic equations. SIAM J. Numer. Anal. 33, 1–16 (1996)

    Article  MathSciNet  Google Scholar 

  18. Han, X., Li, G.: Well-balanced finite difference WENO schemes for the Ripa model. Comput. Fluids 134-135, 1–10 (2016)

    Article  MathSciNet  Google Scholar 

  19. Hou, T.Y., LeFloch, P.: Why nonconservative schemes converge to wrong solutions. Error analysis Math. of Comput. 62, 497–530 (1994)

    MathSciNet  MATH  Google Scholar 

  20. Kröner, D., Thanh, M. D.: Numerical solutions to compressible flows in a nozzle with variable cross-section. SIAM J. Numer. Anal. 43, 796–824 (2005)

    Article  MathSciNet  Google Scholar 

  21. LeFloch, P.G., Thanh, M.D.: A Godunov-type method for the shallow water equations with variable topography in the resonant regime. J. Comput. Phys. 230, 7631–7660 (2011)

    Article  MathSciNet  Google Scholar 

  22. Li, G., Caleffi, V., Qi, Z.K.: A well-balanced finite difference WENO scheme for shallow water flow model. Appl. Math. Comput. 265, 1–16 (2015)

    MathSciNet  MATH  Google Scholar 

  23. Li, G., Song, L.N., Gao, J.M.: High order well-balanced discontinuous Galerkin methods based on hydrostatic reconstruction for shallow water equations. J. Comput. Appl. Math. 340, 546–560 (2018)

    Article  MathSciNet  Google Scholar 

  24. Qian, S.G., Shao, F.J., Li, G.: High order well-balanced discontinuous Galerkin methods for shallow water flow under temperature fields. Comput. Appl. Math. 37, 5775–5794 (2018)

    Article  MathSciNet  Google Scholar 

  25. collab= P. Ripa: Conservation laws for primitive equations models with inhomogeneous layers. Geophys Astrophys Fluid Dyn. 70, 85–111 (1993)

    Article  MathSciNet  Google Scholar 

  26. Ripa, P.: On improving a one-layer ocean model with thermodynamics. J. Fluid Mech. 303, 169–201 (1995)

    Article  MathSciNet  Google Scholar 

  27. Rosatti, G., Begnudelli, L.: The Riemann Problem for the one-dimensional, free-surface shallow water equations with a bed step: theoretical analysis and numerical simulations. J. Comput. Phys. 229, 760–787 (2010)

    Article  MathSciNet  Google Scholar 

  28. Sanchez-Linares, C., Morales de Luna, T., Castro Diaz, M.J.: A HLLC scheme for Ripa model. Appl. Math. Comput. 72, 369–384 (2016)

    MathSciNet  MATH  Google Scholar 

  29. Saurel, R., Abgrall, R.: A multi-phase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150, 425–467 (1999)

    Article  MathSciNet  Google Scholar 

  30. Tian, B., Toro, E.F., Castro, C.E.: A path-conservative method for a five-equation model of two-phase flow with an HLLC-type Riemann solver. Comput. & Fluids 46, 122–132 (2011)

    Article  MathSciNet  Google Scholar 

  31. Thanh, M.D.: The Riemann problem for the shallow water equations with horizontal temperature gradients. Appl. Math. Comput. 325, 159–178 (2018)

    MathSciNet  MATH  Google Scholar 

  32. Thanh, M.D., Thanh, N.X.: Well-balanced numerical schemes for shallow water equations with horizontal temperature gradient. Bull. Malays. Math. Sci. Soc 43(1), 783–807 (2020). https://doi.org/10.1007/s40840-018-00713-5

    Article  MathSciNet  Google Scholar 

  33. Thanh, N.X., Thanh, M.D., Cuong, D.H.: Godunov-type numerical scheme for the shallow water equations with horizontal temperature gradient. Taiwan. J. Math. 24(1), 179–223 (2020). https://doi.org/10.11650/tjm/190501

    Article  MathSciNet  Google Scholar 

  34. Touma, R., Klingenberg, C.: Well-balanced central finite volume methods for the Ripa system. Appl. Num. Math. 97, 42–68 (2015)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The author would like to thank the reviewers for their very constructive comments and fruitful discussions. This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number “101.02-2019.306”.

Funding

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number “101.02-2019.306.”

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, University of Science, 227 Nguyen Van Cu str., District 5, Ho Chi Minh City, Vietnam

    Nguyen Xuan Thanh

  2. Department of Mathematics, International University, Quarter 6, Linh Trung Ward, Thu Duc District, Ho Chi Minh City, Vietnam

    Mai Duc Thanh

  3. Department of Mathematics, Ho Chi Minh City University of Pedagogy, 280 An Duong Vuong str., District 5, Ho Chi Minh City, Vietnam

    Dao Huy Cuong

  4. Vietnam National University, Ho Chi Minh City, Vietnam

    Nguyen Xuan Thanh & Mai Duc Thanh

Authors
  1. Nguyen Xuan Thanh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mai Duc Thanh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dao Huy Cuong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mai Duc Thanh.

Additional information

Communicated by: Jan Hesthaven

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Thanh, N.X., Thanh, M.D. & Cuong, D.H. A well-balanced high-order scheme on van Leer-type for the shallow water equations with temperature gradient and variable bottom topography. Adv Comput Math 47, 13 (2021). https://doi.org/10.1007/s10444-020-09832-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-020-09832-9

Keywords

Mathematics Subject Classification (2010)

Search

Navigation