Abstract
Research in psychology about reasoning has often been restricted to relatively inexpressive statements involving quantifiers (e.g. syllogisms). This is limited to situations that typically do not arise in practical settings, like ontology engineering. In order to provide an analysis of inference, we focus on reasoning tasks presented in external graphic representations where statements correspond to those involving multiple quantifiers and unary and binary relations. Our experiment measured participants’ performance when reasoning with two notations. The first notation used topological constraints to convey information via node-link diagrams (i.e. graphs). The second used topological and spatial constraints to convey information (Euler diagrams with additional graph-like syntax). We found that topo-spatial representations were more effective for inferences than topological representations alone. Reasoning with statements involving multiple quantifiers was harder than reasoning with single quantifiers in topological representations, but not in topo-spatial representations. These findings are compared to those in sentential reasoning tasks.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Middle terms appear in both major premises (containing major terms) and minor premises (containing minor terms), and minor and major terms compose conclusions.
In addition, Stenning and van Lambalgen clearly stated that “If the interpretation is not fixed, what is one actually testing? (p. 291)”.
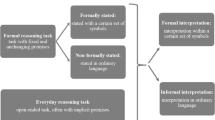
As discussed in Stenning (2002, Chap. 2), graph (node-link) representations can essentially be the same as sentential representations with respect to expressivity.
https://protegewiki.stanford.edu/wiki/SOVA (Accessed Dec. 2017)
In the paper, each class (concept) may denote an empty or non-empty set. Consequently, each minimal region (i.e. a region having no other region contained within it) in a concept diagram also may denote an empty or a non-empty set. Thus, when the relation between two curves is unknown, they are represented as two partially overlapping curves. Note that full understanding of diagrammatic semantics with respect to partially overlapping curves is not required for understanding the cognitive strategy described here. If people find that an inclusion or exclusion relationship is unspecified to be merged, they can judge the validities of arguments. Indeed, in Sato et al. (2018b) who recorded the coordinate values of diagrams as they were moved by reasoners, it was reported that some reasoners really enumerated multiple possible configurations of inclusion, exclusion, and overlapping relationships, instead of placing curves as partially overlapping.
This kind of difficulty in premise integration can also arise in reasoning with Euler diagrams in cases of syllogisms having an existential premise (e.g. All B are A; some C are B. Therefore, some C are A); see Sato and Mineshima (2015).
In statistical hypothesis testing, the null hypotheses corresponding to the above predictions are that there is no significant difference between the two conditions. While the predictions of (2), (3), and (5) indicate that the null hypotheses are expected to be rejected, the predictions of (1) and (4) indicate that the null hypotheses are not expected to be rejected. Of course, there is no rigorous method of validating that no statistically significant difference (effect) exists. However, should we find no significant difference then this, at the very least, supports our predictions (1) and (4) and, thus, allows us to discuss the nature of human inference in question here.
This is consistent with the view that diagrammatic reasoning is a kind of surrogated reasoning (Barwise and Shimojima 1995), in which reasoning about statements having semantic values is partially taken over by operations on external aids such as diagrams (for various examples of diagrammatic reasoning, see Glasgow et al. 1995). Notions related to surrogation have also been discussed as analogical mapping in Gentner et al. (2001), Funt (1980), Steels (1990), and Chandrasekaran (2011).
For example, errors caused by the misinterpretation of premises should be prevented here, as discussed in the Introduction.
References
Barwise J, Shimojima A (1995) Surrogate reasoning. Cogn Stud Bull Jpn Cogn Sci Soc 4:7–27
Bowman SR, Angeli G, Potts C, Manning CD (2015) A large annotated corpus for learning natural language inference. In: Proceedings of 2015 conference on empirical methods in natural language processing. The Association for Computational Linguistics, pp 632–642
Brachman RJ, Schmolze JG (1985) An overview of the KL-ONE knowledge representation system. Cogn Sci 9:171–216
Braine MDS (1998) Steps toward a mental-predicate logic. In: Braine MDS, O’Brien DP (eds) Mental logic. Lawrence Erlbaum, Mahwah, pp 273–331
Bucciarelli M, Johnson-Laird PN (1999) Strategies in syllogistic reasoning. Cogn Sci 23:247–303
Chandrasekaran B (2011) When is a bunch of marks on paper a diagram? Diagrams as homomorphic representations. Semiotica 186:69–87
Dagan I, Dolan B, Magnini B, Roth D (2009) Recognizing textual entailment: rational, evaluation and approaches. Nat Lang Eng 15(4):i–xvii
Flouris G, Huang Z, Pan JZ, Plexousakis D, Wache H (2006) Inconsistencies, negations and changes in ontologies. In: Proceedings of the 21st national conference on artificial intelligence. The AAAI Press, Menlo Park, pp 1295–1300
Funt BV (1980) Problem-solving with diagrammatic representations. Artif Intell 13:201–230
Gentner D, Holyoak KJ, Kokinov BN (eds) (2001) The analogical mind: perspectives from cognitive science. MIT Press, Cambridge
Geurts B, Van der Slik F (2005) Monotonicity and processing load. J Semant 22:97–117
Glasgow J, Narayanan NH, Chandrasekaran B (eds) (1995) Diagrammatic reasoning: cognitive and computational perspectives. MIT Press, Cambridge
Greene SB (1992) Multiple explanations for multiply quantified sentences: Are multiple models necessary? Psychol Rev 99:184–187
Harel D (1988) On visual formalisms. Commun ACM 31:514–530
Hartley RT, Barnden JA (1997) Semantic networks: visualizations of knowledge. Trends Cogn Sci 1:169–175
Itzik N, Reinhartz-Berger I (2014) SOVA—a tool for semantic and ontological variability analysis. In: Proceedings of CAiSE 2014 forum at the 26th international conference on advanced information systems engineering, CEUR, vol 1164, pp 177–184
Johnson-Laird PN, Byrne RM, Tabossi P (1989) Reasoning by model: the case of multiple quantification. Psychol Rev 96:658–673
Khemlani S, Johnson-Laird PN (2012) Theories of the syllogism: a meta-analysis. Psychol Bull 138:427–457
Khemlani S, Lotstein M, Johnson-Laird P (2014) A mental model theory of set membership. In: Proceedings of the 36th annual conference of the cognitive science society. Cognitive Science Society, Austin, TX, pp 2489–2494
Kroger JK, Nystrom LE, Cohen JD, Johnson-Laird PN (2008) Distinct neural substrates for deductive and mathematical processing. Brain Res 1243:86–103
Mascarenhas S, Koralus P (2017) Illusory inferences with quantifiers. Think Reason 23:33–48
Nguyen TAT, Power R, Piwek P, Williams S (2012) Measuring the understandability of deduction rules for OWL. In: Proceedings of the 1st international workshop on debugging ontologies and ontology mappings, LECP 79, Linköping University Electronic Press, pp 1–12
Nguyen TAT, Power R, Piwek P, Williams S (2013) Predicting the understandability of OWL inferences. In: Proceedings of the extended semantic web conference 2013, LNCS 7882. Springer, Heidelberg, pp 109–123
Politzer G, Mercier H (2008) Solving categorical syllogisms with singular premises. Think Reason 14:434–454
Politzer G, Bosc-Miné C, Sander E (2017) Preadolescents solve natural syllogisms proficiently. Cogn Sci 41:1031–1061
Ragni M, Sonntag T (2012) Preferences and illusions in quantified spatial relational reasoning. Cogn Process 13:289–292
Ragni M, Singmann H, Steinlein EM (2014) Theory comparison for generalized quantifiers. In: Proceedings of the 36th annual conference of the cognitive science society. Cognitive Science Society, Austin, TX, pp 1222–1227
Ramakrishnan S, Vijayan A (2014) A study on development of cognitive support features in recent ontology visualization tools. Artif Intell Rev 41:595–623
Sato Y, Mineshima K (2015) How diagrams can support syllogistic reasoning: an experimental study. J Logic Lang Inf 24:409–455
Sato Y, Mineshima K (2016) Human reasoning with proportional quantifiers and its support by diagrams. In: Proceedings of diagrams 2016, LNCS 9781. Springer, Switzerland, pp 123–138
Sato Y, Stapleton G, Jamnik M, Shams Z, Blake A (2017) How Network-based and set-based visualizations aid consistency checking in ontologies. In: Proceedings of the 10th international symposium on visual information communication and interaction. ACM, New York, NY, pp 137–141
Sato Y, Sugimoto Y, Ueda K (2018a) Real objects can impede conditional reasoning but augmented objects do not. Cogn Sci 42:691–707
Sato Y, Wajima Y, Ueda K (2018b) Strategy analysis of non-consequence inference with Euler diagrams. J Logic Lang Inf 27:61–77
Schmidt-Schauß M, Smolka G (1991) Attributive concept descriptions with complements. Artif Intell 48:1–26
Stapleton G, Compton M, Howse J (2017) Visualizing OWL 2 using diagrams. In: Proceedings of 2017 IEEE symposium on visual languages and human-centric computing. IEEE Computer Society Press, Los Alamitos, CA, pp 245–253
Steels L (1990) Exploiting analogical representations. Robot Auton Syst 6:71–88
Stenning K (2002) Seeing reason: image and language in learning to think. Oxford University Press, Oxford
Stenning K, Oberlander J (1995) A cognitive theory of graphical and linguistic reasoning: logic and implementation. Cogn Sci 19:97–140
Stenning K, van Lambalgen M (2001) Semantics as a foundation for psychology: a case study of Wason’s selection task. J Logic Lang Inf 10:273–317
Sugiyama K, Misue K (1991) Visualization of structural information: automatic drawing of compound digraphs. IEEE Trans Syst Man Cybern 21:876–892
W3C OWL Working Group (2012) OWL 2 web ontology language. Retrieved Dec 2017 from http://www.w3.org/TR/owl2-overview/
Acknowledgements
Parts of this study were presented in the 40th CogSci Conference (July, 2018) in Madison. The authors would like to thank John Howse, Andrew Blake and Ryo Takemura for cooperating on the experiments.
Funding
This research was funded by a Leverhulme Trust Research Project Grant (RPG-2016-082) for the project entitled Accessible Reasoning with Diagrams.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to declare.
Ethical approval
All procedures performed in the experiment involving human participants were in accordance with the ethical standards of the institutional and national research committee and with the 1964 Declaration of Helsinki and its later amendments.
Informed consent
Informed consent was obtained from all individual participants included in the experiment.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Sato, Y., Stapleton, G., Jamnik, M. et al. Human inference beyond syllogisms: an approach using external graphical representations. Cogn Process 20, 103–115 (2019). https://doi.org/10.1007/s10339-018-0877-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10339-018-0877-2