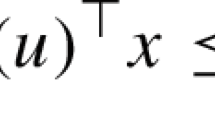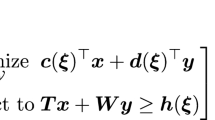Abstract
Robust optimization (RO) is a tractable method to address uncertainty in optimization problems where uncertain parameters are modeled as belonging to uncertainty sets that are commonly polyhedral or ellipsoidal. The two most frequently described methods in the literature for solving RO problems are reformulation to a deterministic optimization problem or an iterative cutting-plane method. There has been limited comparison of the two methods in the literature, and there is no guidance for when one method should be selected over the other. In this paper we perform a comprehensive computational study on a variety of problem instances for both robust linear optimization (RLO) and robust mixed-integer optimization (RMIO) problems using both methods and both polyhedral and ellipsoidal uncertainty sets. We consider multiple variants of the methods and characterize the various implementation decisions that must be made. We measure performance with multiple metrics and use statistical techniques to quantify certainty in the results. We find for polyhedral uncertainty sets that neither method dominates the other, in contrast to previous results in the literature. For ellipsoidal uncertainty sets we find that the reformulation is better for RLO problems, but there is no dominant method for RMIO problems. Given that there is no clearly dominant method, we describe a hybrid method that solves, in parallel, an instance with both the reformulation method and the cutting-plane method. We find that this hybrid approach can reduce runtimes to 50–75 % of the runtime for any one method and suggest ways that this result can be achieved and further improved on.



Similar content being viewed by others
References
Ben-Tal A, El Ghaoui, L, Nemirovski A (2009) Robust optimization. Princeton University Press, Princeton
Ben-Tal A, Nemirovski A (1999) Robust solutions of uncertain linear programs. Oper Res Lett 25(1):1–13
Ben-Tal A, Nemirovski A (2000) Robust solutions of linear programming problems contaminated with uncertain data. Math Program 88:411–424
Bertsimas D, Brown DB, Caramanis C (2011) Theory and applications of robust optimization. SIAM Rev 53(3):464–501
Bertsimas D, Sim M (2004) The price of robustness. Oper Res 52(1):35–53
Bixby R, Ceria S, McZeal C, Savelsberg M (1998) An updated mixed integer programming library: MIPLIB 3.0. Optima 58:12–15
Briant O, Lemarchal C, Meurdesoif P, Michel S, Perrot N, Vanderbeck F (2008) Comparison of bundle and classical column generation. Math Program 113(2):299–344
Carvajal R, Ahmed S, Nemhauser G, Furman K, Goel V, Shao Y (2014) Using diversification, communication and parallelism to solve mixed-integer linear programs. Oper Res Lett 42(2):186–189
Dolan ED, Moré JJ (2002) Benchmarking optimization software with performance profiles. Math Program 91:201–213
Efron B, Tibshirani RJ (1994) An introduction to the bootstrap, vol. 57. CRC Press, USA
Fischetti M, Monaci M (2012) Cutting plane versus compact formulations for uncertain (integer) linear programs. Math Program Comput 4:239–273
Fleming PJ, Wallace JJ (1986) How not to lie with statistics: the correct way to summarize benchmark results. Commun ACM 29(3):218–221
Gay DM (1985) Electronic mail distribution of linear programming test problems. Math Program Soc COAL Newsl 13:10–12
Goh J, Sim M (2011) Robust optimization made easy with rome. Oper Res 59(4):973–985
Gurobi Optimization Inc. (2014) Gurobi optimizer reference manual. http://www.gurobi.com. Accessed 1 June 2014
Koch T, Achterberg T, Andersen E, Bastert O, Berthold T, Bixby RE, Danna E, Gamrath G, Gleixner AM, Heinz S, Lodi A, Mittelmann H, Ralphs T, Salvagnin D, Steffy DE, Wolter K (2011) MIPLIB 2010. Math Program Comput 3(2):103–163
Koch T, Ralphs T, Shinano Y (2012) Could we use a million cores to solve an integer program? Math Methods Oper Res 76(1):67–93
Mittelmann H (2015) Benchmark of parallel LP solvers. http://plato.asu.edu/ftp/lpcom.html. Accessed 1 Mar 2015
Mutapcic A, Boyd S (2009) Cutting-set methods for robust convex optimization with pessimizing oracles. Optim Methods Softw 24(3):381–406
Zverovich V, Fbin C, Ellison E, Mitra G (2012) A computational study of a solver system for processing two-stage stochastic LPs with enhanced benders decomposition. Math Program Comput 4(3):211–238
Acknowledgments
The authors would like to thank the two anonymous reviewers for their help in improving the rigour and focus of the paper. This research was partially supported by ONR Grant N00014-12-1-0999. M. Lubin was supported by the DOE Computational Science Graduate Fellowship, which is provided under Grant No. DE-FG02-97ER25308.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bertsimas, D., Dunning, I. & Lubin, M. Reformulation versus cutting-planes for robust optimization. Comput Manag Sci 13, 195–217 (2016). https://doi.org/10.1007/s10287-015-0236-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10287-015-0236-z