Enhancement of Non-Linear Deep Learning Model by Adjusting Confounding Variables for Bone Age Estimation in Pediatric Hand X-rays | Journal of Imaging Informatics in Medicine
Skip to main content
Springer Nature Link
Log in

Enhancement of Non-Linear Deep Learning Model by Adjusting Confounding Variables for Bone Age Estimation in Pediatric Hand X-rays

  • Published:
Journal of Digital Imaging Aims and scope Submit manuscript

Abstract

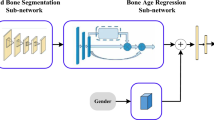
In medicine, confounding variables in a generalized linear model are often adjusted; however, these variables have not yet been exploited in a non-linear deep learning model. Sex plays important role in bone age estimation, and non-linear deep learning model reported their performances comparable to human experts. Therefore, we investigate the properties of using confounding variables in a non-linear deep learning model for bone age estimation in pediatric hand X-rays. The RSNA Pediatric Bone Age Challenge (2017) dataset is used to train deep learning models. The RSNA test dataset is used for internal validation, and 227 pediatric hand X-ray images with bone age, chronological age, and sex information from Asan Medical Center (AMC) for external validation. U-Net based autoencoder, U-Net multi-task learning (MTL), and auxiliary-accelerated MTL (AA-MTL) models are chosen. Bone age estimations adjusted by input, output prediction, and without adjusting the confounding variables are compared. Additionally, ablation studies for model size, auxiliary task hierarchy, and multiple tasks are conducted. Correlation and Bland–Altman plots between ground truth and model-predicted bone ages are evaluated. Averaged saliency maps based on image registration are superimposed on representative images according to puberty stage. In the RSNA test dataset, adjusting by input shows the best performances regardless of model size, with mean average errors (MAEs) of 5.740, 5.478, and 5.434 months for the U-Net backbone, U-Net MTL, and AA-MTL models, respectively. However, in the AMC dataset, the AA-MTL model that adjusts the confounding variable by prediction shows the best performance with an MAE of 8.190 months, whereas the other models show the best performances by adjusting the confounding variables by input. Ablation studies of task hierarchy reveal no significant differences in the results of the RSNA dataset. However, predicting the confounding variable in the second encoder layer and estimating bone age in the bottleneck layer shows the best performance in the AMC dataset. Ablations studies of multiple tasks reveal that leveraging confounding variables plays an important role regardless of multiple tasks. To estimate bone age in pediatric X-rays, the clinical setting and balance between model size, task hierarchy, and confounding adjustment method play important roles in performance and generalizability; therefore, proper adjusting methods of confounding variables to train deep learning-based models are required for improved models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availability

The RSNA dataset is publicly available at: https://www.rsna.org/education/ai-resources-and-training/ai-image-challenge/rsna-pediatric-bone-age-challenge-2017.

References

  1. Goodfellow, I., Y. Bengio, and A. Courville, Deep learning. 2016: MIT press.

  2. Szegedy, C., et al. Going deeper with convolutions. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2015.

  3. He, K., et al. Deep residual learning for image recognition. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.

  4. Raghu, V.K., et al., Deep learning to estimate biological age from chest radiographs. JACC: Cardiovascular Imaging, 2021. 14(11): p. 2226–2236.

  5. Korot, E., et al., Predicting sex from retinal fundus photographs using automated deep learning. Scientific reports, 2021. 11(1): p. 1-8.

    Article  Google Scholar 

  6. Wu, L., et al., Effect of a deep learning-based system on the miss rate of gastric neoplasms during upper gastrointestinal endoscopy: a single-centre, tandem, randomised controlled trial. 2021. 6(9): p. 700–708.

  7. Rajpurkar, P., et al., Deep learning for chest radiograph diagnosis: A retrospective comparison of the CheXNeXt algorithm to practicing radiologists. 2018. 15(11): p. e1002686.

    Google Scholar 

  8. Nelder, J.A. and R.W.J.J.o.t.R.S.S.S.A. Wedderburn, Generalized linear models. 1972. 135(3): p. 370–384.

  9. Robinson, L.D., et al., The effects of covariate adjustment in generalized linear models. 1998. 27(7): p. 1653-1675.

    Google Scholar 

  10. Shpitser, I., T. VanderWeele, and J.M.J.a.p.a. Robins, On the validity of covariate adjustment for estimating causal effects. 2012.

  11. Pourhoseingholi, M.A., et al., How to control confounding effects by statistical analysis. 2012. 5(2): p. 79.

    Google Scholar 

  12. Kahlert, J., et al., Control of confounding in the analysis phase–an overview for clinicians. 2017. 9: p. 195.

  13. McPherson, S., et al., Age as a confounding factor for the accurate non-invasive diagnosis of advanced NAFLD fibrosis. 2017. 112(5): p. 740.

    Google Scholar 

  14. Wu, A.H., et al., Association of obesity and survival in systolic heart failure after acute myocardial infarction: potential confounding by age. 2010. 12(6): p. 566-573.

    Google Scholar 

  15. Reeves, M.J. and L.D.J.N. Lisabeth, The confounding issue of sex and stroke. 2010. 74(12): p. 947-948.

    Google Scholar 

  16. Young, R.P., et al., COPD prevalence is increased in lung cancer, independent of age, sex and smoking history. 2009. 34(2): p. 380–386.

  17. Tanner, J., et al., Prediction of adult height from height and bone age in childhood. A new system of equations (TW Mark II) based on a sample including very tall and very short children. Archives of disease in childhood, 1983. 58(10): p. 767–776.

  18. Tanner, J., et al., Prediction of adult height from height, bone age, and occurrence of menarche, at ages 4 to 16 with allowance for midparent height. Archives of disease in childhood, 1975. 50(1): p. 14-26.

    Article  CAS  PubMed Central  PubMed  Google Scholar 

  19. Gkourogianni, A., et al., Clinical characterization of patients with autosomal dominant short stature due to aggrecan mutations. 2017. 102(2): p. 460-469.

    Google Scholar 

  20. Rosenfeld, R.G., et al., Diagnostic controversy: the diagnosis of childhood growth hormone deficiency revisited. The Journal of Clinical Endocrinology & Metabolism, 1995. 80(5): p. 1532-1540.

    CAS  Google Scholar 

  21. KAPLAN, S.L. and M.M. GRUMBACH, CLINICAL REVIEW 14 Pathophysiology and Treatment of Sexual Precocity. The Journal of Clinical Endocrinology & Metabolism, 1990. 71(4): p. 785–789.

  22. Allen, D.B., Growth suppression by glucocorticoid therapy. Endocrinology and metabolism clinics of North America, 1996. 25(3): p. 699-717.

    Article  CAS  PubMed  Google Scholar 

  23. Vasseur, F., et al., Nutritional status and growth in pediatric Crohn's disease: a population-based study. Official journal of the American College of Gastroenterology| ACG, 2010. 105(8): p. 1893–1900.

  24. de Zegher, F., et al., Growth failure in children with systemic juvenile idiopathic arthritis and prolonged inflammation despite treatment with biologicals: Late normalization of height by combined hormonal therapies. Hormone Research in Paediatrics, 2018. 90(5): p. 337-343.

    Article  PubMed  Google Scholar 

  25. Thommessen, M., A. Heiberg, and B. Kase, Feeding problems in children with congenital heart disease: the impact on energy intake and growth outcome. European journal of clinical nutrition, 1992. 46(7): p. 457-464.

    CAS  PubMed  Google Scholar 

  26. Halabi, S.S., et al., The RSNA pediatric bone age machine learning challenge. 2019. 290(2): p. 498.

    Google Scholar 

  27. Beheshtian, E., et al., Generalizability and bias in a deep learning pediatric bone age prediction model using hand radiographs. 2022: p. 220505.

  28. Arisaka, O., et al., Preliminary report: effect of adrenal androgen and estrogen on bone maturation and bone mineral density. 2001. 50(4): p. 377-379.

    CAS  Google Scholar 

  29. Larson, D.B., et al., Performance of a deep-learning neural network model in assessing skeletal maturity on pediatric hand radiographs. 2018. 287(1): p. 313-322.

    Google Scholar 

  30. Greulich, W.W. and S.I. Pyle, Radiographic atlas of skeletal development of the hand and wrist. 1959: Stanford university press.

  31. Kim, K.D., et al., Enhancing deep learning based classifiers with inpainting anatomical side markers (L/R markers) for multi-center trials. 2022. 220: p. 106705.

  32. Ronneberger, O., P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. in International Conference on Medical image computing and computer-assisted intervention. 2015. Springer.

  33. Selvaraju, R.R., et al. Grad-cam: Visual explanations from deep networks via gradient-based localization. in Proceedings of the IEEE international conference on computer vision. 2017.

  34. Cohen, P., et al., Consensus statement on the diagnosis and treatment of children with idiopathic short stature: a summary of the Growth Hormone Research Society, the Lawson Wilkins Pediatric Endocrine Society, and the European Society for Paediatric Endocrinology Workshop. 2008. 93(11): p. 4210–4217.

  35. De Onis, M., et al., Comparison of the WHO child growth standards and the CDC 2000 growth charts. 2007. 137(1): p. 144–148.

  36. De Onis, M., et al., Worldwide implementation of the WHO child growth standards. 2012. 15(9): p. 1603-1610.

    Google Scholar 

  37. Altman, D.G. and J.M.J.J.o.t.R.S.S.S.D. Bland, Measurement in medicine: the analysis of method comparison studies. 1983. 32(3): p. 307–317.

  38. Bland, J.M. and D.J.T.l. Altman, Statistical methods for assessing agreement between two methods of clinical measurement. 1986. 327(8476): p. 307–310.

  39. He, K., et al., Masked autoencoders are scalable vision learners. 2021.

  40. DeVries, T. and G.W.J.a.p.a. Taylor, Improved regularization of convolutional neural networks with cutout. 2017.

  41. Standley, T., et al. Which tasks should be learned together in multi-task learning? in International Conference on Machine Learning. 2020. PMLR.

  42. Misra, I., et al. Cross-stitch networks for multi-task learning. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.

  43. Zhang, A., et al., Racial differences in growth patterns of children assessed on the basis of bone age. 2009. 250(1): p. 228-235.

    Google Scholar 

  44. Escobar, M., et al. Hand pose estimation for pediatric bone age assessment. in International conference on medical image computing and computer-assisted intervention. 2019. Springer.

  45. Lee, H., et al., Fully automated deep learning system for bone age assessment. 2017. 30(4): p. 427-441.

    Google Scholar 

  46. Pan, I., et al., Improving automated pediatric bone age estimation using ensembles of models from the 2017 RSNA machine learning challenge. 2019. 1(6).

  47. Liu, R., et al., Coarse-to-fine segmentation and ensemble convolutional neural networks for automated pediatric bone age assessment. 2022. 75: p. 103532.

    Google Scholar 

  48. Gottschalk, M.B., M. Danilevich, and H.P.J.H. Gottschalk, Carpal coalitions and metacarpal synostoses: a review. 2016. 11(3): p. 271-277.

    Google Scholar 

  49. Pruszczynski, B., et al., Incidence of carpal coalition in the pediatric population. 2016. 36(8): p. e106-e110.

    Google Scholar 

Download references

Acknowledgements

We thank Kyungjin Cho and Jun Soo Lee for their valuable discussion.

Funding

This study was conducted by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (HI18C2383).

Author information

Author notes

  1. Hee Mang Yoon and Namkug Kim these corresponding authors contributed equally.

Authors and Affiliations

  1. Department of Convergence Medicine, University of Ulsan College of Medicine, Asan Medical Center, 88 Olympic-Ro 43-Gil, Songpa-Gu, Seoul, 05505, Republic of Korea

    Ki Duk Kim, Miso Jang & Namkug Kim

  2. Department of Biomedical Engineering, Asan Medical Institute of Convergence Science and Technology, Asan Medical Center, College of Medicine, University of Ulsan, Seoul, 05505, Republic of Korea

    Sunggu Kyung

  3. Department of Internal Medicine, University of Ulsan College of Medicine, Asan Medical Center, Seoul, 05505, Republic of Korea

    Sunghwan Ji

  4. Department of Translational Medicine, Asan Medical Center, Asan Medical Institute of Convergence Science and Technology, University of Ulsan College of Medicine, Seoul, 05505, Republic of Korea

    Sunghwan Ji

  5. College of Medicine, The Catholic University of Korea, Seoul, 06591, Republic of Korea

    Dong Hee Lee

  6. Department of Radiology, University of Ulsan College of Medicine, Asan Medical Center, Seoul, 05505, Republic of Korea

    Hee Mang Yoon & Namkug Kim

Authors
  1. Ki Duk Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sunggu Kyung
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Miso Jang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sunghwan Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Dong Hee Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Hee Mang Yoon
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Namkug Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation was performed by Ki Duk Kim, Sunggu Kyung and Miso Jang. Data collection was performed by Hee Mang Yoon. Data analyses were performed by Ki Duk Kim, Sunghwan Ji, and Dong Hee Lee. The first draft of the manuscript was written by Ki Duk Kim and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Hee Mang Yoon or Namkug Kim.

Ethics declarations

Conflicts of Interest

The authors report no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 18 KB)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, K.D., Kyung, S., Jang, M. et al. Enhancement of Non-Linear Deep Learning Model by Adjusting Confounding Variables for Bone Age Estimation in Pediatric Hand X-rays. J Digit Imaging 36, 2003–2014 (2023). https://doi.org/10.1007/s10278-023-00849-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10278-023-00849-2

Keywords

Search

Navigation