Stochastic modeling of chemical–mechanical coupling in striated muscles

Abstract

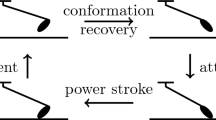
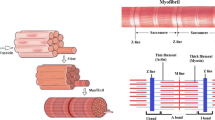
We propose a chemical–mechanical model of myosin heads in sarcomeres, within the classical description of rigid sliding filaments. In our case, myosin heads have two mechanical degrees-of-freedom (dofs)—one of which associated with the so-called power stroke—and two possible chemical states, i.e., bound to an actin site or not. Our major motivations are twofold: (1) to derive a multiscale coupled chemical–mechanical model and (2) to thus account—at the macroscopic scale—for mechanical phenomena that are out of reach for classical muscle models. This model is first written in the form of Langevin stochastic equations, and we are then able to obtain the corresponding Fokker–Planck partial differential equations governing the probability density functions associated with the mechanical dofs and chemical states. This second form is important, as it allows to monitor muscle energetics and also to compare our model with classical ones, such as the Huxley’57 model to which our equations are shown to reduce under two different types of simplifying assumptions. This provides insight and gives a Langevin form for Huxley’57. We then show how we can calibrate our model based on experimental data—taken here for skeletal muscles—and numerical simulations demonstrate the adequacy of the model to represent complex physiological phenomena, in particular the fast isometric transients in which the power stroke is known to have a crucial role, thus circumventing a limitation of many classical models.

A Summary of the main symbols used in the paper

Symbol	Definition	First occurrence
$X^t$	Location of the head tip	p. 4
$Y^t$	Internal dof of the head (power stroke)	p. 4
$s$	Position of the nearest actin binding site	p. 4
$\alpha ^t$	attachment state of the head (0 or 1)	p. 4
${\dot{x}}_{c}$	Relative velocity of actin filament	p.4
$u_{\alpha }$, $w_\alpha$, $u_{e}$	Energy of a myosin head in state $\alpha$ ($w_\alpha (x,y) = u_{\alpha }(y) + u_{e}(x+y)$)	p. 4
$\eta _x$, $\eta _y$, $\eta$	Drag coefficients	p .4
$D$	Diffusion coefficient	(2)
$P_{\alpha }(s,t)$	Probability to be attached ($\alpha =1$) or detached ($\alpha =0$)	p. 5, (5)
$p(x,y,\alpha ;s,t)$	Probability function for $(x,y,\alpha )$ (densities in (x, y), discrete in $\alpha$)	p. 5, (8)
${\overline{p}}(y;s,t)$	Effective density in the attached state	(8)
$k_{\pm }$	Attachment ($k_{+}$) and detachment ($k_{-}$) rates	(4)
$f$, $g$	Overall attachment ($f$) and detachment ($g$) functions	(20), (21)
$\mu _\alpha$	Chemical potentials for each state	(22), (23)
F	Free energy	(24)
${\dot{S}}_{prod}$	Entropy production rate	p. 8
$\tau _{c}$	Average active tension	(25)
${\overline{J}}_{1}^{0}$	Flux of the detachment reaction	(26)
$\mu _{T}$	Chemical potential of ATP	p. 8
$p^{th}_\alpha$	Density functions within the thermal equilibrium hypothesis	(34)
$f^{th}$, $g^{th}$	Overall attachment and detachment function within the thermal equilibrium hypothesis	(36a), (36b)
$T_c$	Active tension under assumptions on thermal equilibrium and on $f+g$	p. 10
$K_c$	Active stiffness under assumptions on thermal equilibrium and on $f+g$	p. 10
${\dot{e}}_{c}$	Extension rate of sarcomere	p. 10
$\tau _c^{th}$	Average tension generated by the attached cross-bridges within the thermal equilibrium hypothesis	(46)
$\check{P}_{1}^{th}$	Probability to be attached within the thermal equilibrium hypothesis, in isometric condition	(43)
$\check{n}_{1}^{th}$	Fraction of attached heads within the thermal equilibrium hypothesis, in isometric condition	(44)
$\check{\tau }_c^{th}$	Average tension within the thermal equilibrium hypothesis, in isometric condition	(45)
$T_0$	Isometric tension	(48)
$K_0$	Isometric stiffness	(48)
$T_{1}$	Tension reached at the end of a length step	(49)
$T_{2}$	Tension reached after the fast isometric transient following a length step	(50)