Abstract
We study projection-free methods for constrained Riemannian optimization. In particular, we propose a Riemannian Frank-Wolfe (RFW) method that handles constraints directly, in contrast to prior methods that rely on (potentially costly) projections. We analyze non-asymptotic convergence rates of RFW to an optimum for geodesically convex problems, and to a critical point for nonconvex objectives. We also present a practical setting under which RFW can attain a linear convergence rate. As a concrete example, we specialize RFW to the manifold of positive definite matrices and apply it to two tasks: (i) computing the matrix geometric mean (Riemannian centroid); and (ii) computing the Bures-Wasserstein barycenter. Both tasks involve geodesically convex interval constraints, for which we show that the Riemannian “linear” oracle required by RFW admits a closed form solution; this result may be of independent interest. We complement our theoretical results with an empirical comparison of RFW against state-of-the-art Riemannian optimization methods, and observe that RFW performs competitively on the task of computing Riemannian centroids.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study the following constrained optimization problem
where \(\phi : \mathcal {M}\rightarrow \mathbb {R}\) is a differentiable function and \(\mathcal {X}\) is a compact geodesically convex (henceforth, g-convex) subset of a Riemannian manifold \(\mathcal {M}\). The objective \(\phi \) may be g-convex or nonconvex. When the constraint set \(\mathcal {X}\) is “simple” one may solve (1) via Riemannian projected-gradient. But in many cases, projection onto \(\mathcal {X}\) can be expensive to compute, motivating us to seek projection-free methods.
Euclidean (\(\mathcal {M}\equiv \mathbb {R}^n\)) projection-free methods based on the Frank-Wolfe (FW) scheme [20] have recently witnessed a surge of interest in machine learning and related fields [29, 36]. Instead of projection, such FW methods rely on access to a “linear” oracle, that is, a subroutine that solves the problem
which can sometimes be much simpler than projection onto \(\mathcal {X}\). This attractive property of FW methods has been exploited in convex [2, 29], nonconvex [35], submodular [12, 21], and stochastic [24, 52] optimization problems; among others.
But as far as we are aware, FW methods have not been studied for Riemannian manifolds. Our work fills this gap in the literature by developing, analyzing, and experimenting with Riemannian Frank-Wolfe (RFW) methods. In addition to adapting FW to the Riemannian setting, there is one more challenge that we must overcome: RFW requires access to a Riemannian analog of the linear oracle (2), which can be hard even for g-convex problems.
Therefore, to complement our theoretical analysis of RFW, we discuss in detail practical settings that admit efficient Riemannian “linear” oracles. Specifically, we discuss problems where \(\mathcal {M}=\mathbb {P}_d\), the manifold of (Hermitian) positive definite matrices, and \(\mathcal {X}\) is a g-convex semidefinite interval; then problem (1) assumes the form
where L and U are positive definite matrices. An important instance of (3) is the following g-convex optimization problem (see §4 for details and notation):
which computes the Riemannian centroid of a set of positive definite matrices (also known as the “matrix geometric mean” and the “Karcher mean”) [5, 32, 37]. We will show that RFW offers a simple approach for solving (4) that performs competitively against recently published state-of-the-art Riemannian approaches. As a second application, we show that RFW allows for an efficient computation of Bures-Wasserstein barycenters on the Gaussian density manifold.
Summary of results. The key contributions of this paper are as follows:
-
1.
We introduce a Riemannian Frank-Wolfe (RFW) algorithm for addressing constrained g-convex optimization on Riemannian manifolds. We show that RFW attains a non-asymptotic O(1/k) rate of convergence to the optimal objective value, k being the number of iterations (Theorem 1). Furthermore, under additional assumptions on the objective function and the constraints, we show that RFW can even attain linear convergence rates (Theorem 2). In the nonconvex case, RFW attains a non-asymptotic \(O(1/\sqrt{k})\) rate of convergence to first-order critical points (Theorem 3). These rates are comparable to the best known guarantees for the classical Euclidean Frank-Wolfe algorithm [29, 36].
-
2.
While the Euclidean “linear” oracle is a convex problem, the Riemannian “linear” oracle is nonconvex. Therefore, the key challenge of developing RFW lies in efficiently solving the “linear” oracle. We address this problem with the following contributions:
-
We specialize RFW for g-convex problems of the form (3) on the manifold of Hermitian positive definite (HPD) matrices. Importantly, for this problem we develop a closed-form solution to the Riemannian “linear” oracle, which involves solving a nonconvex semi-definite program (SDP), see Theorem 4. We then apply RFW to computing the Riemannian mean of HPD matrices. In comparison with state-of-the-art methods, we observe that RFW performs competitively. Furthermore, we implement RFW for the computation of Bures-Wasserstein barycenters on the Gaussian density manifold.
-
We show that we can recover a sublinear convergence rate, even if the Riemannian “linear” oracle can only be solved approximately, e.g., using relaxations or iterative solvers. This makes the approach applicable to a wider range of constrained optimization problems.
-
We believe that the closed-form solutions for the HPD “linear” oracle, which involve a nonconvex SDP, should be of wider interest too. A similar approach can be used to solve the Euclidean linear oracle, a convex SDP, in closed form (Appendix 1). More broadly, we hope that our results encourage others to study RFW as well as other examples of problems with efficient Riemannian “linear” oracles.
Related work. Riemannian optimization has a venerable history. The books [1, 58] provide a historical perspective as well as basic theory. The focus of these books and of numerous older works on Riemannian optimization, e.g.,[19, 25, 41, 53], is almost exclusively on asymptotic analysis. More recently, non-asymptotic convergence analysis quantifying the iteration complexity of Riemannian optimization algorithms has begun to be pursued [3, 10, 66]. Specifically, it is known that first-order methods, such as Riemannian Gradient Descent, achieve a sublinear iteration complexity. However, to the best of our knowledge, all these works either focus on unconstrained Riemannian optimization, or handle constraints via projections. In contrast, we explore constrained g-convex optimization within an abstract RFW framework, by assuming access to a Riemannian “linear” oracle. Several applications of Riemannian optimization are known, including to matrix factorization on fixed-rank manifolds [57, 59], dictionary learning [16, 56], classical optimization under orthogonality constraints [19], averages of rotation matrices [46], elliptical distributions in statistics [54, 68], and Gaussian mixture models [27]. Explicit theory of g-convexity on HPD matrices is studied in [55]. Additional related work corresponding to the Riemannian mean of HPD matrices is discussed in Sect. 4.
2 Background
We begin by noting some background and notation from Riemannian geometry. For a deeper treatment we refer the reader to [15, 31].
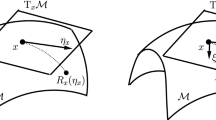
A smooth manifold \({\mathcal {M}}\) is a locally Euclidean space equipped with a differential structure. At any point \(x \in {\mathcal {M}}\), the set of tangent vectors forms the tangent space \(T_x\mathcal {M}\). Our focus is on Riemannian manifolds, i.e., smooth manifolds with a smoothly varying inner product \(\left\langle {\xi },\, {\eta } \right\rangle _x\) defined on the \(T_x\mathcal {M}\) at each point \(x\in \mathcal {M}\). We write \(\Vert \xi \Vert _x := \sqrt{\left\langle {\xi },\, {\xi } \right\rangle _x}\) for \(\xi \in T_x\mathcal {M}\); for brevity, we will drop the subscript on the norm whenever the associated tangent space is clear from context. Furthermore, we assume \(\mathcal {M}\) to be complete, which ensures that the following map is defined on the whole tangent space: We define the exponential map as a mapping from \(T_x\mathcal {M}\) to \(\mathcal {M}\) by \({{\,\mathrm{Exp}\,}}_x: T_x {\mathcal {M}} \rightarrow {\mathcal {M}}\) such that \(y={{\,\mathrm{Exp}\,}}_x(g_x) \in {\mathcal {M}}\) along a geodesic \(\gamma : [0,1] \rightarrow {\mathcal {M}}\) with \(\gamma (0)= x\), \(\gamma (1)=y\) and \({\dot{\gamma }}(0)=g_x \in T_x\mathcal {M}\). We can define an inverse exponential map \({{\,\mathrm{Exp}\,}}_x^{-1}: {\mathcal {M}} \rightarrow T_x {\mathcal {M}}\) as a diffeomorphism from the neighborhood of \(x \in {\mathcal {M}}\) onto the neighborhood of \(0 \in T_x {\mathcal {M}}\) with \({{\,\mathrm{Exp}\,}}_x^{-1}(x)=0\). Note, that the completeness of \({\mathcal {M}}\) ensures that both maps are well-defined.
Since tangent spaces are local notions, one cannot directly compare vectors lying in different tangent spaces. To tackle this issue, we use the concept of parallel transport: the idea is to transport (map) a tangent vector along a geodesic to the respective other tangent space. More precisely, let \(x, y \in {\mathcal {M}}\) with \(x \ne y\). We transport \(g_x \in T_x {\mathcal {M}}\) along a geodesic \(\gamma \) (where \(\gamma (0)=x\) and \(\gamma (1)=y\)) to the tangent space \(T_y\mathcal {M}\); we denote this by \(\varGamma _x^y g_x\). Importantly, the inner product on the tangent spaces is preserved under parallel transport, so that \(\left\langle {\xi _x},\, {\eta _x} \right\rangle _x = \left\langle {\varGamma _x^y \xi _x},\, {\varGamma _x^y \eta _x} \right\rangle _y\), where \(\xi _x, \eta _x \in T_x {\mathcal {M}}\), while \(\left\langle {\cdot },\, {\cdot } \right\rangle _x\) and \(\left\langle {\cdot },\, {\cdot } \right\rangle _y\) are the respective inner products.
2.1 Gradients, convexity, smoothness
Recall that the Riemannian gradient \({{\,\mathrm{grad}\,}}\phi (x)\) is the unique vector in \(T_x\mathcal {M}\) such that the directional derivative
When optimizing functions using gradients, it is useful to impose some added structure. The two main properties that we require are sufficiently smooth gradients and geodesic convexity. We say \(\phi : {\mathcal {M}} \rightarrow {\mathbb {R}}\) is L-smooth, or that it has L-Lipschitz gradients, if
where d(x, y) is the geodesic distance between x and y; equivalently,
We say \(\phi : {\mathcal {M}} \rightarrow {\mathbb {R}}\) is geodesically convex (g-convex) if
and call it \(\mu \)-strongly g-convex (\(\mu \ge 0\)) if
The following observation underscores the reason why g-convexity is a valuable geometric property for optimization.
Proposition 1
(Optimality) Let \(x^* \in \mathcal {X}\subset \mathcal {M}\) be a local optimum for (1). Then, \(x^*\) is globally optimal, and \(\left\langle {{{\,\mathrm{grad}\,}}\phi (x^*)},\, {{{\,\mathrm{Exp}\,}}_{x^*}^{-1}(y)} \right\rangle _{x^*} \ge 0\) for all \(y\in \mathcal {X}\).
2.2 Projection-free vs. Projection-based methods
The growing body of literature on Riemannian optimization considers mostly projection-based methods, such as Riemannian Gradient Decent (RGD) or Riemannian Steepest Decent (RSD) [1]. Such methods and their convergence guarantees typically require Lipschitz assumptions. However, the objectives of many classic optimization and machine learning tasks are not Lipschitz on the whole manifold. In such cases, an additional compactness argument is required. However, in projection-based methods, the typically used retraction back onto the manifold may not be guaranteed to land in this compact set. Thus, in each iteration, an additional and potentially expensive projection step is needed to ensure that the update remains in the compact region where the gradient is Lipschitz. On the other hand, projection-free methods, such as FW, bypass this issue, because their update is guaranteed to stay within the compact feasible region. Importantly, in some problems, the Riemannian linear oracle at the heart of FW can be less expensive than computing a projection back onto the compact set. A detailed numerical study comparing the complexity of projections with that of computing linear minimizers in the Euclidean case can be found in [18]. The efficiency of linear minimizers is especially significant for the applications highlighted in this paper, where the linear oracle even admits a closed form solution (see Sect. 4.1).
2.3 Constrained optimization in Riemannian space
A large body of literature has considered the problem of translating a constrained Euclidean optimization problem into an unconstrained Riemannian problem, by encoding the primary constraint in the manifold structure. However, often a problem has additional constraints, requiring a Riemannian approach to constrained optimization. We list below notable examples, including those that will be covered in the application section of the paper.
Examples on the manifold of positive definite matrices include the computation of Riemannian centroids (with interval constraints, see Sect. 4.2.1) and learning determinantal point processes (with interval constraints [44]). A related problem is that of computing Wasserstein-Barycenters on the Bures manifold (wirh interval constraints, see Sect. 4.3.1). The k-means clustering algorithm corresponds to an optimization task on the Stiefel manifold with equality and inequality constraints [14]. Non-negative PCA can be computed on the sphere with equality constraints [47]. The synchronization of data matrices can be written as an optimization task on the manifold of the orthogonal group with a determinant constraint (see [61, Sect. 5]). Computing a minimum balanced cut for graph bisection can be computed on the Oblique manifold with quadratic equality constraints [41].
3 Riemannian Frank-wolfe
The condition \(\left\langle {{{\,\mathrm{grad}\,}}\phi (x^*)},\, {{{\,\mathrm{Exp}\,}}_{x^*}^{-1}(y)} \right\rangle _{x^*} \ge 0\) for all \(y\in \mathcal {X}\) in Proposition 1 lies at the heart of Frank-Wolfe (also known as “conditional gradient”) methods. In particular, if this condition is not satisfied, then there must be a feasible descent direction — FW schemes seek such a direction and update their iterates [20, 29]. This high-level idea is equally valid in the Riemannian setting. Algorithm 1 recalls the basic (Euclidean) FW method, which solves \(\min _{x\in \mathcal {X}}\phi (x)\), and Algorithm 2 introduces its Riemannian version (RFW), obtained by simply replacing Euclidean objects with their Riemannian counterparts. In the following, \(\left\langle {\cdot },\, {\cdot } \right\rangle \) will denote \(\left\langle {\cdot },\, {\cdot } \right\rangle _{x_k}\) unless otherwise specified.

Notice that to implement Algorithm 1, \(\mathcal {X}\) must be compact and convex. Convexity ensures that after the update in Step 5, \(x_{k+1}\) remains feasible, while compactness ensures that the linear oracle in Step 3 has a solution. To obtain RFW, we first replace the linear oracle (Step 3 in Algorithm 1) with the Riemannian “linear oracle”:
where now \(\mathcal {X}\) is assumed to be a compact g-convex set. Similarly, observe that Step 5 of Algorithm 1 updates the current iterate \(x_k\) along a straight line joining \(x_k\) with \(z_k\). Thus, by analogy, we replace this step by moving \(x_k\) along a geodesic joining \(x_k\) with \(z_k\). The resulting RFW algorithm is presented as Alg 2.

While we obtained Algorithm 2 purely by analogy, we must still show that this analogy results in a valid algorithm. In particular, we need to show that Algorithm 2 converges to a solution of (1). We will in fact prove a stronger result that RFW converges globally at the rate O(1/k), i.e., \(\phi (x_k)-\phi (x^*) = O(1/k)\), which matches the rate of the Euclidean FW method.
3.1 Convergence analysis
We make the following smoothness assumption:
Assumption 1
(Smoothness) The objective \(\phi \) has a locally Lipschitz continuous gradient on \(\mathcal {X}\), that is, there exists a constant L such that for all \(x, y \in \mathcal {X}\) we have
Next, we introduce a quantity that will play a central role in the convergence rate of RFW, namely the curvature constant
An analogous quantity is used in the analysis of the Euclidean FW [29]. In the following we adapt proof techniques from [29] to the Riemannian setting. Here and in the following, \(y=\gamma (\eta )\) for some \(\eta \in [0,1]\) and a geodesic map \(\gamma :[0,1] \rightarrow \mathcal {M}\) with \(\gamma (0) = x\) and \(\gamma (1) = z\) (denoted in the following as \(\gamma _{xz}\)). Lemma 1 relates the curvature constant (11) to the Lipschitz constant L.
Lemma 1
Let \(\phi : \mathcal {M}\rightarrow \mathbb {R}\) be L-smooth on \(\mathcal {X}\), and let \(\mathrm {diam}(\mathcal {X}) := \sup _{x,y \in \mathcal {X}}d{(x,y)}\). Then, the curvature constant \(M_\phi \) satisfies the bound \(M_{\phi } \le L \; \mathrm{diam}(\mathcal {X})^2\).
Proof
Let \(x, z \in \mathcal {X}\) and \(\eta \in (0,1)\); let \(y=\gamma _{xz}(\eta )\) be a point on the geodesic joining x with z. This implies \(\frac{1}{\eta ^2} d{(x,y)}^2 = d{(x,z)}^2\). From (6) we know that
whereupon using the definition of the curvature constant we obtain
\(\square \)
We note below an analog of the Lipschitz inequality (6) using the constant \(M_\phi \).
Lemma 2
(Lipschitz) Let \(x, y, z \in \mathcal {X}\) and \(\eta \in [0,1]\) with \(y=\gamma _{xz}(\eta )\). Then,
Proof
From definition (11) of the constant \(M_\phi \) we see that
which we can rewrite as
Furthermore, since \(y=\gamma _{xz}(\eta )\), we have \({{\,\mathrm{Exp}\,}}_x^{-1} (y) = \eta {{\,\mathrm{Exp}\,}}_x^{-1} (z)\), and therefore
Plugging this equation into (13) the claim follows. \(\square \)
We need one more technical lemma (easily verified by a quick induction).
Lemma 3
(Stepsize for RFW) Let \((a_k)_{k \in I}\) be a nonnegative sequence that fulfills
If \(s_k = \frac{2}{(k+2)}\), then, \(a_k \le \frac{2M_{\phi }}{(k+2)}\).
We are now ready to state our first main convergence result, Theorem 1 that establishes a global iteration complexity for RFW.
Theorem 1
(Rate) Let \(s_k = \frac{2}{k+2}\), and let \(X^*\) be a minimum of \(\phi \). Then, the sequence of iterates \(X_k\) generated by Algorithm 2 satisfies \(\phi (X_k)-\phi (X^*) = O(1/k)\).
Proof
The proof of this claim is straightforward; indeed
where the first inequality follows from Lemma 2, while the second one from \(Z_k\) being an \({{\,\mathrm{argmin}\,}}\) obtained in Step 3 of the algorithm. The third inequality follows from g-convexity of \(\phi \). Setting \(a_k=\phi (X_k)-\phi (X^*)\) in Lemma 3 we immediately obtain
which is the desired O(1/k) convergence rate. \(\square \)
Theorem 1 provides a global sublinear convergence rate for RFW. Typically, FW methods trade off their simplicity for this slower convergence rate, and even for smooth strongly convex objectives they do not attain linear convergence rates [29]. We study in Sect. 3.2 a setting that permits RFW to attain a linear rate of convergence.
3.2 Linear convergence of RFW
In general, the sublinear convergence rate that we derived in the previous section is best-possible for Frank-Wolfe methods. This is due to the following phenomenon, which has been studied extensively in the Euclidean setting [13, 62]: If the optimum lies on the boundary of the constraint set \(\mathcal {X}\), then the FW updates “zig-zag”, resulting in a slower convergence. In this case, the upper bound on the global convergence rate is tight. If, however, the optimum lies in the strict interior of the constraint set, Euclidean FW is known to converge at a linear rate [22, 23]. Remarkably, under a similar assumption, RFW also displays global linear convergence, which we will formally prove below (Theorem 2). Notably, for the special case of the geometric matrix mean that we analyze in the next section, this strict interiority assumption will always be valid, provided that not all the matrices are the same.
3.2.1 Linear convergence under strict interior assumption
We use a Riemannian extension to the well-known Polyak-Łojasiewicz (PL) inequality [42, 49], which we define below. Consider the minimization
and let \(f^{*}\) be the optimal function value. We say that f satisfies the PL inequality if for some \(\mu > 0\),
Inequality (15) is weaker than strong convexity (and is in fact implied by it). It has been widely used for establishing linear convergence rates of gradient-based methods; see [33] for several (Euclidean) examples, and [65] for a Riemannian example. We will make use of inequality (15) for obtaining linear convergence of RFW, by combining it with a strict interiority condition on the minimum.
Theorem 2
(Linear convergence RFW) Suppose that \(\phi \) is strongly g-convex with constant \(\mu \) and that its minimum lies in a ball of radius r that strictly inside the constraint set \(\mathcal {X}\). Define \(\varDelta _k := \phi (X_k)-\phi (X^*)\) and let the step-size \(s_k = \frac{r\sqrt{\mu \varDelta _k}}{\sqrt{2}M_\phi }\). Then, RFW converges linearly since it satisfies
Proof
Let \(\mathcal {B}_r(X^*) \subset \mathcal {X}\) be a ball of radius r containing the optimum. Let
be the direction of steepest descent in the tangent space \(\mathcal {T}_{X_k}\). The point \(P_k = {{\,\mathrm{Exp}\,}}_{X_k}(rW_k)\) lies in \(\mathcal {X}\). Consider now the following inequality
which follows upon using the definition of \(W_k\). Thus, we have the bound
where the first inequality follows from the Lipschitz-bound (Lemma 2), the second one from (16), and the third one from the PL inequality (which, in turn holds due to the \(\mu \)-strong g-convexity of \(\phi \)). Now setting the step size \(s_k = \frac{r\sqrt{\mu \varDelta _k}}{\sqrt{2}M_\phi }\), we obtain
which delivers the claimed linear convergence rate. \(\square \)
Theorem 2 provides a setting where RFW can converge fast, however, it uses step sizes \(s_k\) that require knowing \(\phi (X^*)\)Footnote 1; in case the optimal value is not available, we can use a worse value, which will still yield the desired inequality.
Remark 1
(Necessity of strict interior assumption) For optimization tasks with polytope constraints that do not fulfill a strict interior assumption as the one described above, several EFW variants achieve linear convergence [36]. Notable examples include Away-step FW [23, 62], Pairwise FW [45] and Fully-corrective FW [26]. One may ask, whether these variants can be generalized to the Riemannian case. The first difficulty lies in finding a Riemannian equivalent of the polytope constraint set, which is defined as the convex hull of a finite set of vectors (atoms). Naturally, we could consider the convex hull of a finite set of points on a manifold, which is the intersection of all convex set that contain them. Unfortunately, such a set is in general not compact – compactness is only guaranteed for Hadamard manifolds under additional, restrictive conditions [39]. Even in this special case, ensuring that the resulting constraint sets have sufficiently “good” geometry is not straightforward.
3.3 RFW for nonconvex problems
Finally, we want to consider the case where \(\phi \) in Eq. 1 may be nonconvex. In this case, we cannot hope to find the global minimum with first-order methods, such as RFW. However, we can compute first-order critical point via RFW. For the setup and analysis, we follow the Euclidean case [35].
We first introduce the Frank-Wolfe gap as a criterion for evaluating convergence rates. For \(X \in \mathcal {X}\), we write
With this, we can show the following sublinear convergence guarantee:
Theorem 3
(Rate (nonconvex case)) Let \({\tilde{G}}_k := \min _{0 \le k \le K} G(X_k)\) (where \(G(X_k)\) denotes the Frank-Wolfe gap at \(X_k\)). After K iterations of Algorithm 2, we have \({\tilde{G}}_k \le \frac{\max \lbrace 2 h_0, M_{\phi } \rbrace }{\sqrt{K+1}}\).
The proof utilizes techniques similar to those in [35, Theorem 1].
4 Specializing RFW for HPD matrices
In this section we study a concrete setting for RFW, namely, a class of g-convex optimization problems with Hermitian positive definite (HPD) matrices. We will show that the Riemannian linear oracle (9) admits an efficient solution for this class of problems, thereby allowing an efficient implementation of Algorithm 2. The concrete class of problems that we consider is the following:
where \(\phi \) is a g-convex function and \(\mathcal {X}\) is a “positive definite interval” (which is easily seen to be a g-convex set). Note that the set \(\mathcal {X}\) actually does not admit an easy projection for matrices. Problem (18) captures several g-convex optimization problems, of which perhaps the best known is the task of computing the matrix geometric mean (also known as the the Riemannian centroid or Karcher mean)—see Sect. 4.2.1.
We briefly recall some facts about the Riemannian geometry of HPD matrices below. For a comprehensive overview, see, e.g., [5, Chapter 6]. We denote by \(\mathbb {H}_d\) the set of \(d\times d\) Hermitian matrices. The most common Riemannian geometry on \(\mathbb {P}_d\) is induced by
This metric induces the geodesic \(\gamma : [0,1]\rightarrow \mathbb {P}_d\) between \(X, Y \in \mathbb {P}_d\) given by
The corresponding Riemannian distance is
The Riemannian gradient \({{\,\mathrm{grad}\,}}\phi \) is obtained from the Euclidean one (\(\nabla \phi \)) as follows
where \(\nabla ^\mathbb {H}\phi (X) := \frac{1}{2} \big ( \nabla \phi (X) + (\nabla \phi (X))^* \big )\) denotes the (Hermitian) symmetrization of the gradient. The exponential map and its inverse at a point \(P \in Pd\) are given by
where \(\exp (\cdot )\) and \(\log (\cdot )\) denote the matrix exponential and logarithm, respectively. Observe that using (22) we obtain the identity
With these details, Algorithm 2 can almost be applied to (18) — the most crucial remaining component is the Riemannian linear oracle, which we now describe.
4.1 Solving the Riemannian linear oracle
For solving (18), the Riemannian linear oracle (see (9)) requires solving
Problem (24) is a non-convex optimization problem over HPD matrices. However, remarkably, it turns out to have a closed form solution. Theorem 4 presents this solution and is our main technical result for Sect. 4.
Theorem 4
Let \(L, U \in \mathbb {P}_d\) such that \(L \prec U\). Let \(S \in \mathbb {H}_d\) and \(X \in \mathbb {P}_d\) be arbitrary. Then, the solution to the optimization problem
is given by \(Z = X^{-1}Q \left( P^* [-{{\,\mathrm{sgn}\,}}(D)]_+ P + {\hat{L}}\right) Q^*X^{-1}\), where \(S=QDQ^*\) is a diagonalization of S, \({\hat{U}} - {\hat{L}}=P^* P\) with \({\hat{L}}=Q^* X L X Q\) and \({\hat{U}}=Q^* X U X Q\).
For the proof of Theorem 4, we need a fundamental lemma about eigenvalues of Hermitian matrices (Lemmas 4). First, we need to introduce some additional notation. For \(x \in {\mathbb {R}}^d\), let \(x^\downarrow = \left( x_1^\downarrow , \dots , x_d^\downarrow \right) \) denote the vector with entries of x in decreasing order, i.e., \(x_1^\downarrow \ge \ldots \ge x_d^\downarrow \). For \(x, y \in {\mathbb {R}}^d\) we say that x is weakly majorized by y (\(x \prec _w y\)), if \(\sum _{i=1}^k x_i^\downarrow \le \sum _{i=1}^k y_i^\downarrow \) for \(1 \le k \le d\). We can now recall the following lemma on eigenvalues of Hermitian matrices, which can be found, e.g., in [4, Problem III.6.14]:
Lemma 4
([4]) Let X, Y be HPD matrices. Then
where \(\lambda ^\downarrow (X)\) (\(\lambda ^\uparrow \)) denote eigenvalues of X arranged in decreasing (increasing) order, \(\prec _w\) denotes the weak majorization order and \(\cdot \) denotes the elementwise product. If X, Y are Hermitian, we have
with equality, if the the product XY is symmetric.
Remark 2
We recall a well-known fact on solving the trace minimization problem \(\min _{Y} {{\,\mathrm{tr}\,}}{XY}\). Diagonalizing X, Y allows for rewriting the minimization problem as \(\min _S {{\,\mathrm{tr}\,}}{DQ^T S Q}\), where D, S are diagonal and Q orthogonal. To see for which S the minimum is attained, note that \(\min \sum _{ij}d_i s_j q_{ij}^2 \ge \min \sum _{ij} d_i s_j r_{ij}\), where \((r_{ij})\) is doubly-stochastic. By Birkhoff’s theorem the minimum occurs for permutation matrices, i.e., \(\min \sum _{i} d_i s_{\sigma (i)}\). By the rearrangement inequality this is minimized, if the order of the indices is reversed.
Proof
(Theorem 4) First, introduce the variable \(Y=XZX\); then (25) becomes
where the constraints have also been modified to \(L' \preceq Y \preceq U'\), where \(L'=XLX\) and \(U'=XUX\). Diagonalizing S as \(S=QDQ^*\), we see that \({{\,\mathrm{tr}\,}}(S\log Y) = {{\,\mathrm{tr}\,}}(D\log W)\), where \(W=Q^*YQ\). Thus, instead of (26) it suffices to solve
where \(L''=Q^*L'Q\) and \(U''=Q^*U'Q\). We have strict inequality \(U'' \succ L''\), thus, our constraints are \(0 \prec W-L'' \preceq U''-L''\), which we may rewrite as \(0 \prec R \preceq I\), where \(R = (U''-L'')^{-\nicefrac {1}{2}}(W-L'')(U''-L'')^{-\nicefrac {1}{2}}\). Notice that
Thus, problem (27) now turns into
where \(U'' - L''=P^* P\). We want to construct an R that attains the minimum. Note that using Lemma 4 we see that
Remark 2 ensures that the minimum attains the lower bound, i.e., the minimum is attained by matching the eigenvalues of D and \(\log (P^*R P+L'')\) in reverse orders. Note that the matrix logarithm \(\log (\cdot )\) and the map \(R \mapsto P^* R P +L''\) are operator monotone. Now, without loss of generality, assume that R is diagonal and recall that, by construction \(0 \prec R \preceq I\). Consider
This ensures that
-
1.
if \(d_{ii}>0\), the corresponding element of \(\lambda ^\downarrow (\log (P^* R P +L''))\) is minimized,
-
2.
if \(d_{ii} \le 0\), the corresponding element of \(\lambda ^\downarrow (\log (P^* R P+L''))\) is maximized.
With that, the minimum of the trace is attained. Thus, we see that
and we immediately obtain the optimal \(Z=X^{-1}YX^{-1}\). \(\square \)
Remark 3
Computing the optimal direction \(Z_k\) takes one Cholesky factorization, two matrix square roots (Schur method), eight matrix multiplications, and one eigenvalue decomposition. This gives a complexity of \(O(N^3)\). On our machines, we report \(\approx \frac{1}{3} N^3 + 2 \times 28.{\bar{3}} N^3 + 8 \times 2N^3 + 20 N^3 \approx 93 N^3\).
4.2 Application to the Riemannian mean
4.2.1 Computing the Riemannian mean
Statistical inference frequently involves computing averages of input quantities. Typically encountered data lies in Euclidean spaces where arithmetic means are the “natural” notions of averaging. However, the Euclidean setting is not always the most natural or efficient way to represent data. Many applications involve non-Euclidean data such as graphs, strings, or matrices [38, 48]. In such applications, it is often beneficial to represent the data in its natural space and adapt classical tools to the specific setting. In other cases, a problem might be very hard to solve in Euclidean space but may become more accessible when viewed through a different geometric lens. Specifically, with a suitable choice of the Riemannian metric, a Euclidean nonconvex problem may be geodesically convex. Hence, we can give global convergence guarantees for solving such problems with Riemannian optimization methods.
This section considers one of these cases, namely the problem of determining the geometric matrix mean (Karcher mean problem). While there exists an intuitive notion for the geometric mean of sets of positive real numbers, this notion does not immediately generalize to sets of positive definite matrices due to the lack of commutativity on matrix spaces. Over a collection of Hermitian, positive definite matrices the geometric mean can be viewed as the geometric optimization problem
where \(\delta _R\) denotes the Riemannian metric. In a Euclidean setting, the problem is non-convex. However, one can view Hermitian, positive matrices as points on a Riemannian manifold and compute the geometric mean as the Riemannian centroid. The corresponding optimization problem (Eq. 30) is geodesically convex [51]. In this section, we look at the problem through both geometric lenses and provide efficient algorithmic solutions while illustrating the benefits of switching geometric lenses in geometric optimization problems.
There exists a large body of work on the problem of computing the geometric matrix means [30]. Classic algorithms like Newton’s method or Gradient Decent (GD) have been successfully applied to the problem. Standard toolboxes implement efficient variations of GD like Steppest Decent or Conjugate Gradient (Manopt [11]) or Richardson-like linear-gradient decent (Matrix Means Toolbox [9]). Recent work by Yuan et al. [64] analyzes condition numbers of Hessians in Riemannian and Euclidean steepest-decent approaches that provide theoretical arguments for the good performance of Riemannian approaches.
Recently, T. Zhang developed a majorization-minimization approach with asymptotic linear convergence [67]. In this section, we use the Riemannian Frank-Wolfe algorithm for computing the geometric matrix mean. Here, we exploit the strong geodesic convexity of the problem to achieve global linear convergence. To complement this analysis, we show that recent advances in nonconvex analysis [35] can be used to develop a Frank-Wolfe scheme (EFW) for the nonconvex Euclidean case (see Appendix 1).
In the simple case of two PSD matrices, X and Y, one can view the geometric mean as their metric midpoint computed by [34]
More generally, for a collection of M matrices, the geometric mean can be seen as a minimization problem of the sum of squares of distances [6],
where \(\delta _R(X,Y)=\Vert {\log (X^{-\frac{1}{2}} Y X^{-\frac{1}{2}})}\Vert _F\) as introduced earlier. Here we consider the more general weighted geometric mean:
E. Cartan showed in a Riemannian setting that a global minimum exists, which led to the term Cartan mean frequently used in the literature. In this setting, one can view the collection of matrices as points on a Riemannian manifold. H. Karcher associated the minimization problem with that of finding centers of masses on these manifolds [32], hence motivating a second term to describe the geometric matrix mean (Karcher mean).
The geometric matrix mean enjoys several key properties. We list below the ones of crucial importance to our paper and refer the reader to [37, 40] for a more extensive list. To state these results, we recall the general form of the two other basic means of operators: the (weighted) harmonic and arithmetic means, denoted by H and A respectively.
Then, one can show the following well-known operator inequality that relates H, G, and A:
Lemma 5
(Means Inequality, [5]) Let \(A_1,\ldots ,A_M > 0\), and let H, G, and A denote their (weighted) harmonic, geometric, and arithmetic means, respectively. Then,
The key computational burden of all our algorithms lies in computing the gradient of the objective function (30). A short calculation (see e.g., [5, Ch. 6]) shows that if \(f(X) = \delta _R^2(X,A)\), then \(\nabla f(X) = X^{-1}\log (XA^{-1})\). Thus, we immediately obtain
4.2.2 Implementation
We compute the geometric matrix mean with Algorithm 2. For the PSD manifold, line 3 can be written as
Note that the operator inequality \(H \preceq G \preceq A\) given by Lemma 5 plays a crucial role: It shows that the optimal solution lies in a compact set so we may as well impose this compact set as a constraint to the optimization problem (i.e., we set \(\mathcal {X}=\lbrace H \preceq Z \preceq A \rbrace \)). We implement the linear oracles as discussed above: In the Euclidean case, a closed-form solution is given by
where \(A-H = P^*P\) and \(P\nabla \phi (X_k)P^* = Q\varLambda Q^*\) (see Thm. 7). Analogously, for the Riemannian case, the “linear” oracle
is well defined and solved by
with \({\hat{A}}-{\hat{H}}=P^{*}P\), \({\hat{A}}=Q^* A Q\), \({\hat{H}}=Q^{*}HQ\) and \(\nabla \phi (X_k) = Q\varLambda Q^*\) (see Thm. 4). The resulting Frank-Wolfe method for the geometric matrix mean is given by Algorithm 3.

4.3 Application to Bures-wasserstein barycenters
4.3.1 Computing Bures-Wasserstein barycenters on the Gaussian density manifold
As a second application of RFW, we consider the computation of Bures-Wasserstein barycenters of multivariate (centered) Gaussians. This application is motivated by optimal transport theory; in particular, the Bures-Wasserstein barycenter is the solution to the multi-marginal transport problem [8, 43]: Let \(\lbrace A_i \rbrace _{i=1}^m \in {\mathbb {P}}_d\) and \(w=(w_1,\ldots , w_m)\) a vector of weights (\(\sum _i w_i =1; \; w_i >0, \forall i\)). The minimization task
is called multi-marginal transport problem. Its unique minimizer
is the Bures-Wasserstein barycenter. Here, \(d_W\) denotes the Wasserstein distance
To see the connection to optimal transport, note that Eq. 39 corresponds to a least-squares optimization over a set of multivariate center Gaussians with respect to the Wasserstein distance. The Gaussian density manifold is isomorphic to the manifold of symmetric positive definite matrices, which allows for a direct application of RFW and the setup in the previous section to Eq. 39, albeit with a different set of constraints. In the following, we discuss a suitable set of constraints and adapt RFW for the computation of the Bures-Wasserstein barycenter (short: Wasserstein mean).
First, note that as for the Karcher mean, one can show that the Wasserstein mean of two matrices is given in closed form; namely as
However, the computation of the barycenter of m matrices (\(m>2\)) requires solving a quadratic optimization problem. Note, that Eq. 41 defines a geodesic map from X to Y. Unfortunately, an analog of the means inequality does not hold in the Wasserstein case. However, one can show, that the arithmetic matrix mean always gives an upper bound, providing one-sided constraints [7]:
and similarly for the arithmetic mean \(A(w; \lbrace A_i \rbrace )\) of m matrices. Moreover, one can show that \(\alpha I \preceq X\) [8], where \(\alpha \) is the minimal eigenvalue over \(\lbrace A_i \rbrace _{i=1}^m\), i.e.
In summary, this gives the following constraints on the Wasserstein mean:
Next, we will derive the gradient of the objective function. According to Eq. 39, the objective is given as
Two expressions for the gradient of (43) are derived in the following.
Lemma 6
Let \(\phi \) be given by (43). Then, its gradient is
Proof
Note that \(\frac{d}{dX} {{\,\mathrm{tr}\,}}(X) = I\). Consider
where (1) follows from the chain rule and (2) from A and X being symmetric and positive definite: If A and X are symmetric and positive definite, then A has a unique positive definite root \(A^{1/2}\) and therefore
Putting everything together, the desired expression follows as
\(\square \)
4.3.2 Implementation
Given a set of constraints and an expression for the gradient, we can solve Eq. 39 with RFW using the following setup: We write the log-linear oracle as
where \({{\,\mathrm{grad}\,}}\phi (X)\) is the Riemannian gradient of \(\phi \) and \({{\,\mathrm{Exp}\,}}_X^{-1}(Z) \) the exponential map with respect to the Riemannian metric. The constraints are given by Eq. 42. Since the constraint set is given by an interval of the form \(L \preceq Z \preceq U\), the oracle can be solved in closed form using Theorem 4. The resulting algorithm is given in Algorithm 3.
5 Approximately solving the Riemannian “linear” oracle
In the previous section, we have given examples of applications where the Riemannian “linear” oracle can be solved in closed form – rendering the resulting RFW algorithm into a practical method. Unfortunately, the “linear” oracle is in general a nonconvex subroutine. Therefore, it can be challenging to find efficient solutions for constrained problems in practice.
One remedy for such situations is to solve the “linear” oracle only approximately. In the following, we show that we can recover sublinear convergence rates for RFW, even if we solve the “linear” oracle only approximately. This extension greatly widens the range of possible applications for RFW. For instance, while we currently do not have closed-form solutions for the“linear” oracle in some of the examples in Sect. 2.3, we could find approximate solutions via relaxations or iteratively solving the respective subroutine.
In the following, we say that \(Z' \in \mathcal {X}\) is a \(\delta \)-approximate linear minimizer, if
We give the following sublinear convergence guarantee:
Theorem 5
Let \(X^*\) be a minimum of a geodesically convex function \(\phi \) and \(\delta \ge 0\) the accuracy to which the “linear” oracle is solved in each round. Then, the sequence of iterates \(X_k\) generated by Algorithm 2 satisfies
The proof relies on adapting proof techniques from [17, 29] to the Riemannian setting. It utilizes the following auxiliary lemma:
Lemma 7
For a steps size \(\eta \in (0,1)\) and accuracy \(\delta \), we have
A proof of the Lemma can be found in Appendix 1. The proof of Theorem 5 follows then from Lemma 3 and 8 similar to Theorem 1.
6 Computational experiments
In this section, we will remark on the implementation of Algorithm 3 and show numerical results for computing Riemannian centroids for different parameter choices. To evaluate the efficiency of our method, we compare the performance of RFW against that of a selection of state-of-the-art methods. Additionally, we use Algorithm 3 to compute Wasserstein barycenters of positive definite matrices. All computational experiments are performed using Matlab.
6.1 Computational considerations
When implementing the algorithm we can take advantage of the positive definiteness of the input matrices. For example, if using Matlab, rather than computing \(X^{-1}\log (XA_i^{-1})\), it is more preferable to compute
because both \(X^{-\nicefrac {1}{2}}\) and \(\log (X^{\nicefrac {1}{2}}A_i^{-1}X^{\nicefrac {1}{2}})\) can be computed by suitable eigendecomposition. In contrast, computing \(\log (XA_i^{-1})\) invokes the matrix logarithm (logm in Matlab), which can be much slower.
To save on computation time, we prefer to use a diminishing scalar as the stepsize in Algorithm 3. In principle, this simple stepsize selection could be replaced by a more sophisticated Armijo-like line-search or even exact minimization by solving
This stepsize tuning may accelerate the convergence speed of the algorithm, but it must be combined with a more computational intensive strategy of “away” steps [23] to obtain a geometric rate of convergence. However, we prefer Algorithm 3 for its simplicity and efficiency.
Theorems 1 and 3 show that Algorithm 2 converges at the global (non-asymptotic) rates \(O(1/\epsilon )\) (g-convex RFW) and \(O(1/\epsilon ^2)\) (nonconvex RFW). However, by further exploiting the simple structure of the constraint set and the “curvature” of the objective function, we might obtain a stronger convergence result.
6.2 Numerical results
We present numerical results for computing the Riemannian and Wasserstein means for sets of positive definite matrices. We test our methods on both well- and ill-conditioned matrices; the generation of sample matrices is described in the appendix. An extended arXiv version of the paper [61] contains additional examples and numerical experiments.
6.2.1 Computing the Riemannian Mean
To test the efficiency of our method, we implement RFW (Algorithm 3) in Matlab and compare its performance on the problem of computing the Riemannian mean against related state-of-the-art Riemannian optimization methods:
-
1.
Riemannian L-BFGS (R-LBFGSFootnote 2) is a quasi-Newton method that iteratively approximates the Hessian for evaluating second-order information [63].
-
2.
Riemannian Barzilai–Borwein (BB) is a first-order gradient-based method for constrained and unconstrained optimization. It evaluates second-order information from an approximated Hessian to choose the stepsize [28]. We use the Manopt version of RBB.
-
3.
Matrix Means Toolbox (MM) [9] is an efficient Matlab toolbox for matrix optimization. Its implementation of the geometric mean problem uses a Richardson-like iteration of the form
$$\begin{aligned} X_{k+1} \leftarrow X_k - \alpha X_k \sum _{i=1}^n \log (A_i^{-1} X_k) \; , \end{aligned}$$with a suitable \(\alpha >0\).
-
4.
Zhang [67] is a recently published majorization-minimization method for computing the geometric matrix mean.
Note that this selection reflects a broad spectrum of commonly used methods for Riemannian optimization. It ranges from highly specialized approaches that are targeted to the Karcher mean (MM), to more general and versatile methods (e.g., R-LBFGS). A careful evaluation should take both computing time and algorithmic features, such as the number of calls to oracles and loss functions, into account. We perform and further discuss such an evaluation below. For completeness, we also compare against RFW ’s Euclidean counterpart EFW (Algorithm 4).
We generate a set A of m positive definite matrices of size n and compute the geometric mean with EFW and RFW as specified in Algorithms 3 and 4. To evaluate the performance of the algorithm, we compute the cost function
after each iteration. We further include an experiment, where we report the gradient norm \(\Vert {{{\,\mathrm{grad}\,}}f}\Vert _F\).
Figure 1 shows performance comparisons of all methods for different parameter choices and condition numbers. In a second experiment (Fig. 2) we compare inputs with different condition numbers for two initialization, the harmonic mean and a matrix \(A_i \in A\). We observe that RFW outperforms BB for all inputs and initializations. Furthermore, RFW performs competitively in comparison with R-LBFGS, Zhang’s Method and MM. The competetive performance of RFW is consistent across different initializations. In a third experiment we compared the accuracy reached by RFW with R-LBFGS as the (in our experiments) most accurate Riemannian state-of-the-art method (Fig. 3). We observe that RFW reaches a medium accuracy fast; however, ultimately R-LBFGS reaches a higher accuracy.
In comparison with EFW, we observe that RFW reaches a similar performance and accuracy. The numerical advantage of EFW may be due to implementation differences between Riemannian and Euclidean methods.
In addition, we include a comparison of the number of internal calls to cost and gradient functions (Fig. 1) for all methods. Note that this comparison evaluates algorithmic features and is therefore machine-independent. The reported numbers were obtained by averaging counts over ten experiments with identical parameter choices. We observe that RFW (and EFW) avoid internal calls to the gradient and cost function, requiring only a single gradient evaluation per iteration. This results in the acceleration (i.e., faster convergence) observed in the plots.
6.2.2 Computing Wasserstein barycenters
Performance of RFW for computing the Wasserstein mean for m well- (left) and M ill-conditioned matrices (right) of size n for MaxIt iteration and three initializations: (1) \(X_0\) is set to one of the matrices in the set A, i.e., \(A_i \in A\); (2) \(X_0\) is initialized as the arithmetic mean of A, i.e., the upper bound of the constraint set; and (3) \(X_0\) is set to the lower bound \(\alpha I\) of the constraint, where \(\alpha \) is the minimal eigenvalue over A
To demonstrate the versatility of our approach, we use RFW to compute Bures-Wasserstein barycenters. For this, we adapt the above-described setup to implement Algorithm 3. Fig. 4 shows the performance of RFW on both well- and ill-conditioned matrices. We compare three different initializations in each experiment: In (1), we choose an arbitrary element of A as starting point (\(X_0 \sim {\mathcal {U}}(A)\)). The other experiments start at the lower and upper bounds of the constraint set, i.e., (2) \(X_0\) is set to the arithmetic mean of A and (3) \(X_0=\alpha I\), where \(\alpha \) is the smallest eigenvalue over A. Our results suggest that RFW performs well when initialized from any point in the feasible region, even on sets of ill-conditioned matrices.
7 Discussion
We presented a Riemannian version of the classical Frank-Wolfe method that enables constrained optimization on Riemannian (more precisely, on Hadamard) manifolds. Similar to the Euclidean case, we recover sublinear convergence rates for Riemannian Frank-Wolfe for both geodesically convex and nonconvex objectives. Under the stricter assumption of \(\mu \)-strongly g-convex objectives and a strict interiority condition on the constraint set, we show that even linear convergence rates can be attained by Riemannian Frank-Wolfe. To our knowledge, this work represents the first extension of Frank-Wolfe methods to a manifold setting.
In addition to the general results, we present an efficient algorithm for optimization on Hermitian positive definite matrices. A key highlight of this specialization is a closed-form solution to the Riemannian “linear” oracle needed by Frank-Wolfe (this oracle involves solving a nonconvex problem). While we focus on the specific problem of computing the Karcher mean (also known as the Riemannian centroid or geometric matrix mean), the derived closed-form solutions apply to more general objective functions and should be of wider interest for related nonconvex and g-convex problems. To demonstrate this versatility, we also included an application of RFW to the computation of Wasserstein barycenters on the Gaussian density manifold. In future work, we hope to explore other constraint sets and matrix manifolds that admit an efficient solution to the Riemannian “linear” oracle.
Our algorithm is shown to be competitive against a variety of established and recently proposed approaches [28, 63, 67] providing evidence for its applicability to large-scale statistics and machine learning problems. In follow-up work [60], we show that RFW extends to nonconvex stochastic settings, further increasing the efficiency and versatility of Riemannian Frank-Wolfe methods. Exploring the use of this class of algorithms in large-scale machine learning applications is a promising avenue for future research.
Notes
This step size choice is reminiscent of the so-called “Polyak stepsizes” used in the convergence analysis of subgradient methods [50].
Also known as LRBFGS.
References
Absil, P.A., Mahony, R., Sepulchre, R.: Optimization algorithms on matrix manifolds. Princeton University Press Princeton, NJ (2009)
Bach, F.: Duality between subgradient and conditional gradient methods. SIAM J. Optim. 25(1), 115–129 (2015)
Bento, G.C., Ferreira, O.P., Melo, J.G.: Iteration-complexity of gradient, subgradient and proximal point methods on Riemannian manifolds. J. Optim. Theory Appl. 173(2), 548–562 (2017)
Bhatia, R.: Matrix Analysis. Springer, Berlin (1997)
Bhatia, R.: Positive Definite Matrices. Princeton University Press, NJ (2007)
Bhatia, R., Holbrook, J.: Riemannian geometry and matrix geometric means. Linear Algebra Appl. 413, 594–618 (2006)
Bhatia, R., Jain, T., Lim, Y.: On the bures-wasserstein distance between positive definite matrices. Expo. Math. 37(2), 165–191 (2018)
Bhatia, R., Jain, T., Lim, Y.: Strong convexity of sandwiched entropies and related optimization problems. Rev. Math. Phys. 30(09), 1850014 (2018)
Bini, D.A., Iannazzo, B.: Computing the Karcher mean of symmetric positive definite matrices. Linear Algebra Appl. 438(4), 1700–10 (2013)
Boumal, N., Absil, P.A., Cartis, C.: Global rates of convergence for nonconvex optimization on manifolds. arXiv preprint arXiv:1605.08101 (2016)
Boumal, N., Mishra, B., Absil, P.A., Sepulchre, R.: Manopt, a Matlab toolbox for optimization on manifolds. Journal of Machine Learning Research 15, 1455–1459 (2014). http://www.manopt.org
Calinescu, G., Chekuri, C., Pál, M., Vondrák, J.: Maximizing a submodular set function subject to a matroid constraint. SIAM J. Computing 40(6), 1740–1766 (2011)
Canon, M., Cullum, C.: A tight upper bound on the rate of convergence of frank-wolfe algorithm. SIAM J. Control 6, 509–516 (1968)
Carson, T., Mixon, D.G., Villar, S.: Manifold optimization for k-means clustering. In: 2017 International Conference on Sampling Theory and Applications (SampTA), pp. 73–77 (2017). https://doi.org/10.1109/SAMPTA.2017.8024388
Chavel, I.: Riemannian Geometry: A modern introduction, vol. 98. Cambridge University Press, Cambridge (2006)
Cherian, A., Sra, S.: Riemannian dictionary learning and sparse coding for positive definite matrices. arXiv:1507.02772 (2015)
Clarkson, K.L.: Coresets, sparse greedy approximation, and the Frank-Wolfe algorithm. ACM Trans. Algorithms 6(4), 1–30 (2010)
Combettes, C.W., Pokutta, S.: Complexity of linear minimization and projection on some sets. Oper. Res. Lett. 49(4), 565–571 (2021)
Edelman, A., Arias, T.A., Smith, S.T.: The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Analysis Applications (SIMAX) 20(2), 303–353 (1998)
Frank, M., Wolfe, P.: An algorithm for quadratic programming. Naval Research Logistics Quarterly 3(95), 95–110 (1956)
Fujishige, S., Isotani, S.: A submodular function minimization algorithm based on the minimum-norm base. Pacific Journal Optimization 7, 3–17 (2011)
Garber, D., Hazan, E.: Faster rates for the Frank-Wolfe method over strongly-convex sets. In: International Conference on Machine Learning, pp. 541–549 (2015)
GuéLat, J., Marcotte, P.: Some comments on Wolfe’s ‘away step’. Math. Program. 35(1), 110–119 (1986)
Hazan, E., Luo, H.: Variance-reduced and projection-free stochastic optimization. In: International Conference on Machine Learning, pp. 1263–1271 (2016)
Helmke, U., Hüper, K., Lee, P.Y., Moore, J.: Essential matrix estimation using Gauss-Newton iterations on a manifold. Int. J. Comput. Vision 74(2), 117–136 (2007)
Holloway, C.A.: An extension of the frank and wolfe method of feasible directions. Math. Program. 6, 14–27 (1974)
Hosseini, R., Sra, S.: Matrix manifold optimization for Gaussian mixtures. In: NIPS (2015)
Iannazzo, B., Porcelli, M.: The riemannian barzilai-borwein method with nonmonotone line search and the matrix geometric mean computation. IMA J. Numer. Anal. 38(1), 495–517 (2018)
Jaggi, M.: Revisiting Frank-Wolfe: Projection-free sparse convex optimization. In: International Conference on Machine Learning (ICML), pp. 427–435 (2013)
Jeuris, B., Vandebril, R., Vandereycken, B.: A survey and comparison of contemporary algorithms for computing the matrix geometric mean. Electron. Trans. Numer. Anal. 39, 379–402 (2012)
Jost, J.: Riemannian Geometry and Geometric Analysis. Springer, Berlin (2011)
Karcher, H.: Riemannian center of mass and mollifier smoothing. Comm. Pure Appl. Math. 30(5), 509–541 (1977)
Karimi, H., Nutini, J., Schmidt, M.W.: Linear convergence of gradient and proximal-gradient methods under the Polyak-Lojasiewicz condition. CoRR arXiv:1608.04636 (2016)
Kubo, F., Ando, T.: Means of positive linear operators. Math. Ann. 246, 205–224 (1979)
Lacoste-Julien, S.: Convergence rate of Frank-Wolfe for non-convex objectives. arXiv preprint arXiv:1607.00345 (2016)
Lacoste-Julien, S., Jaggi, M.: On the global linear convergence of Frank-Wolfe optimization variants. In: Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1, NIPS’15, pp. 496–504. MIT Press, Cambridge, MA, USA (2015)
Lawson, J., Lim, Y.: Karcher means and Karcher equations of positive definite operators. Trans. Amer. Math. Soc. Ser. B 1, 1–22 (2014)
Le Bihan, D., Mangin, J.F., Poupon, C., Clark, C.A., Pappata, S., Molko, N., Chabriat, H.: Diffusion Tensor Imaging: Concepts and Applications. J. Magn. Reson. Imaging 13(4), 534–546 (2001)
Ledyaev, Y.S., Treiman, J.S., Zhu, Q.J.: Helly’s intersection theorem on manifolds of nonpositive curvature. J. Convex Anal. 13(3/4), 785 (2006)
Lim, Y., Pálfia, M.: Matrix power means and the Karcher mean. J. Funct. Anal. 262(4), 1498–1514 (2012)
Liu, C., Boumal, N.: Simple algorithms for optimization on riemannian manifolds with constraints. Applied Mathematics & Optimization 82(3), 949–981 (2019)
Lojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. Les équations aux dérivées partielles 117, 87–89 (1963)
Malagò, L., Montrucchio, L., Pistone, G.: Wasserstein riemannian geometry of positive-definite matrices ? (2018)
Mariet, Z.E., Sra, S.: Fixed-point algorithms for learning determinantal point processes. In: ICML (2015)
Mitchell, B.F., Dem’yanov, V.F., Malozemov, V.N.: Finding the point of a polyhedron closest to the origin. SIAM J. Control 12(1), 19–26 (1974)
Moakher, M.: Means and averaging in the group of rotations. SIAM J. Matrix Anal. Appl. 24(1), 1–16 (2002)
Montanari, A., Richard, E.: Non-negative principal component analysis: Message passing algorithms and sharp asymptotics. IEEE Trans. Inf. Theory 62(3), 1458–1484 (2016)
Nielsen, F., Bhatia, R. (eds.): Matrix Information Geometry. Springer (2013)
Polyak, B.T.: Gradient methods for minimizing functionals (in Russian). Zh. Vychisl. Mat. Mat. Fiz. 3(4), 643–653 (1963)
Polyak, B.T.: Introduction to Optimization. Optimization Software Inc. (1987). Nov 2010 revision
Pálfia, M.: Operator means of probability measures and generalized karcher equations. Adv. Math. 289, 951–1007 (2016)
Reddi, S.J., Sra, S., Póczos, B., Smola, A.: Stochastic Frank-Wolfe methods for nonconvex optimization. In: Communication, Control, and Computing (Allerton), 2016 54th Annual Allerton Conference on, pp. 1244–1251. IEEE (2016)
Ring, W., Wirth, B.: Optimization methods on Riemannian manifolds and their application to shape space. SIAM J. Optim. 22(2), 596–627 (2012)
Sra, S., Hosseini, R.: Geometric optimisation on positive definite matrices for elliptically contoured distributions. In: Advances in Neural Information Processing Systems, pp. 2562–2570 (2013)
Sra, S., Hosseini, R.: Conic geometric optimization on the manifold of positive definite matrices. SIAM J. Optim. 25(1), 713–739 (2015)
Sun, J., Qu, Q., Wright, J.: Complete Dictionary Recovery over the Sphere II: Recovery by Riemannian Trust-region Method. arXiv:1511.04777 (2015)
Tan, M., Tsang, I.W., Wang, L., Vandereycken, B., Pan, S.J.: Riemannian pursuit for big matrix recovery. In: International Conference on Machine Learning (ICML-14), pp. 1539–1547 (2014)
Udriste, C.: Convex functions and optimization methods on Riemannian manifolds, vol. 297. Springer Science & Business Media, Berlin (1994)
Vandereycken, B.: Low-rank matrix completion by Riemannian optimization. SIAM J. Optim. 23(2), 1214–1236 (2013)
Weber, M., Sra, S.: Projection-free nonconvex stochastic optimization on Riemannian manifolds. IMA J. Numer. Anal. (2021). https://doi.org/10.1093/imanum/drab066
Weber, M., Sra, S.: Riemannian optimization via frank-wolfe methods arXiv:1710.10770 (2021)
Wolfe, P.: Convergence theory in nonlinear programming. Integer and Nonlinear Programming (1970)
Yuan, X., Huang, W., Absil, P.A., Gallivan, K.: A riemannian limited-memory bfgs algorithm for computing the matrix geometric mean. Procedia Computer Science 80, 2147–2157 (2016)
Yuan, X., Huang, W., Absil, P.A., Gallivan, K.A.: A Riemannian quasi-Newton method for computing the Karcher mean of symmetric positive definite matrices. Florida State University (FSU17-02) (2017)
Zhang, H., Reddi, S., Sra, S.: Fast stochastic optimization on Riemannian manifolds. In: Advances in Neural Information Processing Systems (NIPS) (2016)
Zhang, H., Sra, S.: First-order methods for geodesically convex optimization. In: Conference on Learning Theory (COLT) (2016)
Zhang, T.: A majorization-minimization algorithm for computing the Karcher mean of positive definite matrices. SIAM J. Matrix Anal. Appl. 38(2), 387–400 (2017)
Zhang, T., Wiesel, A., Greco, M.S.: Multivariate generalized Gaussian distribution: Convexity and graphical models. Signal Processing, IEEE Transactions on 61(16), 4141–4148 (2013)
Acknowledgements
The authors thank Charles Fefferman for his helpful comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
SS acknowledges support from NSF-IIS-1409802. This work was partially done during a visit of MW at MIT supported by a Dean’s grant from the Princeton University Graduate School.
Appendices
A Approximately solving the Riemannian “linear” oracle
We want to prove the following lemma, stated in the main text:
Lemma 8
For a steps size \(\eta \in (0,1)\) and accuracy \(\delta \), we have
Proof
We use again the notation \(Y=\gamma _{XZ'}(\eta )\) for a point on the geodesic joining X and \(Z'\). By Lemma 2, we have
By construction, we have
Inserting this above, the claim follows as
\(\square \)
B Non-convex Euclidean Frank-Wolfe
We make a short digression here to mention nonconvex Euclidean Frank-Wolfe (EFW) as a potential alternative approach to solving (18). Indeed, the constraint set therein is not only g-convex, it is also convex in the usual sense. Thus, one can also apply an EFW scheme to solve (18), albeit with a slower convergence rate. In general, a g-convex set \(\mathcal {X}\) need not be Euclidean convex, so this observation does not always apply.
EFW was recently analyzed in [35]; the convergence rate reported below adapts one of its main results. The key difference, however, is that due to g-convexity, we can translate the local result of [35] into a global one for problem (18).
Theorem 6
(Convergence FW-gap ([35])) Define \({\tilde{G}}_k := \min _{0\le k\le K} G(X_k)\), where \(G(X_k)=\max _{Z_k \in \mathcal {X}} \left\langle {Z_k - X_k},\, {- \nabla \phi (X_k)} \right\rangle \) is the FW-gap (i.e., measure of convergence) at \(X_k\). Define the curvature constant
Then, after K iterations, EFW satisfies \({\tilde{G}}_K \le \frac{\max \; \lbrace 2 h_0, M_\phi \rbrace }{\sqrt{K+1}}\).
The proof (a simple adaption of [35]) is similar to that of Theorem 3; therefore, we omit it here. Finally, to implement EFW, we need to also efficiently implement its linear oracle. Theorem 7 below shows how to; the proof is similar to that of Theorem 4. It is important to note that this linear oracle involves solving a simple SDP, but it is unreasonable to require the use of an SDP solver at each iteration. Theorem 7 thus proves to be crucial, because it yields an easily computed closed-form solution.
Theorem 7
Let \(L, U \in \mathbb {P}_d\) such that \(L \prec U\) and \(S \in \mathbb {H}_d\) is arbitrary. Let \(U-L=P^*P\), and \(PSP^*=Q\varLambda Q^*\). Then, the solution to
is given by \(Z = L + P^*Q[-{{\,\mathrm{sgn}\,}}(\varLambda )]_+Q^*P\).
Proof
First, shift the constraint to \(0 \preceq X-L \preceq U-L\); then factorize \(U-L=P^*P\), and introduce a new variable \(Y=X-L\). Therewith, problem (49) becomes
If \(L=U\), then clearly \(P=0\), and \(X=L\) is the solution. Assume thus, \(L \prec U\), so that P is invertible. Thus, the above problem further simplifies to
Introduce another variable \(Z=P^*YP\) and use circularity of trace to now write
To obtain the optimal Z, first write the eigenvalue decomposition
Lemma 4 implies that the trace will be maximized when the eigenvectors of \(PSP^*\) and Z align and their eigenvalues match up. Since \(0 \preceq Z \preceq I\), we therefore see that \(Z=QDQ^*\) is an optimal solution, where D is diagonal with entries
Undoing the variable substitutions we obtain \(X=L+P^*Q[-{{\,\mathrm{sgn}\,}}(\varLambda )]_+Q^*P\) as desired. \(\square \)
Remark 4
Computing the optimal X requires 1 Cholesky factorization, 5 matrix multiplications, and 1 eigenvector decomposition. The theoretical complexity of the Euclidean Linear Oracle can therefore be estimated as \(O(N^3)\). On our machine, eigenvector decomposition is approximately 8–12 times slower than matrix multiplication. So the total flop count is approximately \(\approx \frac{1}{3} N^3 + 5\times 2N^3 + 20N^3 \approx 33N^3\).
An implementation of EFW for the computation of Riemannian centroids is shown in Algorithm 4. Experimental results for EFW in comparison with RFW and state-of-the-art Riemannian optimization methods can be found in the main text (see Sect. 6.2.1).

C Generating Positive Definite Matrices
For testing our methods in the well-conditioned regime, we generate matrices \(\lbrace A_i \rbrace _{i=1}^n \in {\mathbb {P}}_d\) by sampling real matrices of dimension d uniformly at random \(A_i \sim {\mathcal {U}}({\mathbb {R}}^{d \times d})\) and multiplying each with its transpose \(A_i \leftarrow A_i A_i^T\). This gives well-conditioned, positive definite matrices. Furthermore, we sample m matrices \(U_i \sim {\mathcal {U}}({\mathbb {R}}^{d \times d})\) with a rank deficit, i.e. \(\mathrm{rank}(U)<d\). Then, setting \(B_i \leftarrow \delta I + U_i U_i^T\) with \(\delta \) being small yields ill-conditioned matrices.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weber, M., Sra, S. Riemannian Optimization via Frank-Wolfe Methods. Math. Program. 199, 525–556 (2023). https://doi.org/10.1007/s10107-022-01840-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01840-5