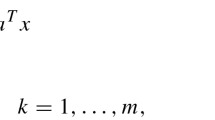Abstract
This paper studies an extended trust region subproblem (eTRS) in which the trust region intersects the unit ball with \(m\) linear inequality constraints. When \(m=0,\,m = 1\), or \(m = 2\) and the linear constraints are parallel, it is known that the eTRS optimal value equals the optimal value of a particular convex relaxation, which is solvable in polynomial time. However, it is also known that, when \(m \ge 2\) and at least two of the linear constraints intersect within the ball, i.e., some feasible point of the eTRS satisfies both linear constraints at equality, then the same convex relaxation may admit a gap with eTRS. This paper shows that the convex relaxation has no gap for arbitrary \(m\) as long as the linear constraints are non-intersecting.
Similar content being viewed by others
References
Barvinok, A.: Problems of distance geometry and convex properties of quadratic maps. Discrete Comput. Geom. 13, 189–202 (1995)
Burer, S., Anstreicher, K.: Second-order cone constraints for extended trust-region subproblems. University of Iowa (March 2011). Revised July 2012 and Nov 2012. To appear in SIAM J. Optim.
Celis, M.R., Dennis, J.E., Tapia, R.A.: A trust region strategy for nonlinear equality constrained optimization. In: Numerical Optimization, vol. 1984, pp. 71–82 (Boulder, Colo., 1984). SIAM, Philadelphia, PA (1985)
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. MPS/SIAM Series on Optimization. SIAM, Philadelphia, PA (2000)
Fu, M., Luo, Z.-Q., Ye, Y.: Approximation algorithms for quadratic programming. J. Comb. Optim. 2, 29–50 (1998)
Gould, N.I.M., Lucidi, S., Roma, M., Toint, P.L.: Solving the trust-region subproblem using the Lanczos method. SIAM J. Optim. 9(2), 504–525 (1999). (electronic)
Moré, J.J., Sorensen, D.C.: Computing a trust region step. SIAM J. Sci. Stat. Comput. 4(3), 553–572 (1983)
Pataki, G.: On the rank of extreme matrices in semidefinite programs and the multiplicity of optimal eigenvalues. Math. Oper. Res. 23, 339–358 (1998)
Pong, T., Wolkowicz, H.: The generalized trust region subproblem. University of Waterloo, Waterloo, Ontario (2012)
Rendl, F., Wolkowicz, H.: A semidefinite framework for trust region subproblems with applications to large scale minimization. Math. Program. 77(2, Ser. B):273–299 (1997).
Sherali, H.D., Adams, W.P.: A Reformulation-Linearization Technique for Solving Discrete and Continuous Nonconvex Problems. Kluwer, Dordrecht (1997)
Sturm, J.F., Zhang, S.: On cones of nonnegative quadratic functions. Math. Oper. Res. 28(2), 246–267 (2003)
Ye, Y.: A new complexity result on minimization of a quadratic function with a sphere constraint. In: Floudas, C., Pardalos, P. (eds.) Recent Advances in Global Optimization. Princeton University Press, Princeton, NJ (1992)
Ye, Y., Zhang, S.: New results on quadratic minimization. SIAM J. Optim. 14(1), 245–267 (2003). (electronic)
Acknowledgments
The authors are in debt to two anonymous referees who provided detailed suggestions that have improved the paper immensely. The authors would also like to thank Kurt Anstreicher for numerous discussions and for suggesting first that the case \(m=2\) might be extensible to arbitrary \(m\).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Burer, S., Yang, B. The trust region subproblem with non-intersecting linear constraints. Math. Program. 149, 253–264 (2015). https://doi.org/10.1007/s10107-014-0749-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-014-0749-1
Keywords
- Trust-region subproblem
- Second-order cone programming
- Semidefinite programming
- Nonconvex quadratic programming