On error reduction by the symmetric rejection method in multi-stage biometric verification systems

Abstract

A multi-stage biometric verification system serially activates its verifiers and improves performance-cost trade-off by allowing users to submit a subset of the available biometrics. In the heart of a verifier in multi-stage systems lies the concept of ‘reject option’ where a reject region is used to identify a bad quality test sample. If the match-score falls inside the reject region, no binary (genuine/impostor) decision is made in the current stage and the verifier in the next stage is activated. Recent studies have demonstrated a significant promise of the ‘symmetric rejection method’ in choosing a suitable reject region for multi-stage verification systems. In this paper, we delve into the symmetric rejection method to gain more insights into its error reduction capabilities. Specifically, we develop a theory which mathematically proves that the symmetric rejection method reduces the false accept rate and false reject rate. Then, we empirically validate our theory. Results show that the symmetric rejection method significantly reduces the error rates, both the false accept rate and false reject rate.

Appendix A Proofs of Lemma 1 and Lemma 2

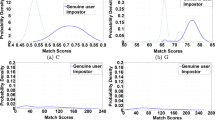
In the proofs of Lemma 1 and Lemma 2, we assume that $f_G(x)$ is monotonically decreasing inside the confusion region and $f_I(y)$ is monotonically increasing inside the confusion region. For example, in Fig. 6, $f_G(x)$ and $f_I(y)$ in (a), (b), (c), and (d) follow the assumption. However, $f_G(x)$ and $f_I(y)$ in (e) do not follow the assumption because there are ups and downs inside the confusion region $E_{1}E_{2}$.

While the above assumption simplifies our proofs, we note that our assumption is true for a wide range of distributions, including Gaussian, certain parameters of beta, binomial, and beta-binomial, and Gaussian mixture model (except when a mode is inside the confusion region). The abovementioned distributions have also been used in various studies to model score distributions of various biometric modalities (see [35,36,37,38,39]).

The sole purpose of the above assumption is to prove Lemmas 1 and 2. It is not required in the formulation of the symmetric rejection method. Hence, irrespective of this assumption, the symmetric rejection method is applicable in multi-stage biometric verification systems.

Fig. 6

Examples of $\{f_{G}(x), f_{I}(y)\}$ following/not following the assumption that $f_G(x)$ is monotonically decreasing and $f_I(y)$ is monotonically increasing inside the confusion region $E_{1}E_{2}$. $f_{G}(x)$ and $f_{I}(y)$ in (a), (b), (c), and (d) follow the assumption. However, $f_{G}(x)$ and $f_{I}(y)$ in (e) do not follow the assumption because there are ups and downs in the confusion region $E_{1}E_{2}$

Proof for Lemma1: Below, we show that $FRR^{r}_i<EER_i$. The proof of $FAR^{r}_i<EER_i$ is similar.

First, we introduce two notations. Let PQ be any region in the scoreline [Z, O]. Then, $P_{G,PQ}$ refers to the proportion of genuine scores in PQ, which is calculated by (the number of genuine scores in PQ)/(total number of genuine scores). Similarly, $P_{I,PQ}$ refers to the proportion of impostor scores in PQ, which is calculated by (the number of impostor scores in PQ)/(total number of impostor scores).

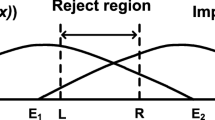
We use Fig. 7 to explain the proof. In Fig. 7, let genuine scores and impostor scores originate from verifier $v_i$, AC be the reject region, $E_1E_2$ be the confusion region, and B be the threshold where $EER_i$ occurs.

Fig. 7

Explaining Lemma 1. AC is the reject region, $ZE_2$ is the genuine score region, $E_1O$ is the impostor score region, $E_1E_2$ is the confusion region, and B is the EER-threshold

Using (4), false reject rate obtained with the symmetric rejection method,

$$\begin{aligned} FRR^{r}_i&=\frac{\#\text { of genuine scores in } CE_2}{\text {Total} \# \text {of genuine scores}-\#\text { of genuine scores in} AC} \nonumber \\&=\frac{\text {Proportion of genuine scores in } CE_2}{1-\text {Proportion of genuine scores in} AC} \nonumber \\&=\frac{P_{G,CE_{2}}}{1-P_{G,AC}} \nonumber \\&=\frac{P_{G,CE_{2}}}{1-P_{G,AB}-P_{G,BC}}. \end{aligned}$$

(A1)

$$\begin{aligned}&\hbox {Let} \ \ \ \ \frac{P_{G,BE_{2}}}{P_{G,BC}} = \mu .&\end{aligned}$$

(A2)

Because C lies inside $(B,E_{2}]$, it follows that $\mu \ge 1$. From (A2) we get, $P_{G,BC}=P_{G,BE_{2}}/\mu$. Hence, we can present the numerator on the right side of (A1) as follows:

$$\begin{aligned} P_{G,CE_{2}}=P_{G,BE_{2}}-P_{G,BC}=P_{G,BE_{2}}-\frac{P_{G,BE_{2}}}{\mu }=\frac{(\mu -1)P_{G,BE_{2}}}{\mu }. \end{aligned}$$

Therefore, we can rewrite (A1) as:

$$\begin{aligned} FRR^{r}_i=\frac{(\mu -1)P_{G,BE_{2}}}{\mu -P_{G,BE_{2}}-\mu P_{G,AB}}. \end{aligned}$$

(A3)

Because $EER_i$ occurs at threshold B,

$$\begin{aligned} EER_i=P_{I, E_{1}B}=P_{G, BE_{2}}. \end{aligned}$$

(A4)

We will prove that $FRR^{r}_i<EER_i$. For contradiction, we assume that $FRR^{r}_i \ge EER_i$. This implies–

$$\frac{(\mu -1)P_{G,BE_{2}}}{\mu -P_{G,BE_{2}}-\mu P_{G,AB}} \ge P_{G,BE_{2}}.$$

After algebraic manipulation we get,

$$\begin{aligned}&\mu -1 \ge \mu -P_{G,BE_{2}}-\mu P_{G,AB} \nonumber \\ \text {or, }&1-P_{G,BE_{2}} \le \mu P_{G,AB}. \end{aligned}$$

(A5)

Because $ZE_2$ contains all genuine scores, $P_{G,ZE_{2}}=1$. Hence, $1-P_{G,BE_{2}}=P_{G,ZE_{2}}-P_{G,BE_{2}}=P_{G,ZB}$. Therefore, we can rewrite (A5) as follows:

$$\begin{aligned} P_{G,ZB} \le \mu P_{G,AB}. \end{aligned}$$

(A6)

Because $f_{G}(x)$ is monotonically decreasing and $f_{I}(y)$ is monotonically increasing inside $E_{1}B$, the following statement is true:

$$\begin{aligned} \frac{P_{G,E_{1}B}}{P_{G,AB}} \ge \frac{P_{I,E_{1}B}}{P_{I,AB}}. \end{aligned}$$

(A7)

From (A4), $P_{I,E_{1}B}=P_{G,BE_{2}}$ and using the symmetric rejection method, $P_{I,AB}=P_{G,BC}$. Then,

$$\begin{aligned} \frac{P_{I,E_{1}B}}{P_{I,AB}}=\frac{P_{G,BE_{2}}}{P_{G,BC}} = \mu . \end{aligned}$$

Hence, we can rewrite (A7) as follows:

$$\begin{aligned}&\frac{P_{G,E_{1}B}}{P_{G,AB}} \ge \mu \\ \text {or, }&P_{G,E_{1}B} \ge \mu P_{G,AB}. \end{aligned}$$

Because $E_{1}B$ is a part of ZB (see Fig. 7), $P_{G,ZB}>P_{G,E_{1}B}$. Because $P_{G,ZB}>P_{G,E_{1}B}$ and $P_{G,E_{1}B} \ge \mu P_{G,AB}$, it follows that $P_{G,ZB} > \mu P_{G,AB}$. However, this contradicts (A6). Therefore, we conclude that $FRR^{r}_i<EER_i$.

Proof for Lemma 2: We use Fig. 8 to explain the proof.

Fig. 8

Illustration of Lemma 2. $A_1C_1$ and $A_2C_2$ are two reject regions such that $A_2C_2$ is greater than $A_1C_1$. $ZE_2$ is the genuine score region, $E_1O$ is the impostor score region, $E_1E_2$ is the confusion region, and B is the EER-threshold

In Fig. 8, B is the EER-threshold and reject region $A_2C_2$ is greater than reject region $A_1C_1$. We need to prove that

$$\begin{aligned} \frac{P_{G,BC_1}}{P_{G,A_1C_1}}>\frac{P_{G,BC_2}}{P_{G,A_2C_2}}. \end{aligned}$$

(A8)

We can rewrite (A8) as follows:

$$\begin{aligned} \frac{P_{G,BC_1}}{P_{G,BC_2}}>\frac{P_{G,A_1C_1}}{P_{G,A_2C_2}}. \end{aligned}$$

(A9)

Now we will prove that (A9) is true.

Because $A_2C_2$ is greater than $A_1C_1$, $P_{G,BC_2}>P_{G,BC_1}$. Let

$$\begin{aligned} P_{G,BC_2}=\rho P_{G,BC_1}, \end{aligned}$$

(A10)

where $\rho$ is a real number greater than 1.

Because $f_{G}(x)$ is monotonically decreasing and $f_{I}(y)$ is monotonically increasing inside the confusion region, when we increase the width of a reject region, the proportion of genuine scores on the left side increases at a higher rate than the proportion of genuine scores on the right. Hence, we can write

$$\begin{aligned} P_{G,A_2B}=(\rho +\epsilon ) P_{G,A_1B}, \end{aligned}$$

(A11)

where $\epsilon$ is a real number greater than 0.

Now,

$$\begin{aligned} \frac{P_{G,A_1C_1}}{P_{G,A_2C_2}} = \frac{P_{G,A_1B}+P_{G,BC_1}}{P_{G,A_2B}+P_{G,BC_2}}. \end{aligned}$$

(A12)

Using (A10) and (A11), we can rewrite (A12) as follows:

$$\begin{aligned} \frac{P_{G,A_1C_1}}{P_{G,A_2C_2}} = \frac{P_{G,A_1B}+P_{G,BC_1}}{\rho (P_{G,A_1B}+P_{G,BC_1})+\epsilon P_{G,A_1B}}. \end{aligned}$$

(A13)

Because $\epsilon P_{G,A_1B}>0$, the right-hand side of (A13) is less than $\frac{1}{\rho }$. Hence, we can rewrite (A13) as follows:

$$\begin{aligned} \frac{P_{G,A_1C_1}}{P_{G,A_2C_2}} < \frac{1}{\rho }. \end{aligned}$$

(A14)

However, using (A10) we get

$$\begin{aligned} \frac{P_{G,BC_1}}{P_{G,BC_2}} = \frac{1}{\rho }. \end{aligned}$$

(A15)

From (A14) and (A15) we get

$$\begin{aligned} \frac{P_{G,BC_1}}{P_{G,BC_2}} > \frac{P_{G,A_1C_1}}{P_{G,A_2C_2}}. \end{aligned}$$