Finding patterns in the degree distribution of real-world complex networks: going beyond power law | Pattern Analysis and Applications Skip to main content
Springer Nature Link
Log in

Finding patterns in the degree distribution of real-world complex networks: going beyond power law

  • Industrial and Commercial Application
  • Published:
Pattern Analysis and Applications Aims and scope Submit manuscript

Abstract

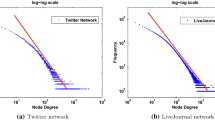
The most important structural characteristics in the study of large-scale real-world complex networks in pattern analysis are degree distribution. Empirical observations on the pattern of the real-world networks have led to the claim that their degree distributions follow, in general, a single power law. However, a closer observation, while fitting, shows that the single power-law distribution is often inadequate to meet the data characteristics properly. Since the degree distribution in the log–log scale actually displays, under inspection, two different slopes unlike what happens while fitting with the single power law. These two slopes with a transition in between closely resemble the pattern of the sigmoid function. This motivates us to derive a novel double power-law distribution for accurately modeling the real-world networks based on the sigmoid function. The proposed modeling approach further leads to the identification of a transition degree which, it has been demonstrated, may have a significant implication in analyzing the complex networks. The applicability, as well as effectiveness of the proposed methodology, is shown using rigorous experiments and also validated using statistical tests.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Adamic LA, Huberman BA (2000) Power-law distribution of the world wide web. Science 287(5461):2115–2115

    Article  Google Scholar 

  2. Adamic LA, Lukose RM, Puniyani AR, Huberman BA (2001) Search in power-law networks. Phys Rev E 64(4):046135

    Article  Google Scholar 

  3. Albert R, Barabási AL (2002) Statistical mechanics of complex networks. Rev Mod Phys 74(1):47

    Article  MathSciNet  MATH  Google Scholar 

  4. Albert R, Jeong H, Barabási AL (2000) Error and attack tolerance of complex networks. Nature 406(6794):378

    Article  Google Scholar 

  5. Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000) Classes of small-world networks. Proc Natl Acad Sci 97(21):11149–11152

    Article  Google Scholar 

  6. Barabasi AL (2005) The origin of bursts and heavy tails in human dynamics. Nature 435(7039):207

    Article  Google Scholar 

  7. Barabási AL, Albert R (1999) Emergence of scaling in random networks. Science 286(5439):509–512

    Article  MathSciNet  MATH  Google Scholar 

  8. Bauke H (2007) Parameter estimation for power-law distributions by maximum likelihood methods. Eur Phys J B 58(2):167–173

    Article  Google Scholar 

  9. Bollobás B, Riordan OM (2003) Mathematical results on scale-free random graphs. In: Bornholdt S, Schuster HG (eds) Handbook of graphs and networks: from the genome to the internet. Wiley, London, pp 1–34

    MATH  Google Scholar 

  10. Broder A (2000) A. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, R. Stata, A. Tomkins, and J. Wiener, Comput. Netw. 33, 309. Comput Netw 33:309

    Article  Google Scholar 

  11. Chattopadhyay S, Murthy C, Pal SK (2014) Fitting truncated geometric distributions in large scale real world networks. Theor Comput Sci 551:22–38

    Article  MathSciNet  MATH  Google Scholar 

  12. Choi DJ (1992) On a generalization of the hurwitz zeta function \(f (s, a)\). Indian J Pure Appl Math 23(2):83–91

    MathSciNet  MATH  Google Scholar 

  13. Clauset A, Young M, Gleditsch KS (2007) On the frequency of severe terrorist events. J Confl Resolut 51(1):58–87

    Article  Google Scholar 

  14. Clauset A, Shalizi CR, Newman ME (2009) Power-law distributions in empirical data. SIAM Rev 51(4):661–703

    Article  MathSciNet  MATH  Google Scholar 

  15. Coelho R, Richmond P, Barry J, Hutzler S (2008) Double power laws in income and wealth distributions. Phys A Stat Mech Appl 387(15):3847–3851

    Article  MathSciNet  Google Scholar 

  16. Goldstein ML, Morris SA, Yen GG (2004) Problems with fitting to the power-law distribution. Eur Phys J B Condens Matter Complex Syst 41(2):255–258

    Article  Google Scholar 

  17. Guo K, Guo W, Chen Y, Qiu Q, Zhang Q (2015) Community discovery by propagating local and global information based on the mapreduce model. Inf Sci 323:73–93

    Article  MathSciNet  Google Scholar 

  18. Huberman BA (1999) Ba huberman and la adamic. Nature (London) 401:131

    Article  Google Scholar 

  19. Kleinberg JM, Kumar R, Raghavan P, Rajagopalan S, Tomkins AS (1999) The web as a graph: measurements, models, and methods. In: International computing and combinatorics conference. Springer, pp 1–17

  20. Leskovec J, Krevl A (2014) SNAP Datasets: Stanford large network dataset collection. http://snap.stanford.edu/data

  21. Leskovec J, Chakrabarti D, Kleinberg J, Faloutsos C, Ghahramani Z (2010) Kronecker graphs: an approach to modeling networks. J Mach Learn Res 11(Feb):985–1042

    MathSciNet  MATH  Google Scholar 

  22. Liu Y, Li C, Tang WK, Zhang Z (2012) Distributed estimation over complex networks. Inf Sci 197:91–104

    Article  MATH  Google Scholar 

  23. Muchnik L, Pei S, Parra LC, Reis SD, Andrade JS Jr, Havlin S, Makse HA (2013) Origins of power-law degree distribution in the heterogeneity of human activity in social networks. Sci Rep 3:1783

    Article  Google Scholar 

  24. Newman ME (2001) The structure of scientific collaboration networks. Proc Natl Acad Sci 98(2):404–409

    Article  MathSciNet  MATH  Google Scholar 

  25. Newman ME (2003) The structure and function of complex networks. SIAM Rev 45(2):167–256

    Article  MathSciNet  MATH  Google Scholar 

  26. Newman ME (2005) Power laws, Pareto distributions and Zipf’s law. Contemp Phys 46(5):323–351

    Article  Google Scholar 

  27. Newman ME, Strogatz SH, Watts DJ (2001) Random graphs with arbitrary degree distributions and their applications. Phys Rev E 64(2):026118

    Article  Google Scholar 

  28. Pennock DM, Flake GW, Lawrence S, Glover EJ, Giles CL (2002) Winners don’t take all: characterizing the competition for links on the web. Proc Natl Acad Sci 99(8):5207–5211

    Article  MATH  Google Scholar 

  29. Richmond P, Hutzler S, Coelho R, Repetowicz P (2006) A review of empirical studies and models of income distributions in society. Wiley, Berlin

    Book  Google Scholar 

  30. Rossi RA, Ahmed NK (2015) The network data repository with interactive graph analytics and visualization. In: Proceedings of the twenty-ninth AAAI conference on artificial intelligence. http://networkrepository.com

  31. Sala A, Zheng H, Zhao BY, Gaito S, Rossi GP (2010) Brief announcement: revisiting the power-law degree distribution for social graph analysis. In: Proceedings of the 29th ACM SIGACT-SIGOPS symposium on Principles of distributed computing. ACM, pp 400–401

  32. Seal H (1952) The maximum likelihood fitting of the discrete Pareto law. J Inst Actuar 78(1):115–121

    Article  MATH  Google Scholar 

  33. Seshadri M, Machiraju S, Sridharan A, Bolot J, Faloutsos C, Leskove J (2008) Mobile call graphs: beyond power-law and lognormal distributions. In: Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, pp 596–604

  34. Song Y, Zhang C, Wu M (2010) The study of human behavior dynamics based on blogosphere. In: 2010 International conference on web information systems and mining (WISM), vol 1. IEEE, pp 87–91

  35. Sun PG, Gao L, Han SS (2011) Identification of overlapping and non-overlapping community structure by fuzzy clustering in complex networks. Inf Sci 181(6):1060–1071

    Article  MATH  Google Scholar 

  36. Toda AA (2012) The double power law in income distribution: explanations and evidence. J Econ Behav Organ 84(1):364–381

    Article  Google Scholar 

  37. Yang J, Leskovec J (2015) Defining and evaluating network communities based on ground-truth. Knowl Inf Syst 42(1):181–213

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial assistance received from Indian Statistical Institute (I. S. I.) and Visvesvaraya PhD Scheme awarded by the Government of India.

Author information

Authors and Affiliations

  1. Machine Intelligence Unit, Indian Statistical Institute, 203 - Barrackpore Trunk Road, Kolkata, India

    Swarup Chattopadhyay & Kuntal Ghosh

  2. Department of Computer Science and Technology, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711 103, India

    Swarup Chattopadhyay & Asit K. Das

Authors
  1. Swarup Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Asit K. Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kuntal Ghosh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Swarup Chattopadhyay.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 1864 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chattopadhyay, S., Das, A.K. & Ghosh, K. Finding patterns in the degree distribution of real-world complex networks: going beyond power law. Pattern Anal Applic 23, 913–932 (2020). https://doi.org/10.1007/s10044-019-00820-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10044-019-00820-4

Keywords

Search

Navigation