Abstract.
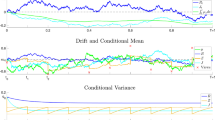
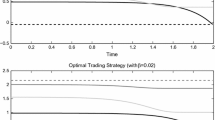
We consider a multi-stock market model where prices satisfy a stochastic differential equation with instantaneous rates of return modeled as a continuous time Markov chain with finitely many states. Partial observation means that only the prices are observable. For the investor’s objective of maximizing the expected utility of the terminal wealth we derive an explicit representation of the optimal trading strategy in terms of the unnormalized filter of the drift process, using HMM filtering results and Malliavin calculus. The optimal strategy can be determined numerically and parameters can be estimated using the EM algorithm. The results are applied to historical prices.
Similar content being viewed by others
Author information
Authors and Affiliations
Corresponding author
Additional information
Received: March 2004,
Mathematics Subject Classification (2000):
91B28, 60G44
JEL Classification:
G11
Supported by NSERC under research grant 88051 and NCE grant 30354.
Rights and permissions
About this article
Cite this article
Sass, J., Haussmann, U.G. Optimizing the terminal wealth under partial information: The drift process as a continuous time Markov chain. Finance and Stochastics 8, 553–577 (2004). https://doi.org/10.1007/s00780-004-0132-9
Issue Date:
DOI: https://doi.org/10.1007/s00780-004-0132-9