Abstract
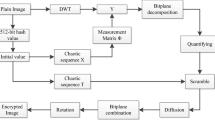
In this paper, an efficient image compression and encryption scheme combining the parameter-varying chaotic system, elementary cellular automata (ECA) and block compressive sensing (BCS) is presented. The architecture of permutation, compression and re-permutation is adopted. Firstly, the plain image is transformed by DWT, and four block matrices are gotten, and they are a low-frequency block with important information and three high-frequency blocks with less important information. Secondly, ECA is used to scramble the four sparse block matrices, which can effectively change the position of the elements in the matrices and upgrade the confusion effect of the algorithm. Thirdly, according to the importance of each block, BCS is adopted to compress and encrypt four scrambled matrices with different compression ratios. In the BCS, the measurement matrices are constructed by a parameter-varying chaotic system, and thus few parameters may produce the large measurement matrices, which may effectively reduce memory space and transmission bandwidth. Finally, the four compressed matrices are recombined into a large matrix, and the cipher image is obtained by re-scrambling it. Moreover, the initial values of the chaotic system are produced by the SHA 256 hash value of the plain image, which makes the proposed encryption algorithm highly sensitive to the original image. Experimental results and performance analyses demonstrate its good security and robustness.





















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Wu JH, Liao XF, Yang B (2018) Image encryption using 2D Henon-Sine map and DNA approach. Signal Process 153:11–23
Chai XL, Gan ZH, Yuan K, Chen YR, Liu XX (2017) A novel image encryption scheme based on DNA sequence operations and chaotic systems. Neural Comput Appl. https://doi.org/10.1007/s00521-017-2993-9
Niyat AY, Moattar MH, Torshiz MN (2017) Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt Laser Eng 90:225–237
Hua ZY, Yi S, Zhou YC (2018) Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process 144:134–144
Wang XY, Wang Q (2014) A novel image encryption algorithm based on dynamic S-boxes constructed by chaos. Nonlinear Dyn 75(3):567–576
Liu HJ, Kadir A (2015) Asymmetric color image encryption scheme using 2D discrete-time map. Signal Process 113:104–112
Ahmad M, Al Solami E, Wang XY et al (2018) Cryptanalysis of an image encryption algorithm based on combined chaos for a BAN system, and improved scheme using SHA-512 and hyperchaos. Symmetry 10(7):266
Wen WY, Zhang YS, Fang YM, Fang ZJ (2016) Image salient regions encryption for generating visually meaningful ciphertext image. Neural Comput Appl 6:1–11
Matthews R (1989) On the derivation of a chaotic encryption algorithm. Cryptologia 13(1):29–42
Wang XY, Teng L, Qin X (2012) A novel colour image encryption algorithm based on chaos. Signal Process 92(4):1101–1108
Pak C, Huang LL (2017) A new color image encryption using combination of the 1D chaotic map. Signal Process 138:129–137
Wu XJ, Kan HB, Kurths J (2015) A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl Soft Comput 37:24–39
Li CQ, Xie T, Liu Q, Cheng G (2014) Cryptanalyzing image encryption using chaotic logistic map. Nonlinear Dyn 78:1545–1551
Boriga R, Dăscălescu AC, Priescu I (2014) A new hyperchaotic map and its application in an image encryption scheme. Signal Process Image Commun 29(8):887–901
Zhang Q, Guo L, Wei XP (2013) A novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system. Optik 124(18):3596–3600
Zhou YC, Bao L, Chen CLP (2014) A new 1D chaotic system for image encryption. Signal Process 97:172–182
Liu LF, Miao SX (2017) An image encryption algorithm based on Baker map with varying parameter. Multimed Tools Appl 76(15):16511–16527
Zahmoul R, Ejbali R, Zaied M (2017) Image encryption based on new Beta chaotic maps. Opt Lasers Eng 96:39–49
Dalhoum ALA, Mahafzah BA, Awwad AA, Aldhamari I, Ortega A, Alfonseca M (2012) Digital image scrambling using 2D cellular automata. IEEE Multimedia 19(4):28–36
Madain A, Dalhoum ALA, Hiary H, Ortega A, Alfonseca M (2014) Audio scrambling technique based on cellular automata. Multimed Tools Appl 71(3):1803–1822
Wolfram S (1986) Random sequence generation by cellular automata. Adv Appl Math 7(2):123–169
Chen RJ, Horng SJ (2010) Novel SCAN-CA-based image security system using SCAN and 2-D von Neumann cellular automata. Signal Process Image Commun 25(6):413–426
Wang XY, Xu DH (2015) A novel image encryption scheme using chaos and Langton’s Ant cellular automaton. Nonlinear Dyn 79(4):2449–2456
Dalhoum ALA, Madain A, Hiary H (2016) Digital image scrambling based on elementary cellular automata. Multimed Tools Appl 75(24):17019–17034
Ping P, Wu JJ, Mao YC, Xu F, Fan JY (2018) Design of image cipher using life-like cellular automata and chaotic map. Signal Process 150:233–247
Zhou NR, Pan SM, Cheng S, Zhou ZH (2016) Image compression–encryption scheme based on hyper-chaotic system and 2D compressive sensing. Opt Laser Technol 82:121–133
Liu XY, Cao YP, Lu P, Lu X, Li Y (2013) Optical image encryption technique based on compressed sensing and Arnold transformation. Optik 124(24):6590–6593
Zhou NR, Zhang AD, Zheng F, Gong LH (2014) Novel image compression –encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing. Opt Laser Technol 62:152–160
Zhang YS, Zhou JT, Chen F, Zhang LY, Xiao D, Chen B, Liao XF (2016) A block compressive sensing based scalable encryption framework for protecting significant image regions. Int J Bifurcat Chaos 26(11):1234–1247
Zhou NR, Li HL, Wang D, Pan SM, Zhou ZH (2015) Image compression and encryption scheme based on 2D compressive sensing and fractional Mellin transform. Opt Commun 343:10–21
Chai XL, Gan ZH, Chen YR, Zhang YS (2017) A visually secure image encryption scheme based on compressive sensing. Signal Process 134:35–51
Chai XL, Zheng XY, Gan ZH, Han DJ, Chen YR (2018) An image encryption algorithm based on chaotic system and compressive sensing. Signal Process 148:124–144
Hu GQ, Xiao D, Wang Y, Xiang T (2017) An image coding scheme using parallel compressive sensing for simultaneous compression-encryption applications. J Vis Commun Image R 44:116–127
Liang YR, Wu JH (2015) Image encryption based on compressive sensing and variable-parameter chaotic mapping. J Optoelectron Laser 26(3):605–610
Baranovsky A, Daems D (1995) Design of one-dimensional chaotic maps with prescribed statistical properties. Int J Bifurcat Chaos 5(6):1585–1598
Enayatifar R, Sadaei HJ, Abdullah AH, Lee M, Isnin IF (2015) A novel chaotic based image encryption using a hybrid model of deoxyribonucleic acid and cellular automata. Opt Lasers Eng 71:33–41
Li XW, Xiao D, Wang QH (2018) Error-free holographic frames encryption with CA pixel-permutation encoding algorithm. Opt Lasers Eng 100:200–207
Niyat AY, Moattar MH, Torshiz MN (2017) Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt Lasers Eng 90:225–237
Chen TH, Zhang M, Wu JH, Yuen C, Tong Y (2016) Image encryption and compression based on kronecker compressed sensing and elementary cellular automata scrambling. Opt Laser Technol 84:118–133
Hortensius PD, McLeod RD, Card HC (1989) Parallel random number generation for VLSI systems using cellular automata. IEEE Trans Comput 38:1466–1473
Nandi S, Kar BK, Chaudhuri PP (1994) Theory and applications of cellular automata in cryptography. IEEE Trans Comput 43:1346–1357
Tomassini M, Perrenoud M (2000) Stream ciphers with one- and two-dimensional cellular automata. In: Parallel problem solving from nature-PPSN VI, LNCS, vol 1917, pp 722–731
Xiao D, Cai HK, Zheng HY (2015) A joint image encryption and watermarking algorithm based on compressive sensing and chaotic map. Chin Phys B 24(6):198–206
Ponnaian D, Chandranbabu K (2017) Cryptanalysis of an image compression–encryption algorithm and a modified scheme using compressive sensing. Optik 147:263–276
Donoho DL (2006) Compressed sensing. IEEE T Inform Theory 52(4):1289–1306
Chen JX, Zhang Y, Qi L, Fu C, Xu LS (2018) Exploiting chaos-based compressed sensing and cryptographic algorithm for image encryption and compression. Opt Laser Technol 99:238–248
Wu XG, Tang SJ, Yang PL, Xiang CC, Zheng X (2018) Cloud is safe when compressive: efficient image privacy protection via shuffling enabled compressive sensing. Comput Commun 117:36–45
Ma LH, Jin WM (2018) Symmetric and asymmetric hybrid cryptosystem based on compressive sensing and computer generated holography. Opt Commun 407:51–56
Liu E, Temlyakov VN (2012) The orthogonal super greedy algorithm and application in compressed sensing. IEEE T Inform Theory 58(4):2040–2047
Mohimani H, Babaie-Zadeh M, Jutten C (2009) A fast approach for overcomplete sparse decomposition based on smoothed L0 norm. IEEE T Signal Process 57(1):289–301
Unde Amit Satish, Deepthi PP (2018) Rate-distortion analysis of structured sensing matrices for block compressive sensing of images. Signal Process. Image 65:115–127
Candes EJ, Tao T (2006) Near-optimal signal recovery from random projections: universal encoding strategies? IEEE Trans Inf Theory 52:5406–5425
Gan L (2007) Block compressed sensing of natural images. In: 15th IEEE international conference on digital signal processing, pp 403–406
Hamid Safavi Seyed, Farah Torkamani-Azar (2017) Sparsity-aware adaptive block-based compressive sensing. IET. Signal Process 11:36–42
Dinh KQ, Shim HJ, Jeon B (2017) Small-block sensing and larger-block recovery in block-based compressive sensing of images. Signal Process Image 55:10–22
Tong XJ, Zhang M, Wang Z, Ma J (2016) A joint color image encryption and compression scheme based on hyper-chaotic system. Nonlinear Dyn 84(4):2333–2356
Hua ZY, Zhou YC (2017) Design of image cipher using block-based scrambling and image filtering. Inf Sci 396:97–113
Alvarez G, Li SJ (2006) Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcat Chaos 16(8):2129–2151
Rey AMD, Pastora JLH, Sánchez GR (2016) 3D medical data security protection. Expert Syst Appl 54:379–386
Guesmi R, Farah MAB, Kachouri A, Samet M (2016) A novel chaos-based image encryption using DNA sequence operation and Secure Hash Algorithm SHA-2. Nonlinear Dyn 83:1123–1136
Zhu CX (2012) A novel image encryption scheme based on improved hyperchaotic sequences. Opt Commun 285(1):29–37
Luo YL, Zhou RL, Liu JX, Cao Y, Ding XM (2018) A parallel image encryption algorithm based on the piecewise linear chaotic map and hyper-chaotic map. Nonlinear Dyn 93:1165–1181
Chai XL, Gan ZH, Yang K, Chen YR, Liu XX (2017) An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process Image 52:6–19
Xie Eric Y, Li CQ, Yu SM, Lu JH (2017) On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Process 132:150–154
Li CQ, Lin DD, Lü JH, Hao F (2018) Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE Multimedia. https://doi.org/10.1109/mmul.2018.2873472
Mirzaei O, Yaghoobi M, Irani H (2012) A new image encryption method: parallel sub-image encryption with hyper chaos. Nonlinear Dyn 67:557–566
Huang XL, Ye GD (2014) An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed Tools Appl 72(1):57–70
Zhang Q, Guo L, Wei XP (2010) Image encryption using DNA addition combining with chaotic maps. Math Comput Model 52(11–12):2028–2035
Chai XL, Gan ZH, Yuan K, Lu Y, Chen YR (2017) An image encryption scheme based on three-dimensional Brownian motion and chaotic system. Chin Phys B 26(2):99–113
Acknowledgements
All the authors are deeply grateful to the editors for smooth and fast handling of the manuscript. The authors would also like to thank the anonymous referees for their valuable suggestions to improve the quality of this paper. This work is supported by the National Natural Science Foundation of China (Grant Nos. 41571417, U1604145, 61802111, 61872125, 61871175), National Science Foundation of the United States (Grant Nos. CNS-1253424 and ECCS-1202225), Science and Technology Foundation of Henan Province of China (Grant Nos. 182102210027, 182102410051), China Postdoctoral Science Foundation (Grant Nos. 2018T110723, 2016M602235), Key Scientific Research Projects for Colleges and Universities of Henan Province (Grant No. 19A413001), CERNET NGI Technology Innovation Project (Grant No. NGII20170902) and the Research Foundation of Henan University (Grant No. xxjc20140006).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chai, X., Fu, X., Gan, Z. et al. An efficient chaos-based image compression and encryption scheme using block compressive sensing and elementary cellular automata. Neural Comput & Applic 32, 4961–4988 (2020). https://doi.org/10.1007/s00521-018-3913-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-018-3913-3