Multicriteria q-Rung orthopair fuzzy decision analysis: a novel approach based on Archimedean aggregation operators with the confidence levels | Soft Computing Skip to main content
Springer Nature Link
Log in

Multicriteria q-Rung orthopair fuzzy decision analysis: a novel approach based on Archimedean aggregation operators with the confidence levels

  • Soft computing in decision making and in modeling in economics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

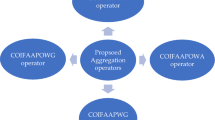
The confidence levels can reduce the influence of the unreasonable evaluation value that was given by the decision-maker on the decision-making results. The Archimedean t-norm and t-conorm (ATS) also have many advantages for the processing of uncertain data. Under this environment, the confidence q-rung orthopair fuzzy aggregation operator based on ATS is one of the most successful extensions of confidence q-rung orthopair fuzzy numbers in which we decrease the deviation caused by the subjective perspective of the decision-maker in the multicriteria group decision-making problems. In this paper, we propose weighted, ordered weighted averaging aggregation operators and weighted, ordered weighted geometric aggregation operators based on ATS, respectively. Moreover, the properties and four specific forms associated with aggregation operators are also investigated. In this study, a novel MCGDM approach is introduced by using the proposed operator. A reasonable example is proposed and compared the results that are obtained by our operators and that in the existing literature, so as to verify the rationality and flexible of our method. From the study, we concluded that the proposed method can reduce the impact of extreme data, and make decision-making results more reasonable by considering the attitudes of decision-makers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

The data used to support the finding are cited within the article.

References

  • Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    Article  Google Scholar 

  • Atanassov K (1999) Intuitionistic fuzzy sets: theory and applications, Heidelberg. Springer, Germany

    Book  Google Scholar 

  • Bai K, Zhu X, Wang J et al (2019) Power partitioned Heronian mean operators for q-rung orthopair uncertain linguistic sets with their application to multiattribute group decision making, Int J Int Syst, 1-35

  • Chen T, Li C (2010) Determining objective weights with intuitionistic fuzzy entropy measures: a comparative analysis. Inf Sci 180(21):4207–4222

    Article  Google Scholar 

  • De S, Biswas R, Roy A (2000) Some operations on intuitionistic fuzzy sets. Fuzzy Sets Syst 114(3):477–484

    Article  MathSciNet  Google Scholar 

  • Garg H (2017) Distance and similarity measure for intuitionistic multiplicative preference relation and its application. Int J Uncertain Quantification 7(2):117–133

    Article  Google Scholar 

  • Garg H (2019) Novel neutrality operation-based Pythagorean fuzzy geometric aggregation operators for multiple attribute group decision analysis. Int J Int Sys 34(10):2459–2489

    Article  Google Scholar 

  • Garg H (2017) Confidence levels based Pythagorean fuzzy aggregation operators and its application to decision-making process. Comput Math Organ Theory 23(4):546–571

    Article  Google Scholar 

  • Garg H (2016) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Int Syst 31(9):886–920

    Article  Google Scholar 

  • Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Int Syst 32(6):597–630

    Article  Google Scholar 

  • Garg H, Arora R (2018) Dual hesitant fuzzy soft aggregation operators and their application in decision-making. Cogn Comput 10(5):769–789

    Article  Google Scholar 

  • Garg H (2019) Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision-making process. Int J Int Syst 34(4):601–626

    Article  Google Scholar 

  • Joshi B, Singh A, Bhatt P et al (2018) Interval valued q-rung orthopair fuzzy sets and their properties. J Int Fuzzy Syst 35(5):5225–5230

    Google Scholar 

  • Joshi R, Kumar S (2019) Jensen-Tsalli’s intuitionistic fuzzy divergence measure and its applications in medical analysis and pattern recognition. Int J Uncertain, Fuzziness Knowl-Based Syst 27(1):145–169

    Article  MathSciNet  Google Scholar 

  • Joshi B, Gegov A (2020) Confidence levels q-rung orthopair fuzzy aggregation operators and its applications to MCDM problems. Int J Intell Syst 35(1):125–149

  • Ju Y, Wang A, Ma J et al (2019) Some q-rung orthopair fuzzy 2-tuple linguistic Muirhead mean aggregation operators and their applications to multiple-attribute group decision making, Int J Intell Syst, 1–30

  • Klement EP, Mesiar R (eds) (2005) Logical, algebraic, analytic, and probabilistic aspects of triangular norms. Elsevier, USA, New York

    MATH  Google Scholar 

  • Li J, Zhang X, Gong Z (2018) Aggregating of interval-valued intuitionistic uncertain linguistic variables based on Archimedean t-norm and it applications in group decision makings. J Comput Anal Appl 24(5):874–885

    MathSciNet  Google Scholar 

  • Liu Z, Wang S, Liu P (2018) Multiple attribute group decision making based on q-rung orthopair fuzzy Heronian mean operators. Int J Intell Syst 33(12):2341–2363

    Article  Google Scholar 

  • Liu X, Xu Y, Montes R et al (2019) Analysis of self-confidence indices-based additive consistency for fuzzy preference relations with self-confidence and its application in group decision making. Int J Intell Syst 34(5):920–946

    Article  Google Scholar 

  • Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33:259–280

    Article  Google Scholar 

  • Liu P, Chen S, Wang P (2018) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators, IEEE Trans Syst Man Cybern-Syst 1–16

  • Liu P, Chen S (2017) Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans Syst Man Cybern-Syst 47(9):2514–2530

    Google Scholar 

  • Liu P, Liu J (2018) Some q-rung orthopair fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst 33(2):315–347

    Article  Google Scholar 

  • Li C, Rodriguez R, Martinez L et al (2019) Consensus building with individual consistency control in group decision making. IEEE Trans Fuzzy Syst 27(2):319–332

    Article  Google Scholar 

  • Liu P, Gao H (2019) Some intuitionistic fuzzy power Bonferroni mean operators in the framework of Dempster-Shafer theory and their application to multicriteria decision making. Appl Soft Comput 85:139–177

    Google Scholar 

  • Morente-Molinera J, Wu X, Morfeq A et al (2020) A novel multi-criteria group decision-making method for heterogeneous and dynamic contexts using multi-granular fuzzy linguistic modelling and consensus measures. Inform Fusion 53:240–250

    Article  Google Scholar 

  • Muhammad M, Humaira K, etc (2020) T-Spherical fuzzy Einstein hybrid aggregation operators and their applications in multi-attribute decision making problems, Symmetry, 12, 365; https://doi.org/10.3390/sym12030365

  • Peng X, Dai J, Garg H (2018) Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int J Intell Syst 33(11):2255–2282

    Article  Google Scholar 

  • Qin Q, Liang F, Li L et al (2017) A TODIM-based multi-criteria group decision making with triangular intuitionistic fuzzy numbers. App Soft Comput 55:93–107

    Article  Google Scholar 

  • M, Hamid MT, Afzal D, ect, (2021) Multi-criteria decision making in robotic agri-farming with q-rung orthopair m-polar fuzzy sets. PLoS ONE 16(2):e024685. https://doi.org/10.1371/journal.pone.0246485

  • Riaz M, Hafiz MAF, Humaira Kalsoom, ect (2020) A robust q-Rung orthopair fuzzy Einstein prioritized aggregation operators with application towards MCGDM, Symmetry 12:1058. https://doi.org/10.3390/sym12061058

  • Riaz M, Ayesha R, Humaira K, ect (2020) q-Rung orthopair fuzzy geometric aggregation operators based on generalized and group-generalized parameters with application to water loss management, Symmetry, 12, 1236; https://doi.org/10.3390/sym12081236

  • Rodriguez R, Martinez L, Herrera F (2012) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20(1):109–119

    Article  Google Scholar 

  • Shi Z, Gong Z, Shao Y (2012) A novel similarity measure of intuitionistic fuzzy sets induced by triangular norm, In 2012 international conference on machine learning and cybernetics, 233–237

  • Sun B, Zhou X, Lin N (2020) Diversified binary relation-based fuzzy multigranulation rough set over two universes and application to multiple attribute group decision making. Inf Fusion 55:91–104

    Article  Google Scholar 

  • Tan C, Ma B, Chen X (2009) Intuitionistic fuzzy geometric aggregation operator based on fuzzy measure for multi-criteria group decision making, In 2009 Sixth international conference on fuzzy systems and knowledge discovery, 4, 545–549

  • Wang Z, Wang Y (2020) Prospect theory-based group decision-making with stochastic uncertainty and 2-tuple aspirations under linguistic assessments. Inform Fusion 56:81–92

    Article  Google Scholar 

  • Wan S (2013) Power average operators of trapezoidal intuitionistic fuzzy numbers and application to multi-attribute group decision making. Appl Math Model 37(6):4112–4126

    Article  MathSciNet  Google Scholar 

  • Wan S, Wang Q, Dong J (2013) The extended VIKOR method for multi-attribute group decision making with triangular intuitionistic fuzzy numbers. Knowl-Based Syst 52:65–77

    Article  Google Scholar 

  • Xu Z (2007) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15(6):1179–1187

    Article  Google Scholar 

  • Xu Z, Yager R (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J General Syst 35(4):417–433

    Article  MathSciNet  Google Scholar 

  • Xia M, Xu Z, Chen N (2011) Induced aggregation under confidence levels. Int J Uncertain Fuzziness Knowl-Based Syst 19(2):201–227

    Article  MathSciNet  Google Scholar 

  • Xia M, Xu Z, Zhu B (2012) Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl-Based Syst 31:78–88

    Article  Google Scholar 

  • Yager R (2013) Pythagorean fuzzy subsets, 2013 Joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), 57–61

  • Yager R (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965

    Article  Google Scholar 

  • Yager R (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Article  Google Scholar 

  • Yu D (2014) Intuitionistic fuzzy information aggregation under confidence levels. Appl Soft Comput 19:147–160

    Article  Google Scholar 

  • Zadeh L (1965) Fuzzy sets. Inform Technol Control 8(3):338–353

    Article  Google Scholar 

  • Zhan J, Malik H, Akram M (2019) Novel decision-making algoritheorems based on intuitionistic fuzzy rough environment. Int J Mach Learn Cybern 10(6):1459–1485

    Article  Google Scholar 

  • Zhan J, Sun B (2018) Covering-based intuitionistic fuzzy rough sets and applications in multi-attribute decision-making, Artif Intell Rev, 1–31. https://doi.org/10.1007/s10462-018-9674-7

  • Zhang K, Zhan J, Wu W, On multi-criteria decision-making method based on a fuzzy rough set model with fuzzy \(\alpha \)-neighborhoods, IEEE Trans Fuzzy Syst, https://doi.org/10.1109/TFUZZ.2020.3001670

  • Zhou W, Xu Z, Chen M (2015) Preference relations based on hesitant-intuitionistic fuzzy information and their application in group decision making. Comput Industrial Eng 87:163–175

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by National Key Research and Development Program of China (2019QY(Y)0301, the National Natural Science Foundation of China under Grant Nos. 12061067, 62176033 and 61936001, and the Natural Science Foundation of Chongqing No. cstc2019jcyj-cxttX0002.

Funding

No Funding is provided for preparation of the manuscript.

Author information

Authors and Affiliations

  1. School of Science, Chongqing University of Posts and Telecommunications, Chongqing, 400065, People’s Republic of China

    Yabin Shao & Ning Wang

  2. College of Mathematics and Statistics, Northwest Normal University, Lanzhou, 730070, People’s Republic of China

    Zengtai Gong

Authors
  1. Yabin Shao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ning Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Zengtai Gong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yabin Shao.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shao, Y., Wang, N. & Gong, Z. Multicriteria q-Rung orthopair fuzzy decision analysis: a novel approach based on Archimedean aggregation operators with the confidence levels. Soft Comput 26, 4375–4394 (2022). https://doi.org/10.1007/s00500-022-06776-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-06776-8

Keywords