An approach to construct entropies on interval-valued intuitionistic fuzzy sets by their distance functions | Soft Computing Skip to main content
Springer Nature Link
Log in

An approach to construct entropies on interval-valued intuitionistic fuzzy sets by their distance functions

  • Foundations
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

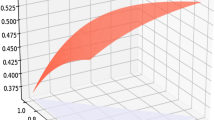
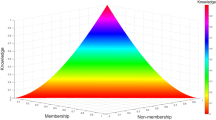
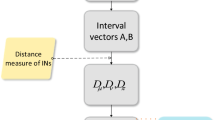
The main contribution of this paper is to give a new axiomatic definition of entropy measure and provide a constructing approach in the context of interval-valued intuitionistic fuzzy set (IVIFS). We give a new idea to define entropy on IVIFS: From the graphical representation, we consider the difference between a given IVIFS and its corresponding two interval fuzzy sets (IVFSs) by introducing a distance function that meets some specific conditions. The relationship between the distance function and the distance measure has also been illustrated. Based on distance functions, we give an approach to construct entropy measures on IVIFS. Then, a plenty of new entropies on IVIFS are introduced. Furthermore, we use a comparative example to show the proposed measures outperform the existing measures and utilize a demonstrative example to explain the application of the entropy measure in the multi-criteria decision making (MCDM), which verify the feasibility of our entropy construction method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    Article  Google Scholar 

  • Atanassov KT, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349

    Article  MathSciNet  Google Scholar 

  • Burillo P, Bustince H (1996) Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst 78(3):305–316

    Article  MathSciNet  Google Scholar 

  • Bustince H, Marco-Detchart C, Fernandez J, Wagner C, Garibaldi J, Takac Z (2019) Similarity between interval-valued fuzzy sets taking into account the width of the intervals and admissible orders. Fuzzy Sets Syst 390:23–47

    Article  MathSciNet  Google Scholar 

  • Chen T (2013) An interval-valued intuitionistic fuzzy linmap method with inclusion comparison possibilities and hybrid averaging operations for multiple criteria group decision making. Knowl Based Syst 45:134–146

    Article  Google Scholar 

  • Das S, Dutta B, Guha D (2016) Weight computation of criteria in a decision-making problem by knowledge measure with intuitionistic fuzzy set and interval-valued intuitionistic fuzzy set. Soft Comput 20(9):3421–3442

    Article  Google Scholar 

  • De Miguel L, Bustince H, Fernandez J, Indurain E, Kolesarova A, Mesiar R (2016) Construction of admissible linear orders for interval-valued atanassov intuitionistic fuzzy sets with an application to decision making. Inf Fus 27:189–197

    Article  Google Scholar 

  • Deng Y (2020) Uncertainty measure in evidence theory. Sci China Inf Sci 63:210201

    Article  MathSciNet  Google Scholar 

  • Düğenci M (2016) A new distance measure for interval valued intuitionistic fuzzy sets and its application to group decision making problems with incomplete weights information. Appl Soft Comput 41:120–134

    Article  Google Scholar 

  • Hung W, Yang M (2006) Fuzzy entropy on intuitionistic fuzzy sets. Int J Intell Syst 21(4):443–451

    Article  Google Scholar 

  • Jin F, Pei L, Chen H, Zhou L (2014) Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making. Knowl Based Syst 59:132–141

    Article  Google Scholar 

  • Li D (2010) Linear programming method for madm with interval-valued intuitionistic fuzzy sets. Expert Syst Appl 37(8):5939–5945

    Article  Google Scholar 

  • Li Y, Pelusi D, Deng Y (2020) Generate two-dimensional belief function based on an improved similarity measure of trapezoidal fuzzy numbers. Comput Appl Math 39:326

    Article  MathSciNet  Google Scholar 

  • Liu X, Zheng S, Xiong F (2005) Entropy and subsethood for general interval-valued intuitionistic fuzzy sets. In: International conference on fuzzy systems and knowledge discovery. pp 42–52

  • Liu Y, Jiang W (2020) A new distance measure of interval-valued intuitionistic fuzzy sets and its application in decision making. Soft Comput 24(9):6987–7003

    Article  Google Scholar 

  • Montes I, Pal NR, Montes S (2018) Entropy measures for atanassov intuitionistic fuzzy sets based on divergence. Soft Comput 22(15):5051–5071

    Article  Google Scholar 

  • Nguyen H (2016) A new interval-valued knowledge measure for interval-valued intuitionistic fuzzy sets and application in decision making. Expert Syst Appl 56:143–155

    Article  Google Scholar 

  • Park DG, Kwun YC, Park JH, Park IY (2009) Correlation coefficient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision making problems. Math Comput Modell 50(9–10):1279–1293

    Article  MathSciNet  Google Scholar 

  • Suo C, Li Y, Li Z (2021a) A series of information measures of hesitant fuzzy soft sets and their application in decision making. Soft Comput 25(6):4771–4784

    Article  Google Scholar 

  • Suo C, Yongming L, Zhihui L (2021b) On \(n\)-polygonal interval-value fuzzy sets and numbers. Fuzzy Sets Syst. https://doi.org/10.1016/j.fss.2020.10.014

  • Szmidt E, Kacprzyk J (2001) Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst 118(3):467–477

    Article  MathSciNet  Google Scholar 

  • Vlachos IK, Sergiadis GD (2006) Inner product based entropy in the intuitionistic fuzzy setting. Int J Uncertain Fuzziness Knowl Based Syst 14(03):351–366

    Article  MathSciNet  Google Scholar 

  • Vlachos IK, Sergiadis GD (2007) Intuitionistic fuzzy information-applications to pattern recognition. Pattern Recognit Lett 28(2):197–206

    Article  Google Scholar 

  • Wei C, Wang P, Zhang Y (2011) Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf Sci 181(19):4273–4286

    Article  MathSciNet  Google Scholar 

  • Wei C, Zhang Y (2015) Entropy measures for interval-valued intuitionistic fuzzy sets and their application in group decision-making. Math Probl Eng, pp 1–13

  • Xia M, Xu Z (2012) Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf Fus 13(1):31–47

    Article  Google Scholar 

  • Xu Z (2007) Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis 22(2):215–219

    Google Scholar 

  • Xue Y, Deng Y, Garg H (2020) Uncertain database retrieval with measure-based belief function attribute values under intuitionistic fuzzy set. Inf Sci 546:436–447

    Article  MathSciNet  Google Scholar 

  • Ye J (2010a) Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets. Appl Math Modell 34(12):3864–3870

    Article  MathSciNet  Google Scholar 

  • Ye J (2010b) Two effective measures of intuitionistic fuzzy entropy. Computing 87(1–2):55–62

    Article  MathSciNet  Google Scholar 

  • Ye J (2013) Interval-valued intuitionistic fuzzy cosine similarity measures for multiple attribute decision-making. Int J Gen Syst 42(8):883–891

    Article  MathSciNet  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    Article  Google Scholar 

  • Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning-1. Inf Sci 8(1):199–249

    Article  MathSciNet  Google Scholar 

  • Zeng W, Li H (2006) Relationship between similarity measure and entropy of interval valued fuzzy sets. Fuzzy Sets Syst 157(11):1477–1484

    Article  MathSciNet  Google Scholar 

  • Zhang H, Zhang W, Mei C (2009) Entropy of interval-valued fuzzy sets based on distance and its relationship with similarity measure. Knowl Based Syst 22(6):449–454

    Article  Google Scholar 

  • Zhang Q, Jiang S (2010) Relationships between entropy and similarity measure of interval-valued intuitionistic fuzzy sets. Int J Intell Syst 25(11):1121–1140

    MATH  Google Scholar 

  • Zhang Q, Jiang S, Jia B, Luo S (2010) Some information measures for interval-valued intuitionistic fuzzy sets. Inf Sci 180(24):5130–5145

    Article  MathSciNet  Google Scholar 

  • Zhang Q, Xing H, Liu F, Ye J, Tang P (2014) Some new entropy measures for interval-valued intuitionistic fuzzy sets based on distances and their relationships with similarity and inclusion measures. Inf Sci 283:55–69

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for helping them refine the ideas presented in this paper and improve the clarity of the presentation. This paper was supported by National Science Foundation of China (Grant Nos.: 11671244, 12071271) and the Higher School Doctoral Subject Foundation of Ministry of Education of China (Grant No.: 20130202110001).

Author information

Authors and Affiliations

  1. College of Mathematics and Information Science, Shaanxi Normal University, Xi’an, 710062, Shaanxi, People’s Republic of China

    Renqing Che, Chunfeng Suo & Yongming Li

Authors
  1. Renqing Che
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chunfeng Suo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yongming Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

RC and CS contributed to study conception and design. RC and YL contributed to analysis and interpretation of data. RC and CS contributed to programming. RC, CS and YL contributed to drafting of manuscript. RC, CS and YL contributed to critical revision.

Corresponding author

Correspondence to Yongming Li.

Ethics declarations

Conflict of interest

All authors agree to contribute without conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Che, R., Suo, C. & Li, Y. An approach to construct entropies on interval-valued intuitionistic fuzzy sets by their distance functions. Soft Comput 25, 6879–6889 (2021). https://doi.org/10.1007/s00500-021-05713-5

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-021-05713-5

Keywords