Local multigranulation decision-theoretic rough set in ordered information systems | Soft Computing Skip to main content
Springer Nature Link
Log in

Local multigranulation decision-theoretic rough set in ordered information systems

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

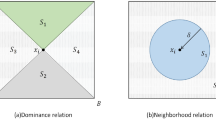
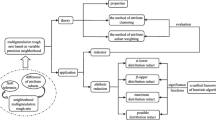
As a generalized extension of Pawlak’s rough set model, the multigranulation decision-theoretic rough set model in ordered information systems utilizes the basic set assignment function to construct probability measure spaces through dominance relations. It is an effective tool to deal with uncertain problems and widely used in practical decision problems. However, when the scale of dataset is large, it takes a lot of time to characterize the approximations of the target concept, as well as complicated calculation processes. In this paper, we develop a novel model called local multigranulation decision-theoretic rough set in an ordered information system to overcome the above-mentioned limitation. Firstly, to reduce the computing time of the information granule independent of the target concept, we only use the characterization of the elements in the target concept to approximate this target concept. Moreover, the corresponding local multigranulation decision-theoretic rough set in an ordered information system is addressed according to the established local model, and the comparisons are made between the proposed local algorithm and the algorithm of original multigranulation decision-theoretic rough set in ordered information systems. Finally, the validity of the local approximation operators is verified through the experimental evaluation using six datasets coming from the University of California-Irvine (UCI) repository.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Bansal S (2018) Nature-inspired-based multi-objective hybrid algorithms to find near-OGRs for optical WDM systems and their comparison. In: Handbook of research on biomimicry in information retrieval and knowledge management. IGI Global, pp 175–211

  • Bansal S, Gupta N, Singh AK (2017) NatureCinspired metaheuristic algorithms to find nearCOGR sequences for WDM channel allocation and their performance comparison. Open Math 15(1):520–547

    Article  MathSciNet  MATH  Google Scholar 

  • Bansal S, Singh AK, Gupta N (2017) Optimal golomb ruler sequences generation for optical WDM systems: a novel parallel hybrid multi-objective bat algorithm. J Inst Eng 98(1):43–64

    Google Scholar 

  • Bansal S, Sharma K (2018) Nature-inspired-based modified multi-objective BB-BC algorithm to find near-OGRs for optical WDM systems and its performance comparison. In: Handbook of research on biomimicry in information retrieval and knowledge management. IGI Global, pp 1–25

  • Chen J, Zhang YP, Zhao S (2016) Multi-granular mining for boundary regions in three-way decision theory. Knowl Based Syst 91:287–292

    Article  Google Scholar 

  • Du WS, Hu BQ (2016) Dominance-based rough set approach to incomplete ordered information systems. Inf Sci 346–347:106–129

    Article  MathSciNet  MATH  Google Scholar 

  • Du WS, Hu BQ (2017) Dominance-based rough fuzzy set approach and its application to rule induction. Eur J Oper Res 261(2):690–703

    Article  MathSciNet  MATH  Google Scholar 

  • Duntsh I, Gediga G (1998) Uncertainty measures of rough set prediction. Artif Intell 106(1):109–137

    Article  MathSciNet  MATH  Google Scholar 

  • Fang Y, Min F (2019) Cost-sensitive approximate attribute reduction with three-way decisions. Int J Approx Reason 104:148–165

    Article  MathSciNet  MATH  Google Scholar 

  • Greco S, Matarazzo B, Slowinski R (2002) Rough approximation by dominance relations. Int J Intell Syst 17(2):153–171

    Article  MATH  Google Scholar 

  • Greco S, Slwìski R, Yao YY (2007) Bayesian decision theory for dominance-based rough set approach. Rough Sets Knowl Technol 4481:134–141

    Article  Google Scholar 

  • Hu XH, Cercone N (1995) Learning in relational databases: a rough set approach. Comput Intell 11(2):323–338

    Article  Google Scholar 

  • Jeon G, Kim D, Jeong J (2016) Rough sets attributes reduction based expert system in interlaced video sequences. IEEE Trans Consum Electron 52(4):1348–1355

    Article  Google Scholar 

  • Li SY, Li TR (2015) Incremental update of approximations in dominance-based rough sets approach under the variation of attribute values. Inf Sci 294:348–361

    Article  MathSciNet  MATH  Google Scholar 

  • Li WT, Xu WH (2015) Multigranulation decision-theoretic rough set in ordered information system. Fundam Inform 139(1):67–89

    Article  MathSciNet  MATH  Google Scholar 

  • Li HX, Zhang LB, Huang B, Zhou XZ (2016) Sequential three-way decision and granulation for cost-sensitive face recognition. Knowl Based Syst 91:241–251

    Article  Google Scholar 

  • Li WT, Pedrycz W, Xue XP, Xu WH, Fan BJ (2018) Distance-based double-quantitative rough fuzzy sets with logic operations. Int J Approx Reason 101:206–233

    Article  MathSciNet  MATH  Google Scholar 

  • Li WT, Pedrycz W, Xue XP et al (2018) Fuzziness and incremental information of disjoint regions in double-quantitative decision-theoretic rough set model. Int J Mach Learn Cybern. https://doi.org/10.1007/s13042-018-0893-7

    Article  Google Scholar 

  • Liang DC, Pedrycz W, Liu D, Hu P (2015) Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making. Appl Soft Comput 29:256–269

    Article  Google Scholar 

  • Liang DC, Liu D, Kobina A (2016) Three-way group decisions with decision-theoretic rough sets. Inf Sci 345(1):46–64

    Article  Google Scholar 

  • Li W, Miao DQ, Wang WL et al (2010) Hierarchical rough decision theoretic framework for text classification. In: IEEE international conference on cognitive informatics, pp 484–489

  • Liu D, Yao YY, Li TR (2011) Three-way investment decisions with decision-theoretic rough sets. Int J Comput Intell Syst 4(1):66–74

    Article  Google Scholar 

  • Liu D, Li TR, Liang DC (2012) Three-way government decision analysis with decision-theoretic rough sets. Int J Uncertain Fuzziness Knowl Based Syst 20(supp01):119–132

    Article  Google Scholar 

  • Ma WM, Sun BZ (2012) Probabilistic rough set over two universes and rough entropy. Int J Approx Reason 539(4):608–619

    Article  MathSciNet  MATH  Google Scholar 

  • Pawlak Z (1982) Rough set. Int J Comput Inf Sci 11(5):341–356

    Article  MATH  Google Scholar 

  • Pawlak Z (1992) Rough sets: theoretical aspects of reasoning about data. Kluwer Academic Publishers, Alphen ann den Rijn

    MATH  Google Scholar 

  • Pawlak Z, Wong SKM, Ziarko W (1988) Rough sets: probabilistic versus deterministic approach. Int J Man Mach Stud 29(1):81–95

    Article  MATH  Google Scholar 

  • Pedrycz W (2013) Granular computing: analysis and design of intelligent systems. CRC Press, Boca Raton

    Book  Google Scholar 

  • Qian YH, Liang JY (2006) Rough set method based on multi-Granulations. IEEE Int Conf Cognit Inform 1:297–304

    Google Scholar 

  • Qian YH, Zhang H, Sang YL et al (2014) Multigranulation decision-theoretic rough sets. Int J Approx Reason 55(1):225–237

    Article  MathSciNet  MATH  Google Scholar 

  • Qian YH, Li SY, Liang JY et al (2014) Pessimistic rough set based decisions: a multigranulation fusion strategy. Inf Sci 264:196–210

    Article  MathSciNet  MATH  Google Scholar 

  • Qian YH, Liang XY, Lin GP et al (2017) Local multigranulation decision-theoretic rough sets. Int J Approx Reason 82:119–137

    Article  MathSciNet  MATH  Google Scholar 

  • Qian J, Liu CH, Yue XD (2019) Multigranulation sequential three-way decisions based on multiple thresholds. Int J Approx Reason 105:396–416

    Article  MathSciNet  MATH  Google Scholar 

  • Shao MW, Zhang WX (2005) Dominance relation and rules in an incomplete ordered information system. Int J Intell Syst 20(1):13–27

    Article  MATH  Google Scholar 

  • Sun BZ, Ma WM, Li BJ, Li XN (2016) Three-way decisions approach to multiple attribute group decision making with linguistic information-based decision-theoretic rough fuzzy set. Int J Approx Reason 93:424–442

    Article  MathSciNet  MATH  Google Scholar 

  • Susmaga R (2014) Reducts and constructs in classic and dominance-based rough sets approach. Inf Sci 271:45–64

    Article  MathSciNet  MATH  Google Scholar 

  • Xu WH (2013) Ordered information systems and rough sets theory. Science Press, Beijing

    Google Scholar 

  • Xu WH, Li WT (2016) Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets. IEEE Trans Cybern 46(2):366–379

    Article  MathSciNet  Google Scholar 

  • Xu WH, Yu JH (2017) A novel approach to information fusion in multi-source datasets: a granular computing viewpoint. Inf Sci 378:410–423

    Article  Google Scholar 

  • Xu WH, Zhang XY, Zhong JM et al (2010) Attribute reduction in ordered information systems based on evidence theory. Knowl Inf Syst 25(1):169–184

    Article  Google Scholar 

  • Yao YY (1998) Generalized rough set models. Rough Sets Knowl Discov 1:286–318

    MathSciNet  MATH  Google Scholar 

  • Yao YY (2007) Decision-theoretic rough set models. Rough Sets Knowl Technol 4481:1–12

    Article  Google Scholar 

  • Yao YY (2008) Probabilistic rough set approximation. Int J Approx Reason 49(2):255–271

    Article  MATH  Google Scholar 

  • Yao YY (2009) Three-way decision: An interpretation of rules in rough set theory. Rough Sets Knowl Technol 5589:642–649

    Article  Google Scholar 

  • Yao YY, Wong SKM (1992) A decision theoretic framework for approximating concepts. Int J Man Mach Stud 37(6):793–809

    Article  Google Scholar 

  • Yao YY, Zhou B (2010) Naive Bayesian rough sets. Rough Sets Knowl Technol 6401:719–726

    Google Scholar 

  • Yu JH, Xu WH (2017) Incremental knowledge discovering in interval-valued decision information system with the dynamic data. Int J Mach Learn Cybern 8(1):849–864

    Article  Google Scholar 

  • Yu H, Liu ZG, Wang GY (2014) An automatic method to determine the number of clusters using decision-theoretic rough set. Int J Approx Reason 55(1):101–115

    Article  MathSciNet  MATH  Google Scholar 

  • Yu JH, Zhang B, Chen MH, Xu WH (2018) Double-quantitative decision-theoretic approach to multigranulation approximate space. Int J Approx Reason 98:236–258

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang XY, Miao DQ (2017) Three-way attribute reducts. Int J Approx Reason 88:401–434

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang HY, Leung Y, Zhou L (2013) Variable-precision-dominance-based rough set approach to interval-valued information systems. Inf Sci 244:75–91

    Article  MathSciNet  MATH  Google Scholar 

  • Ziarko W (1993) Variable precision rough set model. J Comput Syst Sci 46(1):39–59

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to express our thanks to the Editor-in-Chief, handling associate editor and anonymous referees for his/her valuable comments and constructive suggestions. This work is supported by the National Natural Science Foundation of China (No. 61772002).

Author information

Authors and Affiliations

  1. School of Sciences, Chongqing University of Technology, Chongqing, 400054, People’s Republic of China

    Jia Zhang

  2. School of Mathematics and Statistics, Southwest University, Chongqing, 400715, People’s Republic of China

    Xiaoyan Zhang & Weihua Xu

  3. School of Computer Science, Southwest Petroleum University, Chengdu, 610500, People’s Republic of China

    Yanxue Wu

Authors
  1. Jia Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoyan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weihua Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yanxue Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaoyan Zhang.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Communicated by V. Loia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Zhang, X., Xu, W. et al. Local multigranulation decision-theoretic rough set in ordered information systems . Soft Comput 23, 13247–13261 (2019). https://doi.org/10.1007/s00500-019-03868-w

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-019-03868-w

Keywords

Search

Navigation