Euclidean TSP in Narrow Strips

Abstract

We investigate how the complexity of Euclidean TSP for point sets P inside the strip $(-\infty ,+\infty )\times [0,\delta ]$ depends on the strip width $\delta$. We obtain two main results.

• For the case where the points have distinct integer x-coordinates, we prove that a shortest bitonic tour (which can be computed in $O(n\log ^2 n)$ time using an existing algorithm) is guaranteed to be a shortest tour overall when $\delta \leqslant 2\sqrt{2}$, a bound which is best possible.

• We present an algorithm that is fixed-parameter tractable with respect to $\delta$. Our algorithm has running time $2^{O(\sqrt{\delta })} n + O(\delta ^2 n^2)$ for sparse point sets, where each $1\times \delta$ rectangle inside the strip contains O(1) points. For random point sets, where the points are chosen uniformly at random from the rectangle $[0,n]\times [0,\delta ]$, it has an expected running time of $2^{O(\sqrt{\delta })} n$. These results generalise to point sets P inside a hypercylinder of width $\delta$. In this case, the factors $2^{O(\sqrt{\delta })}$ become $2^{O(\delta ^{1-1/d})}$.

Appendices

Appendix A: The Automated Prover

Algorithm 5

FindShorterTour$(n_\textrm{left},n_\textrm{right},\overline{F},\widetilde{E},X,\delta ,\varepsilon )$

Here, we will give an overview of the inner workings of the automated prover. See Algorithm 5 for pseudocode, which we will now explain. First, all candidate sets of edges $\overline{F}'$ that form a tour together with $\widetilde{E}$ are generated. Then, a set of cases is generated. Each case consists of the following:

• The x-coordinates of each of the points, stored in $\mathcal {X}$. Every point must have a different integer x-coordinate, and must adhere to the given bounds on the x-coordinates.

• For every point, an interval denoting the range in which its y-coordinate must lie, stored in $\mathcal {Y}$. When the cases are first generated, this is simply $[0,\delta ]$ for every point.

For each possible combination $\mathcal {X}$ of x-coordinates of the points, one such case is generated. Note that every possible set of points in represented by one of these cases. Then, for every case, it does the following:

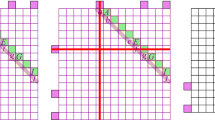
• To prove a case, it calculates an upper bound on the total lengths of every candidate $\overline{F}'$, and a lower bound of the total length of $\overline{F}$. For every edge, a lower bound can be found by simply taking the points as close together as possible, and an upper bound is found by doing the opposite. See Fig. 21 for some examples. Suppose there exists a set $\overline{F}'$ such that the upper bound on its length is guaranteed to be lower than the lower bound on the length of $\overline{F}$. Then $\Vert \overline{F}'\Vert < \Vert \overline{F}\Vert$ must hold, and the case holds. To counter rounding errors, the calculated upper bound must be more than some fixed $\eta :=10^{-6}$ lower than the calculated lower bound for this to trigger. The prover has been implemented in Java using doubles, which have a precision of up to 15 to 16 decimal digits.

• If it fails to prove the case, it splits the case into $2^{n_\textrm{left}+ n_\textrm{right}}$ cases, by splitting the interval of every y-coordinate into two equal parts. For example, if a case has two points and intervals [0, 2] and [6, 8], it is split into the four cases ([0, 1], [6, 7]), ([0, 1], [7, 8]), ([1, 2], [6, 7]) and ([1, 2], [7, 8]). Then, it recursively tries to prove all of these cases. If, however, the intervals become too small (smaller than the given precision parameter $\varepsilon$), the prover gives up on proving this case.

This process continues until all cases have been either proven or given up on. Finally, the prover returns a list of all cases and whether it succeeded or failed on these cases. Note that the smaller the precision parameter $\varepsilon$ is, the more precise the cases (and therefore the answer) will be. However, a smaller $\varepsilon$ will also result in more cases, which increases both the running time and the number of lines of the output.

Fig. 21

Three pairs of intervals, the shortest edges between points in those intervals (solid) and the longest edges between points in those intervals (dashed)

Appendix B: Omitted Proofs

1.1 Proof of Observation 6.2

See Fig. 22 for an example. Note that $x_{st^+\hspace{-1.111pt}(i)}$ is the x-coordinate of the rightmost point to the left of $t^+_i$, and that $x_{st^+\hspace{-1.111pt}(i)+1}$ is the x-coordinate of the leftmost point to the right of $t^+_i$. Therefore, $x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} > \delta / (2k)$.

Fig. 22

An example of Observation 6.2. Edges of T are shown in black, edges of $T'$ are shown in red

W.l.o.g., T contains the directed edge from $r_1$ to $r_2$. Suppose for a contradiction that T is an optimal tour and not bitonic at $t^+_i$. Then T must cross $t^+_i$ at least four times, which implies that there must be another directed edge $q_1 q_2$ with $x(q_1) \leqslant x_{st^+\hspace{-1.111pt}(i)}$ and $x_{st^+\hspace{-1.111pt}(i)+1} \leqslant x(q_2)$.

Note that $q_1 \ne r_1$ and $q_2 \ne r_2$, since a single point cannot have two incoming or two outgoing edges. We will now show that $| r_1 q_1| + |r_2 q_2| < |q_1 q_2| + |r_1 r_2|$. By Observation 3.1, we then get an optimal tour $T'$ shorter than T, thereby finishing the proof. First, we will simplify the problem using an argument similar to the proof of Observation 3.2. Suppose we move $q_1$ towards $q_2$ until $x(q_1) = x_{st^+\hspace{-1.111pt}(i)}$. By doing so, $|q_1 r_1|$ will never decrease more than $|q_1 q_2|$. Therefore, it is sufficient to prove the statement for $x(q_1) = x_{st^+\hspace{-1.111pt}(i)}$. Analogously, it is sufficient to prove the statement for $x(q_2) = x_{st^+\hspace{-1.111pt}(i)+1}$ and $x(r_1) + 2k \delta = x(q_1)$ and $x(q_2) + 2k \delta = x(r_2)$. Finally, recall that $x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} > \delta / (2k)$, so we will prove the statement for $x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} = \delta / (2k)$. Together, we now have

$$x(r_1) + 2k\delta = x(q_1) = x(q_2)-\delta /(2k) = x(r_2)-\delta /(2k)-2k\delta .$$

We get

$$\begin{aligned} |q_1 r_1| + |q_2 r_2|&\leqslant \sqrt{(x(q_1)-x(r_1))^2+\delta ^2} + \sqrt{(x(r_2)-x(q_2))^2+\delta ^2} \\&= 2 \delta \sqrt{ (2k)^2 + 1} \\&< 2 \delta (2k + 1/(2k))\\&= \delta /(2k) + (2 (2k\delta ) + \delta /(2k)) \\&= (x(q_2)-x(q_1)) + (x(r_2)-x(r_1)) \\&\leqslant |q_1 q_2| + |r_1 r_2|. \end{aligned}$$

By Observation 3.1, this gives us an optimal tour $T'$ shorter than T, thereby finishing the proof.