Abstract
We study the Minkowski length L(P) of a lattice polytope P, which is defined to be the largest number of non-trivial primitive segments whose Minkowski sum lies in P. The Minkowski length represents the largest possible number of factors in a factorization of polynomials with exponent vectors in P, and shows up in lower bounds for the minimum distance of toric codes. In this paper we give a polytime algorithm for computing L(P) where P is a 3D lattice polytope.
We next study 3D lattice polytopes of Minkowski length 1. In particular, we show that if Q, a subpolytope of P, is the Minkowski sum of L=L(P) lattice polytopes Q i , each of Minkowski length 1, then the total number of interior lattice points of the polytopes Q 1,…,Q L is at most 4. Both results extend previously known results for lattice polygons. Our methods differ substantially from those used in the two-dimensional case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let P be a convex lattice polytope in ℝn. Then P defines \(\mathcal{L}_{\mathbb {F}}(P)\), a vector space over a field \(\mathbb {F}\) spanned by the monomials in P. That is,
where \(t^{m}=t_{1}^{m_{1}}\cdots t_{n}^{m_{n}}\). In this paper we address the following question: What is the largest number of factors that a polynomial in \(\mathcal{L}_{\mathbb {F}}(P)\) could have? We also study those factors and obtain results regarding their Newton polytopes. Although these questions are interesting on its own, our motivation comes from studying toric codes.
The toric code \(\mathcal{C}_{P}\), first introduced by Hansen in [3], is defined by evaluating the polynomials in \(\mathcal {L}_{\mathbb {F}_{q}}(P)\) at all the points t in the algebraic torus \((\mathbb {F}_{q}^{*})^{n}\). That is, \(\mathcal{C}_{P}\) is a linear code whose codewords are the strings \((f(t)\ |\ t\in(\mathbb {F}_{q}^{*})^{n})\) for \(f\in\mathcal{L}_{\mathbb {F}_{q}}(P)\). It is convenient to assume that P is contained in the square [0,q−2]n, so that all the monomials in \(\mathcal{L}_{\mathbb {F}_{q}}(P)\) are linearly independent over \(\mathbb {F}_{q}\) [8]. Thus \(\mathcal{C}_{P}\) has block length (q−1)n and dimension equal to the number of the lattice points in P.
Note that the weight of each non-zero codeword in \(\mathcal{C}_{P}\) is the number of points \(t\in(\mathbb {F}_{q}^{*})^{n}\) where the corresponding polynomial does not vanish. Therefore, the minimum distance of \(\mathcal{C}_{P}\) (which is the minimum weight for linear codes) equals
where Z(f) is the number of zeroes (i.e. points of vanishing) in \((\mathbb {F}_{q}^{*})^{n}\) of f.
For toric surface codes, that is, in the case n=2, Little and Schenck in [6] used Hasse–Weyl bound and the intersection theory on toric surfaces to come up with the following general idea: If q is sufficiently large, then polynomials \(f\in\mathcal{L}_{\mathbb {F}_{q}}(P)\) with more absolutely irreducible factors will necessarily have more zeroes in \((\mathbb {F}_{q}^{*})^{2}\) ([6], Proposition 5.2). In [10] this idea was expanded to produce explicit bounds for the minimum distance of \(\mathcal{C}_{P}\) in terms of a certain geometric invariant L(P), (full) Minkowski length of P, which was introduced in that paper.
This invariant L(P) reflects the largest possible number of absolutely irreducible factors a polynomial \(f\in\mathcal{L}_{\mathbb {F}_{q}}(P)\) can have. A polytime algorithm for computing L(P) for polygons was provided in [10]. In this paper, we extend this result to dimension 3 (Theorem 3.7, based on Theorem 3.5).
Moreover, [10] provides a description of the factorization f=f 1⋯f L(P) for \(f\in\mathcal{L}_{\mathbb {F}_{q}}(P)\) with the largest number of factors: it turns out that in such a factorization the Newton polygon \(P_{f_{i}}\) (which is the convex hull of the exponents of the monomials in f i ) is either a primitive segment, a unit simplex, or a triangle with exactly one interior point. It is also shown in [10] that a triangle with an interior point can occur in such a factorization at most once. This implies that the total number I of interior lattice points of \(P_{f_{i}}\) is at most 1. This result is essential for establishing bounds on the minimum distance of toric surface codes in [10].
This argument is not directly extendable to dimension 3, as it does not seem feasible to obtain a description of the Newton polytopes \(P_{f_{i}}\) in dimension 3 (see [11] for some examples). Nevertheless, in this paper we show that in the 3D case I≤4 (Theorem 4.14). Our methods differ substantially from those used in the two-dimensional case. An initial version of our argument relied heavily on the classification of 3D Fano tetrahedra [4]. Although we were able to completely get rid of this dependency in our final argument, the classification helped us significantly in our explorations.
In [10] combinatorial results about Minkowski length of polygons lead to lower bounds on the minimum distance of surface toric codes. We hope that our (entirely combinatorial) paper will in the future lead to similar bounds for 3D toric codes.
2 Minkowski Length of Lattice Polytopes
Here we recall the definition of the (full) Minkowski length introduced in [10] as well as reproduce and refine some results from that paper using new methods which will later be applied to the 3D case.
2.1 Minkowski Sum
Let P and Q be convex polytopes in ℝn. Their Minkowski sum is
which is again a convex polytope. Figure 1 shows the Minkowski sum of a triangle and a square.
Let f be a Laurent polynomial in \(\mathbb {F}_{q}[t_{1}^{\pm1},\dots,t_{n}^{\pm 1}]\). Then its Newton polytope P f is the convex hull of the exponent vectors of the monomials appearing in f. Thus P f is a lattice polytope as its vertices belong to the integer lattice ℤn⊂ℝn. Note that if \(f,g\in \mathbb {F}_{q}[t_{1}^{\pm1},\dots,t_{n}^{\pm1}]\) then the Newton polytope of their product P fg is the Minkowski sum P f +P g . A primitive segment E is a lattice segment whose only lattice points are its endpoints. The difference of the endpoints is a vector v E whose coordinates are relatively prime (v E is defined up to sign). A polytope which is the Minkowski sum of primitive segments is called a (lattice) zonotope. We say that two lattice polytopes are equal if they are the same up to translation.
The automorphism group of the lattice is the group of affine unimodular transformations, denoted by \(\operatorname {AGL}(n,\mathbb {Z})\), which consists of translations by an integer vector and linear transformations in \(\operatorname {GL}(n,\mathbb {Z})\). It is a standard fact from lattice-point geometry that any two primitive segments in ℝn are \(\operatorname {AGL}(n,\mathbb {Z})\)-equivalent ([7], Theorem II.1).
2.2 Minkowski Length
Let P be a lattice polytope in ℝn.
Definition 2.1
The (full) Minkowski length L=L(P) of a lattice polytope P is the largest number of primitive segments E 1,E 2,…,E L whose Minkowski sum is in P. Equivalently, L=L(P) is the largest number of non-trivial lattice polytopes Q 1,…,Q L whose Minkowski sum is in P. Any collection of L=L(P) non-trivial lattice polytopes Q 1,…,Q L whose Minkowski sum is in P will be referred to as a maximal (Minkowski) decomposition in P. The dimension of a maximal decomposition is the dimension of the Minkowski sum Q 1+⋯+Q L .
Example 2.2
In the figure below, the first polygon, called T 0, has Minkowski length 1. For the second one, the Minkowski length is 2. Notice that this triangle has many maximal decompositions: the sum of two horizontal segments, the sum of two vertical segments, the sum of two diagonal segments, the sum of two standard 2-simplices, etc. For the last polygon, the Minkowski length is 3, as there is a parallelogram inside that is a sum of three lattice segments.

Clearly, L(P) is an \(\operatorname {AGL}(n,\mathbb {Z})\)-invariant and the summands of every maximal decomposition in P are polytopes of Minkowski length 1.
It does not seem feasible to describe polytopes of Minkowski length 1 in general. However, in dimension 2 such a description is given in [10] and we reproduce it here.
Theorem 2.3
[10]
Let P be a convex lattice polygon in the plane with L(P)=1. Then P is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to a primitive segment, the standard 2-simplex \(\mathcal{D}\) or the triangle T 0 with vertices (1,0), (0,1), and (2,2), as shown in Fig. 2.
It is also proved in [10] that a maximal decomposition Q⊆P can have at most one summand \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to T 0, and if this is the case, the remaining summands are [0,e 1], [0,e 2], and [0,e 3], that is, Q is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to Q=T 0+n 1[0,e 1]+n 2[0,e 2]+n 3[0,e 1+e 2]. Here e 1,e 2 are the standard basis vectors.
We will recover this result (using a new method that will be later applied to the 3D case) and will also show that if a triangle Δ is a summand of a maximal decomposition of a polygon P, then the other summands are either primitive segments, or exactly that triangle Δ. That is, if Q 1 and Q 2 are triangles and L(Q 1+Q 2)=2, then Q 1=Q 2. This refinement will be important for our 3D discussion.
Before we state the result, we set notation and prove a lemma which will also be important for our future discussion in dimension 3. Let P be a lattice polytope in ℝn. For each segment whose endpoints are lattice points in P, consider its direction vector reduced modulo 3. Since v and −v define the same segment, we identify such vectors. Using this equivalence relation, we obtain the set ℤ3ℙn−1 of equivalence classes.
Lemma 2.4
Let L(P)=L(Q)=1 and L(P+Q)=2, where P and Q are lattice polytopes in ℝn. Then if P and Q each have a segment of some class a, then those two segments are equal (are the same up to translation). If P has at least two segments of class a, then Q has no segments from that class.
Proof
If P and Q both have lattice segments from the same equivalence class, then, unless these segments are equal, their Minkowski sum contains a segment of Minkowski length 3 (since either sum or difference of the direction vectors is a multiple of 3). If P has multiple segments from one class, then these segments cannot be translates of each other, as they would form a parallelogram in P of Minkowski length at least 2. If Q has a segment from that class, it would be not a translate of at least one of the two segments in P and we again conclude L(P+Q)≥3. □
Theorem 2.5
Let P be a convex lattice polygon. If one of the summands of a maximal decomposition Q in P is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to T 0, then Q is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to Q=T 0+n 1[0,e 1]+n 2[0,e 2]+n 3[0,e 1+e 2]. If one of the summands Δ of Q is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to the standard 2-simplex, then the remaining summands that are not primitive segments, are equal to Δ.
Proof
We have four equivalence classes in ℤ3ℙ1:
Notice that if a and b∈ℤ3ℙ1 are linearly independent (that is, a≠±b), then they generate all the classes:
Now let one of the summands in a maximal decomposition in P be \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to T 0. Then we can assume this summand is exactly T 0. The direction vectors of the lattice segments in T 0 are (1,0), (0,1), (1,1), (1,−1), (1,2), and (2,1). The last three are all from the same class, so by Lemma 2.4 segments from this class cannot show up in other summands. The first three are all from distinct classes, hence by the lemma only segments with direction vectors (1,0), (0,1), and (1,1) can show up in other summands. Since all four classes are covered, we have shown that the direction vectors of lattice segments in other summands can only be (1,0), (0,1), and (1,1). One can use such segments to form a triangle in four different ways. The result will be the standard 2-simplex and its reflections. In each of these four cases, it is easy to check that the Minkowski sum of such a triangle with T 0 is 3, which proves our first statement.
Next, let one of the summands be equivalent to the standard 2-simplex Δ, so we can assume it is exactly Δ. The direction vectors (1,0),(0,1), and (−1,1) are all from distinct classes, hence if other summands have lattice segments from these classes, they would have to have these direction vectors. If there is another triangle in the maximal decomposition, it would have to be equivalent to the standard 2-simplex, as T 0 is not possible by the above argument. The direction vectors would have to belong to three distinct classes, so at least two of the sides would have to have direction vectors (1,0),(0,1), or (−1,1). Here are eight triangles that could be formed in this way:

The last four have a segment with a direction vector either (−2,1) or (−1,2), which are from the same class with (1,1), so the Minkowski sum of any of these triangles with Δ is at least 3. For all the remaining triangles, except Δ itself we easily check that their sum with Δ has Minkowski length 3.

□
Corollary 2.6
Let P,Q be lattice polytopes in ℝ3 with L(P+Q)=2. Consider the intersection of a plane π with each P and Q. If each π∩P and π∩Q contains a lattice triangle, then these lattice triangles are the same up to translation.
Proof
Let u be a primitive normal vector to π. Let A∈GL(3,ℤ) be a matrix whose last row is u. (It is shown, for example, in [7], Theorem II.1, why such a matrix exists.) Then A maps π to the (x,y)-plane and the result follows from the previous theorem. □
3 Algorithm for Computing L(P) for 3D polytopes
It was shown in [10] that in the plane case there always exists a maximal decomposition in P of a very simple form. Namely, there exists a maximal decomposition that is equivalent to n 1[0,e 1]+n 2[0,e 2]+n 3[0,e 1+e 2] for some n 1,n 2,n 3∈ℕ. This fact was used in [10] to build an algorithm for finding L(P). To extend this result to the 3D case, we first make a definition.
Definition 3.1
Let P⊂ℝn be a convex lattice polytope. Then the set of its maximal decompositions is partially ordered by inclusion. That is, we say that
if A+P 1+⋯+P k ⊆̷B+Q 1+⋯+Q l . Here A and B are points in ℤn. A maximal decomposition is called a smallest maximal decomposition if it is minimal with respect to this partial order. Note that a smallest maximal decomposition is a Minkowski sum of segments.
Proposition 3.2
Let P⊆ℝ2 be a lattice polygon. Consider a smallest maximal decomposition Z in P:
Then Area(E i +E j )≤1 for any choice of 1≤i,j≤l.
Proof
Let v 1 and v 2 be the primitive direction vectors of the segments E i and E j and assume that the area of the parallelogram spanned by v 1 and v 2 is at least 2. Applying an \(\operatorname {AGL}(2,\mathbb {Z})\) transformation, we can assume that A is the origin, v 1=e 1=(1,0) and v 2=(a,b), where 0≤a<b and b>1, which implies that (1,1)∈Π=[0,e 1]+[0,(a,b)]. We show now that there is always a segment I of Minkowski length 2 that lies strictly inside Π and hence, we can pass from Π to 2I and get a smaller maximal decomposition. If both a and b are even then 2[0,(a/2,b/2)] is strictly inside of Π; if a is odd and b is even then 2[0,((a+1)/2,b/2)]⊆̷Π; if a is even and b is odd, (1,1)+2[0,(a/2,(b−1)/2)]⊆̷Π; if a and b are both odd, (1,1)+2[0,((a−1)/2),((b−1)/2)]⊆̷Π. □
Theorem 3.3
Let P⊆ℝ2 be a lattice polygon. If Z is a smallest maximal decomposition in P, then it is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to
Proof
Let P⊇Z=n 1 E 1+⋯+n l E l with v 1,…,v l distinct primitive direction vectors of the segments E 1,…,E l . Applying an \(\operatorname {AGL}(2,\mathbb {Z})\) transformation we can assume that v 1=e 1. Next, since det(v 1,v 2)=±1, we can assume that v 2=e 2. Then by the previous proposition, any other v k is either (1,1) or (1,−1) as we can always switch a vector to its negative. Notice that these two vectors cannot simultaneously appear in a smallest decomposition, as the sum of the corresponding segments would contain a segment of Minkowski length 2. Finally, these two remaining cases are \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent. □
We next treat the 3D case.
Proposition 3.4
Let P⊂ℝ3 be a lattice polytope. Consider a smallest maximal decomposition Z in P
Then Vol(E i +E j +E k )≤2 for any choice of 1≤i,j,k≤l.
Proof
Let v 1, v 2, and v 3 be the primitive vectors that go along the segments E i , E j , E k , and assume that the volume of the parallelepiped spanned by v 1, v 2, and v 3 is at least 3. Applying an \(\operatorname {AGL}(2,\mathbb {Z})\) transformation (and using Proposition 3.2), we can assume that A is the origin, v 1=e 1=(1,0,0), v 2=e 2=(0,1,0), and v 3=(s,t,u), where 0≤s≤t<u. The volume of the parallelepiped spanned by e 1,e 2,v 3 is |u|. If s=0, then the area spanned by e 2 and v 3 is |u|≥3, which would contradict the minimality of Z. We next observe that the parallelepiped spanned by e 1,e 2, and v 3 is defined by
and consider the following three cases.
-
Case 1.
s≤u/2, t≤u/2
Using the description of Π above, we can easily check that (1,1,2) and (s,t,u−2) are both in Π. Hence a parallelogram with the vertices (1,1,0),(1,1,2),(s,t,u−2), and (s,t,u) is inside Π. This parallelogram is a Minkowski sum of three segments
$$(1,1,0)+2\bigl[0,(0,0,1)\bigr]+\bigl[0,(s-1,t-1,u-2)\bigr]\subsetneq\varPi, $$which contradicts the minimality of Z. Notice that u≥3 ensures that the segments involved in the decomposition are non-trivial.
-
Case 2.
s>u/2, t>u/2
Then (2,2,2) and (s−1,t−1,u−2) are in Π, so a parallelogram with the vertices (0,0,0),(2,2,2),(s−1,t−1,u−2), and (s+1,t+1,u) is inside Π. This parallelogram is a Minkowski sum of three segments
$$2\bigl[0, (1,1,1)\bigr]+\bigl[0, (s-1,t-1,u-2)\bigr]\subsetneq\varPi, $$which contradicts the minimality of Z.
-
Case 3.
s≤u/2, t>u/2
Then (1,2,2) and (s,t−1,u−2) are in Π, so a parallelogram with the vertices (1,0,0),(1,2,2),(s,t−1,u−2), and (s,t+1,u) is inside Π. This parallelogram is a Minkowski sum of three segments
$$(1,0,0)+2\bigl[0, (0,1,1)\bigr]+\bigl[0, (s-1,t-1,u-2)\bigr]\subsetneq\varPi, $$and we get the same contradiction again.
□
Theorem 3.5
Let P⊂ℝ3 be a lattice polytope. Let Z be a smallest maximal decomposition in P, then it is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to either

or

Proof
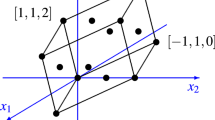
Assume first that there are three segments in the maximal decomposition Z whose direction vectors generate a parallelepiped of volume 2. We can then assume that the first direction vector is e 1. By Proposition 3.2 we can assume that the second vector is e 2. Next, we can assume that the third direction vector v is of the form (s,t,u) where 0≤s≤t<u. Since 2=|det(e 1,e 2,v)|, we know that u=2 and the only options for the third vector are (0,1,2) and (1,1,2). The first of these two options is impossible, as the sum of (0,1,2) and (0,1,0) is not primitive, which contradicts the minimality of Z. We have shown that the third vector is (1,1,2)=e 1+e 2+2e 3.
Let v=(a,b,c) be a direction vector of some other segment in the maximal decomposition Z. We know that |det(e 1,e 2,v)|≤2, |det(e 1,e 1+e 2+2e 3,v)|≤2, and |det(e 2,e 1+e 2+2e 3,v)|≤2, which gives us the following restraints on the components of v: |c−2b|≤2, |c−2a|≤2, and |c|≤2. By flipping the direction vector v if necessary, we can assume that c≥0.
If c=0, then v=(1,1,0) or (1,−1,0). Both options are impossible as then the sum of v with (1,1,2) is (2,2,2) or (2,2,0), so we can pass to a smaller maximal decomposition. If c=1, then v=(0,0,1), (0,1,1), (1,0,1), (1,1,1). If c=2, then v=(0,1,2), (1,0,2), (1,2,2), or (2,1,2). Adding either e 1 or e 2 to each of these four vectors we can get a non-primitive vector, so none of these vectors occur in our maximal decomposition. We have shown that in the case when there are three segments in the maximal decomposition Z that generate a parallelepiped of volume 2, then Z is \(\operatorname {AGL}(2,\mathbb {Z})\)-equivalent to

Next, assume that any three segments in the maximal decomposition Z generate a parallelepiped of volume at most 1. If for any three vectors the volume is zero, then we are in the plane case and we are done. Otherwise, we can assume that the first three vectors are e 1, e 2, and e 3. Let v=(a,b,c) be any other direction vector in the maximal decomposition Z. Then we have |a|≤1, |b|≤1 and |c|≤1. By flipping the direction vector we can assume that c≥0. Here are the options for v that we get, written in four lines:

Notice that no two vectors from the same line here can occur in Z together as their sum is not primitive, which would contradict the minimality of Z. By flipping the direction of basis vectors, we can assume that if any of the four vectors in the last line occur in Z, then it is (1,1,1). Let us assume that this is the case and (1,1,1) occurs in Z.
We notice next (−1,0,1) and (0,−1,1) cannot occur in Z together as if we add these two vectors together with (1,1,1), we get (0,0,3). We can make the same observation about (−1,0,1) and (1,−1,0) and then about (0,−1,1) and (1,−1,0). This implies that only one of (1,−1,0), (0,−1,1), and (−1,0,1) occurs in Z. By permuting e 1,e 2, and e 3 we can assume that the one that occurs is (1,−1,0).
In the case when none of the four vectors (1,1,1), (1,−1,1), (−1,1,1), (−1,−1,1) occur in Z, by applying a diagonal change of basis with ±1’s on the main diagonal (which will not change [0,e 1],[0,e 2], [0,e 3]), we can turn any pair of vectors from the set (1,−1,0),(0,−1,1),(−1,0,1) into corresponding vectors with positive entries. For example, a matrix with the diagonal entries −1,−1,1 will turn (−1,0,1) and (0,−1,1) into (1,0,1) and (0,1,1). Hence we will be able to get rid of all the vectors with negative entires except, possibly, one. By permuting e 1, e 2, and e 3, we can assume that the vector with a negative entry is (1,−1,0). We have shown that if any three segments in Z generate a parallelepiped of volume at most 1, then Z is \(\operatorname {AGL}(3,\mathbb {Z})\)-equivalent to either

or

□
Notice that in 2D a smallest maximal decomposition has at most three distinct summands; in 3D, as we have just shown, such a decomposition has at most seven distinct summands. It turns out that in dimension n a smallest maximal decomposition has at most 2n−1 distinct summands.
Proposition 3.6
Let P⊂ℝn be a convex lattice polytope. Let Z be a smallest maximal decomposition in Z. Then Z has at most 2n−1 distinct summands.
Proof
Reduce all the summands in Z modulo 2. Since the summands are primitive segments, there will be 2n−1 possibilities for a reduced segment. If the number of distinct segments in Z is at least 2n, we will have two summands that are equal modulo 2. Then their sum is non-primitive, which contradicts the minimality of Z. □
Although we expect that the sum of the 2n−1 segments with 0,1 components mentioned in the proof of the above proposition has Minkowski length 2n−1, we do not have a proof of this statement, which would have implied that the bound of the proposition is sharp.
Let a lattice polytope P be described by its facets equations. Then Barvinok’s algorithm [1, 5] counts the number of lattice points in P in polynomial time. We will assume that the list P∩ℤ3 of the lattice points in P⊂ℝ3 is given, and will explain how to find the Minkowski length of P in polynomial time in P∩ℤ3.
Theorem 3.7
Let P⊂ℝ3 be a lattice polytope with the given set of its lattice points P∩ℤ3. Then the Minkowski length L(P) can be found in polynomial time in P∩ℤ3.
Proof
This algorithm relies on Theorem 3.5. We search for all possible decompositions of the form described in the theorem. For every quadruple of points {A,B,C,D}⊆P∩ℤ3, where it is important which point goes first and the order of the other three does not matter, we check if [0,B−A], [0,C−A], and [0,D−A] generate a parallelepiped of volume one or two. If the volume is one, these segments are equivalent to [0,e 1], [0,e 2], [0,e 3] and we look for maximal decompositions equivalent to

that is, maximal decompositions of the form
where E 1=[0,B−A], E 2=[0,C−A], E 3=[0,D−A], E 4=[0,B+C+D−3A], E 5=[0,B+C−2A] or [0,B−C], E 6=[0,B+D−2A], E 7=[0,C+D−2A].
If the volume is two, we check if the segments [0,B−A], [0,C−A], and [0,D−A] are primitive and if any two of them generate a parallelogram whose only lattice points are the vertices. If this is the case, these three segments are equivalent to [0,e 1], [0,e 2], and [0,e 1+e 2+2e 3]. We then let E 1=[0,B−A], E 2=[0,C−A], E 3=[0,D−A], E 4=[0,(B+C+D−3A)/2], E 5=[0,(B+D−C−3A)/2], E 6=[0,(C+D−B−3A)/2], E 7=[0,(D−A−B−C)/2].
Next, for every 1≤i≤7, we find M i , the largest integer such that there is some lattice point F in P with F+M i E i ⊆P. For each 7-tuple of integers m=(n 1,…,n 7) where 0≤n i ≤M i , we check if some lattice translate of the zonotope Z m =n 1 E 1+⋯+n 7 E 7 is contained in P (we run through lattice points F in P to check if F+Z m is contained in P). For all such zonotopes that fit into P we look at n 1+⋯+n 7 and find the maximal possible value N of this sum.
Finally, the largest such sum N over all choices of {A,B,C,D}⊆P∩ℤ3 is L(P). Clearly, this algorithm is polynomial in P∩ℤ3. □
A group of REU students (Ian Barnett, Benjamin Fulan, and Candice Quinn) at Kent State University in Summer 2011 tried to generalize this algorithm to dimension 4. Their first step was to obtain a 4D version of Proposition 3.4. They showed that if P⊆ℝ4 is a lattice polytope and Z=A+n 1 E 1+⋯+n l E l is a smallest maximal decomposition in P, then Vol(E i +E j +E k +E m )≤14 for any choice of 1≤i,j,k,m≤l, and this bound is sharp. Unfortunately, this bound is too high to obtain a description of smallest maximal decompositions in 4D, similar to the one of Proposition 3.5.
4 Lattice Polytopes of Minkowski Length 1
It was shown in Theorem 1.6 of [10] that if P⊇Q=Q 1+⋯+Q l is a maximal decomposition of a polygon P then at most one of Q i has an integer lattice point in its interior, that is, ∑I(Q i )≤1. This fact was crucial in [10] for establishing bounds on the minimum distance of the toric surface code defined by P. We expect that in order to extend these bounds to 3D codes, one needs to explore similar questions in dimension 3. As it was mentioned above, a description of polytopes of Minkowski length 1 in dimension 3 does not seem feasible. We will instead reduce the lattice segments contained in a 3D lattice polytope modulo 3, which will help us show that if P is a 3D polytope with L(P)=1, then ∑I(Q i ) is at most 4.
Let P be a lattice polytope in ℝ3 of Minkowski length 1. Then P has at most 8 lattice points. Indeed, otherwise there would have been two lattice points in P that are congruent modulo 2, and hence the segment connecting them would have Minkowski length of at least 2.
For each segment whose endpoints are lattice points in P, we consider its direction vector reduced modulo 3. Since v and −v define the same segment, we identify such vectors. For thus defined modulo three segments there are 13 equivalence classes:

that is, we are dealing with the projective space ℤ3ℙ2. Notice that if a,b, and c∈ℤ3ℙ2 are linearly independent (that is, a≠b, and c∉〈a,b〉={a,b,a±b}), they generate all the classes:

Let S be a five-point lattice set contained in a polytope of Minkowski length 1. There are ten lattice segments that connect lattice points in S. We will classify such sets S according to the numbers of segments from distinct classes in ℤ3ℙ2.
Proposition 4.1
If L(P)=1, then any 5-point lattice set S in P is of one of the following types.
-
4+2+2+2 The segments are from classes 4a,2b,2(a+b),2(a−b). Here a 4 or a 2 in front of segment’s class denotes its multiplicity, which is the number of times it occurs among the lattice segments in S.
-
3+3+2+2 The segments are from classes 3a,3b,2(a+b),2(a−b).
-
3+(7) The segments are from classes 3a,b,a+b,a−b,c,a+c,a−c,a+b−c.
-
2+2+(6) The segments are from classes 2a,2b,a+b,a−b,a+c,b+c,a+b+c,c.
-
(10) All ten lattice segments connecting points in S are from distinct classes in ℤ3ℙ2.
The elements a,b,c∈ℤ3ℙ2 in each of the type descriptions are linearly independent. All types except for the last one have segments from classes a,b,a+b,a−b.
Proof
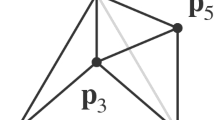
We assign direction to the segments by picking a standard representative from each of the classes. If two segments from the same class share a vertex, the arrows cannot both point to or away from the vertex as in this case the third side in the triangle is of Minkowski length at least 3. We also notice that if two sides in a triangle are from the same class, then the third one is also from that class and we get the triangle diagram below.

No other segment starting in one of these three vertices can be of class a, so the only remaining segment in S that could be of class a is the one connecting two remaining points of S. Hence the largest number of segments of the same class in S is 4. If we have 4 segments of the same class we get Fig. 3. We call this type 4+2+2+2 as there are four segments of one type and two segments of each of the three other types.
Next, assume we only have three segments from class a. Then they would have to form a triangle. We could also have another three segments of class b, forming a triangle sharing a vertex with the first triangle. Then there are three segments of class a, three of class b, and two of each of a+b and a−b. We call this type 3+3+2+2.
Assume next there is no other triangle. Connect one of the vertices of the triangle whose sides are of class a to a fourth lattice point in S. Let this segment be of class b. The segment connecting the fourth lattice point to the fifth cannot be from classes a,b,a+b, or a−b, as this would give either another triangle or four segments of the same class. Hence that segment is of class c, such that the set {a,b,c} is linearly independent and we get the diagram below. We call this type 3+(7) (see Fig. 4).
If there are no 3s but there is a 2, we get a configuration of type 2+2+(6) (see Fig. 5).
Finally, it is possible that there are no repeats among classes of segments. An example of this situation is a tetrahedron with the vertices (1,0,0), (0,1,0), (0,0,1), (−1,−1,−1) with one lattice point, the origin, strictly inside. We call this type (10). □
Lemma 4.2
Let a,b,c,d∈ℤ3ℙ2 where a≠b and c≠d. Then 〈a,b〉∩〈c,d〉≠∅.
Proof
If c∈〈a,b〉 the conclusion is obvious, so we can assume that 〈a,b,c〉=ℤ3ℙ2. One of d,c+d,c−d does not have c in its expression in terms of a,b,c, hence it belongs to 〈a,b〉. □
Proposition 4.3
Let P and Q be 3D lattice polytopes of Minkowski length 1 with at least five lattice points each. If there exists a 5-point lattice subset S of P of type 4+2+2+2 or 3+3+2+2, then L(P+Q)≥3.
Proof
Pick any 5-point lattice subset T of Q. Since in S we have used up four classes with multiplicities greater than 1, by Lemma 2.4, T cannot be of type (10), since the overall number of classes is 13. In S, we have multiple segments of each of the classes a, b, a+b, a−b for some a,b∈ℤ3ℙ2. Since T is not of type (10), we also have segments of classes c, d, c+d, c−d in T for some c,d∈ℤ3ℙ2, not necessarily with multiplicities. By Lemmas 4.2 and 2.4 we conclude L(P+Q)≥3. □
Proposition 4.4
Let P and Q be 3D lattice polytopes of Minkowski length 1. If there exist 3-point lattice subsets S and T of P and Q respectively, each of which forms a triangle with sides of the same class, then L(P+Q)≥3. In particular, if both S and T are of type 3+(7), then L(P+Q)≥3.
Proof
We first notice that if a lattice polytope contains a lattice triangle with sides of the same class, then this triangle is equivalent to T 0. Indeed, we can easily map this triangle to one in the (x,y)-plane by creating a matrix of determinant 1 whose last row is a primitive vector orthogonal to the plane of the triangle. We know that in the (x,y)-plane, up to the equivalence, there are only two triangles of length one, the unit triangle and T 0. The unit triangle has sides that belong to three distinct classes and the sides of T 0 are all from the same class. Hence the initial triangle is equivalent to T 0 and, therefore, has a lattice point inside and all four points are in the same plane.

We have such a configuration in both P and Q. Let the sides of the triangle in Q be of class c and one of the segments inside this triangle be of class d. By Lemma 4.2, P and Q share a segment. By Lemma 2.4, they cannot share a or c, so they have a common lattice segment inside the triangles. We can assume that b and d represent parallel segments. Notice that when extended to the intersection with the opposite side of T 0, these segments have Minkowski length 1.5, that is, if we add them up we get a segment of Minkowski length 3. Hence L(P+Q)≥3. For example, if P=Q=T 0 we get the diagram below.

□
Proposition 4.5
Let P and Q be 3D lattice polytopes of Minkowski length 1. If there exist 5-point lattice subsets S and T of P and Q of types 2+2+(6) and 3+(7) respectively, then L(P+Q)≥3.
Proof
We assume that L(P+Q)=2. Let the multiple classes in S be a and b and the class of multiplicity 3 in T be d. Let the triangle in T with all sides of class d be ABC and the remaining two lattice points in T be D and E with AD of class e and BE of class f, as depicted in the diagram below.

By Lemma 4.2, 〈a,b〉∩〈d,e〉≠∅ and 〈a,b〉∩〈d,f〉≠∅. Since classes a and b cannot occur in T and class d cannot occur in S, segments of classes a+b and a−b have to appear in T, and we can assume that e=a+b and f=a−b. This is because these two segments in T cannot share a vertex, as the third side in the triangle formed by a+b and a−b would have to be of class either a or b.
By Proposition 4.1, the segments connecting the lattice points in S are of classes a, b, a+b, a−b, a+c, b+c, a+b+c, and c for some linearly independent a,b,c∈ℤ3ℙ2. Hence there are five options left for d: a−c, b−c, a+b−c, a−b−c, a−b+c. Notice that in T we have segments of classes d+a+b, d−a−b, d−a+b, and d+a−b. Going through the five options for d, we observe that every time there are four lattice segments that are shared between S and T. Two of them are a+b and a−b. The remaining two for each of the five cases are listed in the table below.
d | Shared segments in S and T |
|---|---|
a−c | a−c−(a+b)=−(b+c),a−c+(a−b)=−(a+b+c) |
b−c | b−c−(a+b)=−(a+c),b−c−(a−b)=−(a+b+c) |
a+b−c | a+b−c−(a−b)=−(b+c),a+b−c+(a+b)=−(a+b+c) |
a−b−c | a−b−c−(a−b)=−c, a−b−c+(a+b)=−(a+c) |
a−b+c | a−b+c−(a−b)=c, a−b+c−(a+b)=b+c |
We have checked that there are always at least four segments shared between S and T, with the extra condition that in T none of these four segments is ED. In T, three of these segments cannot all have E as an endpoint, as this would imply that two of these segments in S also share an endpoint, so by Corollary 2.6 there is a shared triangle, one of whose sides is d, which is impossible. Similarly, three of the shared segments cannot all have D as an endpoint. Hence there are two possible scenarios, depicted in the diagram below. The shared segments are marked by a+b,a−b,x, and y.

In the first scenario, the triangle formed by x and y in S is shared, so its third side b is also shared, which leads to a contradiction. In the second scenario, two triangles, one formed by a+b and y, and another by a−b and x are shared, so their third side u appears twice in S, which is impossible. □
Proposition 4.6
Let P and Q be 3D lattice polytopes of Minkowski length 1. If there exist 5-point lattice subsets S and T of P and Q respectively, of type 2+2+(6) each, then L(P+Q)≥3.
Proof
We assume that L(P+Q)=2. Let the a and b be the classes of lattice segments in S of multiplicity 2. Then S also has segments of classes a+b and a−b. By Lemma 2.4 segments in T of multiplicity 2 cannot be of classes a,b,a+b,a−b, so we can assume that one of them is c and the other is a+b+c, by switching direction vectors of a, b, and c, if needed. Since we have 13 classes total, S and T overlap in at least three segments. One of them is of class a+b. We will show that S and T share three segments that form a triangle one of whose sides is of class either a+b or a−b.
Assume that the segment of class a−b is also shared. A segment of class a−b in T cannot share a vertex with a segment of class a+b (then either the sum or difference of those classes would also be represented in S, but classes a and b cannot appear in S). Changing direction of c and/or both a and b, we can assume that a−b is as in the diagram below.

Let the class of the third shared segment be x. Assume that in S the segment of class x shares a vertex with a−b. Then in T the segment of class x would have to share a vertex with a−b as the only ones that do not are c, a+b, and a+b+c and x cannot be one of them. Hence a−b and x share a vertex in both S and T and therefore by Corollary 2.6 S and T share a triangle with sides a−b, a+b−c, and a+c. Hence x=a+b−c and the diagrams for S and T are below.

We see that both S and T have triangles with a−c and a+c as sides, but those triangles are not identical, which contradicts L(P+Q)=2.
Next, let next x share a vertex with a+b in S. If x does not share a vertex with a+b in T as well, then the options for x are a+c and a+b−c. If x=a+c then either x−a=c or x+b=a+b+c is in S, which is impossible. If x=a+b−c, then either x+a+b=a+b+c or x−(a+b)=c is in S, which is also impossible. Hence a triangle with base a+b is shared between S and T, which leads to the same diagram and the same contradiction as before.
It remains to consider the case when a−b is not shared between S and T. We can also assume that a+b−c is not shared. (If it is shared replace S and T in the above argument.) Then S and T share two segments both of which have the fifth point as an endpoint in both S and T. Then the triangle formed by these two segments is shared and the base of that triangle is a+b. Notice that there is no room for other shared segments as they would have to have a fifth point as a vertex and a+b is the only option for shared base. Let us denote one of the shared segments by d. We get the diagram below.

We next search for the expression of d in terms of a,b and c so that the only common segments between S and T are a+b, d, and a+b+d. Below is the list of segments used in S and T.
S | T |
|---|---|
2a | 2c |
2b | 2(a+b+c) |
a+b | a+b |
a−b | a+b−c |
d | d |
d+a | d−c |
d+b | d+a+b+c |
d+a+b | d+a+b |
We clearly have d≠±a,±b,±(a+b),±(a−b),±c,±(a+b+c),±(a+b−c). All the remaining options are also very easy to get rid of. If d=±b+c,±a+c,±(a−b)+c, then d−c∈〈a+b〉. If d=−a−c, then d+a appears in both S and T. If d=−b−c, then d+b appears in both S and T. If d=a+b−c, then d+a+b appears in both S and T. If d=a−b−c, then d+a+b+c appears in both S and T. If d=a−c, then d+a is of the same class as d−c. Finally, if d=b−c, then d+b is of the same class as d−c. Every time we arrive at a contradiction, which proves the proposition. □
Proposition 4.7
Let P and Q be two 3D lattice polytopes of Minkowski length 1. If both P and Q are of type (10) and L(P+Q)=2, then P and Q are equal (the same up to translation).
Proof
Since there are 13 classes of segments total, P and Q share at least 7 segments. Among these shared segments we can find three that have a common endpoint in P. At least two of these three shared segments have a common endpoint in Q. Hence P and Q share a triangle ABC. Let the two remaining lattice points in P be D and E.
At least one of the two tetrahedra ABCD and ABCE with base ABC, say, ABCD, has at least two lateral edges that are shared. Together with a segment in the base these two edges form a triangle with shared sides. At least two of these three shared sides share a vertex in Q, so by Corollary 2.6 we get a shared triangle. We have shown that P and Q have two pairs of shared triangles that have a common edge, so P and Q share a tetrahedron ABCD. Let the fifth vertices in P and Q be E and E′.
Since P and Q share at least seven lattice segments, there is a segment in P connecting one of A,B,C,D to E which is shared with Q. Let this segment be AE. The parallel segment in Q is of the form E′X where X=A,B,C, or D. In any of these cases, AE and E′X are adjacent to a shared segment AX, so triangles AEX and AE′X are translates of each other, which implies that P and Q are the same up to a translation. □
Proposition 4.8
Let P and Q be 3D lattice polytopes of Minkowski length 1. If there exist 5-point lattice subsets S and T of P and Q of types 3+(7) and (10) respectively, then L(P+Q)≥3.
Proof
We assume that L(P+Q)=2. There are 13 classes of segments total, so S and T have to share at least five segments. Let S have lattice points A, B, C, D, and E, where ABC is a triangle with sides of the same class and D a point inside that triangle. If AE, BE, and CE are all shared with T, then two of them share a vertex in T and hence one of the triangles ABE, ACE, or BCE is shared, which is impossible since sides of ABC cannot be shared. Hence one of AE, BE, CE is not shared. Similarly, one of AD, BD, CD is not shared. This implies that ED is shared, and we can assume that ADE is a shared triangle, DB and EC are shared, while DC and EB are not shared.

Then b and b+c−a in T should not be adjacent to ED (or either DC or EB would be shared). Hence one of b, b+c−a has A as an endpoint in T. If it is b, we have either a or a−b in T; if it is b+c−a, then either b+c or a is in T. Both of these options are impossible. □
Proposition 4.9
Let P and Q be 3D lattice polytopes of Minkowski length 1. If there exist 5-point lattice subsets S and T of P and Q of types 2+2+(6) and (10) respectively, then L(P+Q)≥3.
Proof
We assume that L(P+Q)=2. There are 13 classes of segments total, so S and T have to share at least five segments. Let S have lattice points A, B, C, D, and E, where AB and CD are from the same class, and BC and AD are from the same class. At least three segments starting at E are shared. In T at least two of them share a vertex, hence S and T share a triangle with vertex E. We can assume that triangle is AEC. One of EB, ED is also shared, let us assume it is EB. This segment in T cannot share a vertex with AE or EC (this would imply that either AB or BC is shared), so it connects two remaining vertices X and Y. If ED is also shared, same would be true, but there are only five vertices, so ED is not shared. Hence BD is shared. But it would have to have either X or Y as one of the vertices, hence EBD is shared, a contradiction. □
Theorem 4.10
Let P, Q, R be three 3D lattice polytopes of Minkowski length 1 with at least five lattice points each. Then L(P+Q+R)≥4.
Proof
Let S,T, and U be any 5-point lattice subsets of P, Q, and R correspondingly. By the above propositions, S, T, and U are all of type (10). If any of the three polytopes has more than five points, then there are at least 15 lattice segments connecting them. Hence there are multiple segments of the same class. Reducing the number of points, we get sets S, T, and U where at least one of these lattice sets is not of type (10).
Hence we can assume that each of P, Q, and R has exactly five lattice points and is of type (10). Furthermore, all three polytopes are translates of each other. It remains to show that L(3P)≥4.
Let us assume first that P has four lattice vertices A,B,C,D and a lattice point E inside. Let G be the centroid of P. Draw through G four planes, each parallel to one of the facets of P. Each of the planes cuts off a tetrahedron off of P, which is similar to P with a coefficient of 3/4. These four tetrahedra cover P, so the interior lattice point E belongs to at least one of them, say, to the tetrahedron one of whose vertices is A. Then if we continue AE to the point of intersection F with the plane BCD, then AE/AF≤3/4 and 3AF≥4AE, so in 3P we have a segment 3AF whose lattice length is at least 4. We have shown that in this case L(3P)≥4.
Next, let P of type (10) have five lattice vertices and no other lattice points. It was shown in [9], Theorem 3.5 that P is \(\operatorname {AGL}(3,\mathbb {Z})\) equivalent to a polytope with the vertices (0,0,0), (1,0,0), (0,1,0), (0,0,1), and (1,a,b) where gcd(a,b)=1 and 0≤a≤b. The sum of the two segments, [0,a,b] and [0,1,0] is a parallelogram of area b. If b≥3 then by Lemma 1.7 of [10] the Minkowski length of this parallelogram is at least 3 and hence L(2P)≥3. We are left with two cases a=b=1 and a=1, b=2 (if a=0 then L(P)≠1). In the second case P is not of type (10) as (0,a,b)=(0,1,−1). It remains to deal with the case a=b=1. Let I be the vertical segment of length 1 and let J be the segment connecting the origin to (1,1,0). Then I+1/2J⊆P and hence 2I+J⊆2P, so we again have L(2P)≥3. □
Notice that we have also proved the following Corollary.
Corollary 4.11
If P and Q are 3D lattice polytopes of Minkowski length 1 with at least five lattice points each, then L(P+Q)≥3 unless P and Q are of type (10) and are the same up to translation.
Next example demonstrates that one could have L(2P)=2 for a 3D lattice polytope P of type (10).
Example 4.12
Let P have the vertices (−1,−1,−1), (1,0,0), (0,1,0), and (0,0,1). Then P is of type (10), L(P)=1, and L(2P)=2.
Proposition 4.13
Let P and Q be 3D lattice polytopes of Minkowski length 1. If P has at least six lattice points and Q has at least five, then L(P+Q)≥3.
Proof
Since P has six lattice points, there are 15 lattice segments in P. Since there are 13 classes total, some of the segments will repeat and we will either have two segments of the same class not sharing endpoints, or three segments of the same class forming a triangle. Hence we can pick five points in P that form a lattice subset of type other than (10), which implies L(P+Q)≥3. □
Theorem 4.14
Let Q 1+⋯+Q N ⊆P be a maximal decomposition. Let I(Q i ) denote the number of interior lattice points with respect to the 3D topology. Then the overall number of interior lattice points
Furthermore, if more than one Q i has interior lattice points with respect to the 3D topology, we have I≤2.
Proof
In order to have an interior lattice point with respect to the 3D topology, Q i has to have at least five lattice points. Hence, by Theorem 4.10, at most two of the Q i ’s could have interior lattice points and be three-dimensional. Let us assume that this holds for two of the Q i ’s. If one of these two Q i ’s has at least two interior lattice points, we get a contradiction with Proposition 4.13. Hence in this case the total number of interior lattice points is at most 2. If only one of the Q i ’s has interior lattice points with respect to the 3D topology, then there are at most four of them, as L(Q i )=1 and Q i has at most eight lattice points total. □
The following example shows that there exists a Minkowski length one 3D polytope that has four interior lattice points, so the bound of Theorem 4.14 is sharp.
Example 4.15
Consider a simplex P with the vertices (0,0,0), (1,3,0), (0,2,3), and (4,1,3). Then the interior lattice points of P are (1,2,1), (1,2,2), (1,1,1), and (2,1,2). This can be checked by hand or using Polymake [2]. It is easy to verify that there are no parallel lattice segments connecting lattice points in P, which implies that L(P)=1.
An example of a 3D lattice polytope of Minkowski length one with 8 lattice points (all of them on the boundary) was given in an MSRI-UP project directed by John Little [11]. The number of lattice points in a lattice polytope in the n-space is at most 2n. A group of REU students at Kent in Summer 2011 constructed a lattice n-dimensional Minkowski length one polytope with 2n points. It would be interesting to see if there exists an n-dimensional simplex that has 2n lattice points and Minkowski length one.
References
Alexander, I.B.: Polynomial time algorithm for counting integral points in polyhedra when the dimension is fixed. Math. Oper. Res. 19, 769–779 (1994)
Gawrilow, E., Joswig, M.: Polymake: a framework for analyzing convex polytopes. In: Polytopes–Combinatorics and Computation, Oberwolfach, 1997. DMV-Sem, vol. 29, pp. 43–73. Birkhäuser, Basel (2000)
Hansen, J.P.: Toric surfaces and error-correcting codes. In: Coding Theory, Cryptography and Related Areas, Guanajuato, 1998, pp. 132–142. Springer, Berlin (2000)
Kasprzyk, A.M.: Toric Fano three-folds with terminal singularities. Tohoku Math. J. (2) 58(1), 101–121 (2006)
Köppe, M.: A primal Barvinok algorithm based on irrational decompositions. SIAM J. Discrete Math. 21, 220–236 (2007)
Little, J., Schenck, H.: Toric surface codes and Minkowski sums. SIAM J. Discrete Math. 20(4), 999–1014 (2006) (electronic)
Newman, M.: Integral Matrices. Pure and Applied Mathematics, vol. 45. Academic Press, San Diego (1972) ISBN-13:978-0125178501, 224 pp.
Ruano, D.: On the parameters of r-dimensional toric codes. Finite Fields Appl. 13(4), 962–976 (2007)
Scarf, H.E.: Integral polyhedra in three space. Math. Oper. Res. 10(3), 403–438 (1985)
Soprunov, I., Soprunova, J.: Toric surface codes and Minkowski length of polygons. SIAM J. Discrete Math. 23(1), 384–400 (2008/09)
Gaudinez, A., Outing, C., Vega, R.: Indecomposable polyhedra and toric codes. MSRI-UP 2009 Technical report, http://www.msri.org/web/msri/scientific/workshops/show/-/event/Wm491 45-57
Acknowledgements
We are thankful to the anonymous referee for pointing out a gap in one of the arguments as well as for numerous corrections and suggestions.
The authors were supported by funds from NSF-REU Grant DMS-0755318.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Beckwith, O., Grimm, M., Soprunova, J. et al. Minkowski Length of 3D Lattice Polytopes. Discrete Comput Geom 48, 1137–1158 (2012). https://doi.org/10.1007/s00454-012-9433-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-012-9433-5