Length of Longest Cycles in a Graph Whose Relative Length is at Least Two | Graphs and Combinatorics Skip to main content
Springer Nature Link
Log in

Length of Longest Cycles in a Graph Whose Relative Length is at Least Two

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

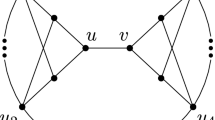
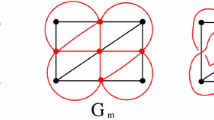
Abstract

Let G be a graph. We denote p(G) and c(G) the order of a longest path and the order of a longest cycle of G, respectively. Let κ(G) be the connectivity of G, and let σ 3(G) be the minimum degree sum of an independent set of three vertices in G. In this paper, we prove that if G is a 2-connected graph with p(G) − c(G) ≥ 2, then either (i) c(G) ≥ σ 3(G) − 3 or (ii) κ(G) = 2 and p(G) ≥ σ 3(G) − 1. This result implies several known results as corollaries and gives a new lower bound of the circumference.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bauer D., Broersma H.J., van den Heuvel J., Veldman H.J.: Long cycles in graphs with prescribed toughness and minimum degree. Discrete Math. 141, 1–10 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bermond J.C.: On hamiltonian walks. Congr. Numer. 15, 41–51 (1976)

    MathSciNet  Google Scholar 

  3. Bondy, J.A.: Longest paths and cycles in graphs with high degree, Research Report CORR 80-16, Department of Combinatorics and Optimization, University of Waterloo, Waterloo (1980)

  4. Bondy J.A.: Basic graph theory: paths and circuits. In: Graham, R., Grőtshel, M., Lovász, L. (eds) Handbook of Combinatorics, vol. I, pp. 5–110. Elsevier, Amsterdam (1995)

    Google Scholar 

  5. Bondy J.A., Locke S.C.: Relative length of paths and cycles in 3-connected graphs. Discrete Math. 33, 111–122 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dirac G.A.: Some theorems on abstract graphs. Proc. Lond. Math. Soc. 2, 69–81 (1952)

    Article  MathSciNet  MATH  Google Scholar 

  7. Egawa Y., Miyamoto T.: The longest cycles in a graph G with minimum degree at least |G|/k. J. Combin. Theory Ser. B 46, 356–362 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  8. Ellingham M.N., Menser D.K.: Girth, minimum degree, and circumference. J. Graph Theory 34, 221–233 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  9. Enomoto H., van den Heuvel J., Kaneko A., Saito A.: Relative length of long paths and cycles in graphs with large degree sums. J. Graph Theory 20, 213–225 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  10. Faudree R.J., Gould R.J., Jacobson M.S., Schelp R.H.: Extremal problems involving neighborhood unions. J. Graph Theory 11, 555–564 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fournier I., Fraisse P.: On a conjecture of Bondy. J. Combin. Theory Ser. B 39, 17–26 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  12. Fraisse P., Jung H.A.: Longest cycles and independent sets in k-connected graphs. In: Kulli, V.R. (eds) Recent Studies in Graph Theory, pp. 114–139. Vischwa International Publishing Gulbarga, India (1989)

    Google Scholar 

  13. Jung H.A., Witmann P.: Longest cycles in tough graphs. J. Graph Theory 31, 107–127 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  14. Li R., Saito A., Schelp R.H.: Relative length of longest paths and cycles in 3-connected graphs. J. Graph Theory 37, 137–156 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  15. Linial N.: A lower bound for the circumference of a graph. Discrete Math. 15, 297–300 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  16. Liu X.: Lower bounds of length of longest cycles in graphs involving neighborhood unions. Discrete Math. 169, 133–144 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  17. Ore O.: On a graph theorem by Dirac. J. Combin. Theory 2, 383–392 (1967)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ozeki K., Tsugaki M., Yamashita T.: On relative length of longest paths and cycles. J. Graph Theory 62, 279–291 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Saito A.: Long paths, long cycles and their relative length. J. Graph Theory 30, 91–99 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  20. Voss, H.-J.: Cycles and bridges in graphs. In: Mathematics and its Applications (East European Series), vol. 19, Kluwer Academic Publishers, Dordrecht (1991)

  21. Zhang C.Q.: Circumference and girth. J. Graph Theory 13, 485–490 (1989)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo, 101-8430, Japan

    Kenta Ozeki

  2. Department of Mathematics, Kinki University, Kowakae 3-4-1, Higashiosaka, Osaka, 577-8502, Japan

    Tomoki Yamashita

Authors
  1. Kenta Ozeki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tomoki Yamashita
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kenta Ozeki.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ozeki, K., Yamashita, T. Length of Longest Cycles in a Graph Whose Relative Length is at Least Two. Graphs and Combinatorics 28, 859–868 (2012). https://doi.org/10.1007/s00373-011-1078-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-011-1078-2

Keywords

Search

Navigation