Abstract.
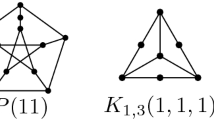
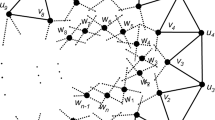
Thomassen proposed a well-known conjecture: every 4-connected line graph is hamiltonian. In this note, we show that Thomassen’s conjecture is equivalent to the statement that the shortness coefficient of the class of all 4-connected line graphs is one and the statement that the shortness coefficient of the class of all 4-connected claw-free graphs is one respectively.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Author information
Authors and Affiliations
Corresponding author
Additional information
Research partially supported by the fund of the basic research of Beijing Institute of Technology, by the fund of Natural Science of Jiangxi Province and by grant No. LN00A056 of the Czech Ministry of Education
Rights and permissions
About this article
Cite this article
Xiong, L., Kužel, R. A Note on the Shortness Coefficient and the Hamiltonicity of 4-Connected Line Graphs. Graphs and Combinatorics 21, 137–144 (2005). https://doi.org/10.1007/s00373-004-0595-7
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s00373-004-0595-7
Keywords
- Thomassen’s conjecture
- Line graph
- Dominating cycle conjecture
- Essentially edge connected graph
- Shortness coefficient