The Kumaraswamy distribution: median-dispersion re-parameterizations for regression modeling and simulation-based estimation | Statistical Papers Skip to main content
Springer Nature Link
Log in

The Kumaraswamy distribution: median-dispersion re-parameterizations for regression modeling and simulation-based estimation

  • Regular Article
  • Published:
Statistical Papers Aims and scope Submit manuscript

Abstract

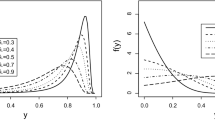
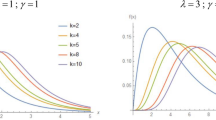
The Kumaraswamy distribution is very similar to the Beta distribution, but has the important advantage of an invertible closed form cumulative distribution function. The parameterization of the distribution in terms of shape parameters and the lack of simple expressions for its mean and variance hinder, however, its utilization with modeling purposes. The paper presents two median-dispersion re-parameterizations of the Kumaraswamy distribution aimed at facilitating its use in regression models in which both the location and the dispersion parameters are functions of their own distinct sets of covariates, and in latent-variable and other models estimated through simulation-based methods. In both re-parameterizations the dispersion parameter establishes a quantile-spread order among Kumaraswamy distributions with the same median and support. The study also describes the behavior of the re-parameterized distributions, determines some of their limiting distributions, and discusses the potential comparative advantages of using them in the context of regression modeling and simulation-based estimation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramowitz M, Stegun IA (eds) (1972) Handbook of mathematical functions with formulas, graphs, and mathematical tables (9th edn). New York, Dover

  • Balanda K, MacGillivray H (1990) Can J Stat 18(1): 17–30

    Article  MathSciNet  MATH  Google Scholar 

  • Bickel PJ, Lehmann EL (1979) Descriptive statistics for nonparametric models IV. Spread. In: Jurečková J (ed). Contributions to statistics. D. Reidel, Dordrecht and Boston

  • Brehm J, Gates S (1993) Donut shops and speed traps: evaluating models of supervision on police behavior. Am J Political Sci 37(2): 555–581

    Article  Google Scholar 

  • Cameron A, Trivedi P (2005) Microeconometrics. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Courard-Hauri D (2007) Using Monte Carlo analysis to investigate the relationship between overconsumption and uncertain access to one’s personal utility function. Ecol Econ 64(1): 152–162

    Article  Google Scholar 

  • Cribari-Neto F, Souza T (Forthcoming) Testing inference in variable dispersion beta regressions. J Stat Comput Simul

  • Cribari-Neto F, Zeileis A (2010) Beta regression in R. J Stat Software 34(2): 1–24

    Google Scholar 

  • Devroye L (1986) Non-uniform random variate generation. Springer-Verlag, New York

    MATH  Google Scholar 

  • Espinheira PL, Ferrari SLP, Cribari-Neto F (2008a) Influence diagnostics in beta regression. Comput Stat Data Anal 52(9): 4417–4431

    Article  MathSciNet  MATH  Google Scholar 

  • Espinheira PL, Ferrari SLP, Cribari-Neto F (2008b) On beta regression residuals. J Appl Stat 35(4): 407–419

    Article  MathSciNet  MATH  Google Scholar 

  • Fernandez-Ponce JM, Kochar SC, Muñoz-Perez J (1998) Partial orderings of distributions based on right-spread functions. J Appl Prob 35: 221–228

    Article  MATH  Google Scholar 

  • Ferrari SLP, Cribari-Neto F (2004) Beta regression for modeling rates and proportions. J Appl Stat 31(7): 799–815

    Article  MathSciNet  MATH  Google Scholar 

  • Ferrari SLP, Espinheira PL, Cribari-Neto F (2011) Diagnostic tools in beta regression with varying dispersion. Statistica Neerlandica 65(3): 337–351

    Article  MathSciNet  MATH  Google Scholar 

  • Fletcher SC, Ponnambalam K (1996) Estimation of reservoir yield and storage distribution using moments analysis. J Hydrol 182(1–4): 259–275

    Article  Google Scholar 

  • Gallant AR, Tauchen G (1996) Which moments to match. Econom Theory 12: 657–681

    Article  MathSciNet  Google Scholar 

  • Ganji A, Ponnambalam K, Khalili D, Karamouz M (2006) Grain yield reliability analysis with crop water demand uncertainty. Stoch Environ Res Risk Assess 20(4): 259–277

    Article  MathSciNet  Google Scholar 

  • Garg M (2008) On distribution of order statistics from Kumaraswamy distribution. Kyunpook Math J 48: 411–417

    Article  MATH  Google Scholar 

  • Gouriéroux C, Monfort A (1996) Simulation-based econometric methods. Oxford University Press, Oxford

    Google Scholar 

  • Green WH (2007) Censored data and truncated distributions. In: Mills T, Patterson K (eds) The handbook of econometrics, Vol 1. Palgrave, London

  • Hao L, Naiman D (2007) Quantile regression. Sage, Thousand Oaks

  • He X (1997) Quantile curves without crossing. Am Stat 51(2): 186–192

    Google Scholar 

  • Hickey R (1986) Concepts of dispersion in distributions: a comparative note. J Appl Prob 23(4): 914–921

    Article  MathSciNet  MATH  Google Scholar 

  • Johnson N, Kotz S, Balakrishnan N (1995) Continuous univariate distributions. Wiley, New York

    MATH  Google Scholar 

  • Jones MC (2009) Kumaraswamy’s distribution: a beta-type distribution with some tractability advantages. Stat Methodol 6(1): 70–81

    Article  MathSciNet  MATH  Google Scholar 

  • Kieschnick R, McCullough B (2003) Regression analysis of variates observed on (0, 1): percentages, proportions and fractions. Stat Model 3: 193–213

    Article  MathSciNet  Google Scholar 

  • King G, Tomz M, Wittenberg J (2000) Making the most of statistical analyses: improving interpretation and presentation. Am J Political Sci 44(2): 341–355

    Article  Google Scholar 

  • Koenker R (2005) Quantile regression. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Kumaraswamy P (1980) A generalized probability density function for double-bounded random processes. J Hydrol 46: 79–88

    Article  Google Scholar 

  • Lewis T, Thompson JW (1981) Dispersive distributions and the connections between dispersivity and strong unimodality. J Appl Prob 18(1): 76–90

    Article  MathSciNet  MATH  Google Scholar 

  • Little R, Rubin D (2002) Statistical analysis with missing data (2nd edn). Wiley, Hoboken

  • Machado J, Santos Silva JMC (2010) Quantiles with corners. Unpublished.

  • Manski C (1991) Regression. J Econ Lit 29(1): 34–50

    Google Scholar 

  • McCullagh P, Nelder J (1989) Generalized linear models. Chapman & Hall, London

    MATH  Google Scholar 

  • McDonald J (1984) Some generalized functions for the size distribution of income. Econometrica 52(3): 647–665

    Article  MATH  Google Scholar 

  • Mielke PW Jr. (1975) Convenient beta distribution likelihood techniques for describing and comparing meteorological data. J Appl Meteorol 14: 985–990

    Article  Google Scholar 

  • Mitnik P (Forthcoming). New properties of the Kumaraswamy distribution. Commun Stat: Theory Method

  • Nadarajah S (2008) On the distribution of Kumaraswamy. J Hydrol 348: 568–569

    Article  Google Scholar 

  • Nagypál É (2007) Learning by doing vs.. learning about match quality: can we tell them apart? Rev Econ Stud 74: 537–566

    MATH  Google Scholar 

  • Ospina R, Cribari-Neto F, Vasconcellos K (2006) Improved point and interval estimation for a beta regression model. Comput Stat Data Anal 51: 960–981

    Article  MathSciNet  MATH  Google Scholar 

  • Paolino P (2001) Maximum likelihood estimation of models with beta-distributed dependent variables. Political Anal 9(4): 325–346

    Article  Google Scholar 

  • Pham-Gia T, Hung TL (2001) The mean and median absolute deviations. Math Comput Model 34: 921–936

    Article  MathSciNet  MATH  Google Scholar 

  • Roberto M, Schuermann T, Weeks M (2000) Simulation-based inference in econometrics: methods and applications. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Rocha AV, Simas AB (2011) Influence diagnostics in a general class of beta regression models. Test 20: 95–119

    Article  MathSciNet  Google Scholar 

  • Sanchez S, Ancheyta J, McCaffrey WC (2007) Comparison of probability distribution functions for fitting distillation curves of petroleum. Energy & Fuels 21(5): 2955–2963

    Article  Google Scholar 

  • Seifi A, Ponnambalam K, Vlach J (2000) Maximization of manufacturing yield of systems with arbitrary distributions of component values. Ann Oper Res 99: 373–383

    Article  MathSciNet  MATH  Google Scholar 

  • Shaked M, Shanthikumar G (2007) Stochastic orders. Springer, New York

    Book  MATH  Google Scholar 

  • Simas AB, Barreto-Souza W, Rocha AV (2010) Improved estimators for a general class of beta regression models. Comput Stat Data Anal 54(2): 348–366

    Article  MathSciNet  MATH  Google Scholar 

  • Smithson M, Verkuilen J (2006) A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol Method 11(1): 54–71

    Article  Google Scholar 

  • Smyth G (1989) Generalized linear models with varying dispersion. J R Stat Soc, Ser B 51(1): 47–60

    MathSciNet  Google Scholar 

  • Sundar V, Subbiah K (1989) Application of double bounded probability density-function for analysis of ocean waves. Ocean Eng 16(2): 193–200

    Article  Google Scholar 

  • Townsend J, Colonius H (2005) Variability of the max and min statistic: a theory of the quantile spread as a function of sample size. Psychometrika 70(4): 759–772

    Article  MathSciNet  Google Scholar 

  • van Dorp JR, Mazzuchi T (2004) Parameter specification of the beta distribution and its dirichlet extensions utilizing quantiles. In: Gupta A, Nadarajah S (eds). Handbook of beta distribution and its applications. Marcel Dekker, New York

  • Vasconcellos K, Cribari-Neto F (2005) Improved maximum likelihood estimation in a new class of beta regression models. Braz J Prob Stat 19: 13–31

    MathSciNet  Google Scholar 

  • Yamaguchi S (2007) Job search, bargaining, and wage dynamics, ISER Discussion Paper # 658. Institute of Social and Economic Research, Osaka University, Osaka

Download references

Author information

Authors and Affiliations

  1. Center for the Study of Poverty and Inequality, Stanford University, 450 Serra Mall, Building 370, Room 212, Stanford, CA, 94305-2029, USA

    Pablo A. Mitnik & Sunyoung Baek

Authors
  1. Pablo A. Mitnik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sunyoung Baek
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pablo A. Mitnik.

Electronic Supplementary Material

The Below is the Electronic Supplementary Material.

ESM 1 (DOCX 54 kb)

ESM 2 (DOCX 23 kb)

ESM 3 (DOCX 102 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mitnik, P.A., Baek, S. The Kumaraswamy distribution: median-dispersion re-parameterizations for regression modeling and simulation-based estimation. Stat Papers 54, 177–192 (2013). https://doi.org/10.1007/s00362-011-0417-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00362-011-0417-y

Keywords

Mathematics Subject Classifications (2000)

Search

Navigation