Abstract
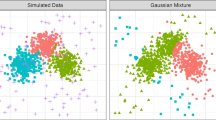
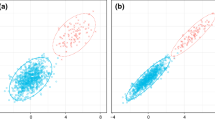
In model-based clustering based on normal-mixture models, a few outlying observations can influence the cluster structure and number. This paper develops a method to identify these, however it does not attempt to identify clusters amidst a large field of noisy observations. We identify outliers as those observations in a cluster with minimal membership proportion or for which the cluster-specific variance with and without the observation is very different. Results from a simulation study demonstrate the ability of our method to detect true outliers without falsely identifying many non-outliers and improved performance over other approaches, under most scenarios. We use the contributed R package MCLUST for model-based clustering, but propose a modified prior for the cluster-specific variance which avoids degeneracies in estimation procedures. We also compare results from our outlier method to published results on National Hockey League data.
Similar content being viewed by others
References
BANFIELD, J., and RAFTERY, A. (1993), “Model-Based Gaussian and Non-Gaussian Clustering”, Biometrics, 49(3), 803–821.
BREUNIG, M., KRIEGEL, H., NG, R., and SANDER, J. (2000), “LOF: Identifying Density-Based Local Outliers”, Sigmod Record, 29(2), 93–104.
BYERS, S., and RAFTERY, A. E. (1998), “Nearest-Neighbor Clutter Removal for Estimating Features in Spatial Point Processes”, Journal of the American Statistical Association, 93(442), 577–584.
CELEUX, G., and GOVAERT, G. (1995), “Gaussian Parsimonious Clustering Models”, Pattern Recognition, 28(5), 781–793.
CORETTO, P., and HENNIG, C. (2011), “Maximum Likelihood Estimation of Heterogeneous Mixtures of Gaussian and Uniform Distributions,” Journal of Statistical Planning and Inference, 141(1), 462–473.
FRALEY, C., and RAFTERY, A. (1999), “MCLUST: Software for Model-Based Cluster Analysis”, Journal of Classification, 16(2), 297–306.
FRALEY, C., and RAFTERY, A. (2006), “MCLUST Version 3 for R: Normal Mixture Modeling and Model-Based Clustering”, Technical report, University of Washington.
FRALEY, C., and RAFTERY, A. (2007), “Bayesian Regularization for Normal Mixture Estimation and Model-Based Clustering”, Journal of Classification, 24(2), 155–181.
GNANADESIKAN, R. (1989), “Discriminant Analysis and Clustering: Panel on Discriminant Analysis, Classification, and Clustering”, Statistical Science, 4(1), 34–69.
HARDIN, J., and ROCKE, D. (2002), “Outlier Detection in the Multiple Cluster Setting Using the Minimum Covariance Determinant Estimator”, Computational Statistics and Data Analysis, 44(4), 625–638.
HE, Z., XU, X., and DENG, S. (2003), “Discovering Cluster-Based Local Outliers”, Pattern Recognition Letters, 24(9–10), 1641–1650.
HENNIG, C. (2004), “Breakdown Points for Maximum Likelihood Estimators of Location Scale Mixtures”, The Annals of Statistics, 32(4), 1313–1340.
HENNIG, C., and CORETTO, P. (2008), “The Noise Component in Model-Based Cluster Analysis”, in Data Analysis, Machine Learning and Applications, eds. C. Preisach,
H. Burkhardt, L. Schmidt-Thieme, and R. Decker, Berlin Heidelberg: Springer, pp. 127–138.
KNORR, E., and NG, R. (1998), “Algorithms for Mining Distance-Based Outliers in Large Datasets”, in VLDB ’98 Proceedings of the 24th International Conference on Very Large Data Bases, San Francisco: Morgan Kaufmann, pp. 392–403.
KRIEGEL, H., KR ÖGER, P., SCHUBERT, E., and ZIMEK, A. (2009), “Loop: Local Outlier Probabilities”, in Proceedings of the 18th ACM Conference on Information and Knowledge Management, New York: ACM, pp. 1649–1652.
KRIEGEL, H., KR ÖGER, P., SCHUBERT, E., and ZIMEK, A. (2011), “Interpreting and Unifying Outlier Scores”, in Proceedings of the SIAM International Conference on Data Mining, pp. 13–24.
PEEL, D., and MCLACHLAN, G.J. (2000), “Robust Mixture Modelling Using the t Distribution”, Statistics and Computing, 10(4), 339–348.
REHM, F., KLAWONN, F., and KRUSE, R. (2007), “A Novel Approach to Noise Clustering for Outlier Detection”, Soft Computing-A Fusion of Foundations, Methodologies and Applications, 11(5), 489–494.
ROUSSEEUW, P., and VAN ZOMEREN, B. (1990), “Unmasking Multivariate Outliers and Leverage Points”, Journal of the American Statistical Association, 85(411), 633–639.
SHOTWELL, M., and SLATE, E. (2011), “Bayesian Outlier Detection with Dirichlet Process Mixtures”, Bayesian Analysis, 6(4), 665–690.
SVENSÉN, M., and BISHOP, C. (2005), “Robust Bayesian Mixture Modelling”, Neurocomputing, 64, 235–252.
WANG, N., and RAFTERY, A.E. (2002), “Nearest-Neighbor Variance Estimation (NNVE)”, Journal of the American Statistical Association, 97(460), 994–1019.
Author information
Authors and Affiliations
Corresponding author
Additional information
The work on this paper was completed while K. Evans was finishing her PhD at the University of Rochester, Rochester USA.
Rights and permissions
About this article
Cite this article
Evans, K., Love, T. & Thurston, S.W. Outlier Identification in Model-Based Cluster Analysis. J Classif 32, 63–84 (2015). https://doi.org/10.1007/s00357-015-9171-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00357-015-9171-5