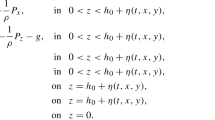Model Equations and Traveling Wave Solutions for Shallow-Water Waves with the Coriolis Effect

Abstract

In the present study, we start by formally deriving the simplified phenomenological models of long-crested shallow-water waves propagating in the equatorial ocean regions with the Coriolis effect due to the Earth’s rotation. These new model equations are analogous to the Green–Naghdi equations, the first-order approximations of the KdV-, or BBM type, respectively. We then justify rigorously that in the long-wave limit, unidirectional solutions of a class of KdV- or BBM type are well approximated by the solutions of the Camassa–Holm equation in a rotating setting. The modeling and analysis of those mathematical models then illustrate that the Coriolis forcing in the propagation of shallow-water waves can not be neglected. Indeed, the CH-approximation with the Coriolis effect captures stronger nonlinear effects than the nonlinear dispersive rotational KdV type. Furthermore, we demonstrate nonexistence of the Camassa–Holm-type peaked solution and classify various localized traveling wave solutions to the Camassa–Holm equation with the Coriolis effect depending on the range of the rotation parameter.

Appendix

1.1 Classification of Traveling Wave Solutions

Our attention in this appendix is now turned to investigate if there are any other peaked traveling wave solutions in certain parametric ranges, but not that particular form negated by Theorem 4.1. Existence of those kinds of peaked traveling wave solutions is confirmed in Theorem 5.1.

We now classify the traveling wave solutions to the R-CH equation (4.1). For a traveling wave solution $\varphi (t,x) = \varphi (x-\sigma t)$ with speed $\sigma$, Eq. (4.1) takes the form

$$\begin{aligned} -\sigma \varphi _{x} + \sigma \varphi _{xxx} + c\varphi _{x} + 3\varphi \varphi _{x} -\frac{\beta _0}{\beta }\varphi _{xxx} + \frac{\omega _1}{\alpha ^2}\varphi ^2\varphi _{x} + \frac{\omega _2}{\alpha ^3}\varphi ^3\varphi _{x} = 2\varphi _{x}\varphi _{xx} + \varphi \varphi _{xxx}. \end{aligned}$$

(5.1)

Integrating respect to spatial variable gives

$$\begin{aligned} (c-\sigma )\varphi + \frac{3}{2}\varphi ^2 + \frac{\omega _1}{3\alpha ^2}\varphi ^3 + \frac{\omega _2}{4\alpha ^3}\varphi ^4 + \left( \sigma -\frac{\beta _0}{\beta }\right) \varphi _{xx} - \frac{1}{2}(\varphi _{x})^2 - \varphi \varphi _{xx} = 0, \end{aligned}$$

(5.2)

for $|x|\rightarrow \infty$, $\varphi , \varphi _{x}, \varphi _{xx}\rightarrow 0$.

It is observed that

$$\begin{aligned} \left[ \left( \varphi -\sigma +\frac{\beta _0}{\beta }\right) ^2\right] _{xx} = 2\varphi _{x}^2 + 2\varphi \varphi _{xx} - 2\left( \sigma -\frac{\beta _0}{\beta }\right) \varphi _{xx}. \end{aligned}$$

Equation (5.2) may take the following form

$$\begin{aligned} \left[ \left( \varphi -\sigma +\frac{\beta _0}{\beta }\right) ^2\right] _{xx} = \varphi _{x}^2 + 3\varphi ^2 + \frac{2\omega _1}{3\alpha ^2}\varphi ^3 + \frac{\omega _2}{2\alpha ^3}\varphi ^4 + 2(c-\sigma )\varphi . \end{aligned}$$

(5.3)

Inspired by the approach of classification of the traveling wave solutions to the classical Camassa–Holm equation (Lenells 2005), we can establish a similar result in the following lemma, which is related to the regularity of the traveling waves.

Lemma 5.1

If $\varphi$ is a traveling wave of equation (4.1) and $\varphi \in H^1(\mathbb {R})$, then

$$\begin{aligned} \left( \varphi -\sigma +\frac{\beta _0}{\beta }\right) ^k\in C^j\left( \mathbb {R}{\setminus }\varphi ^{-1}\left( \sigma -\frac{\beta _0}{\beta }\right) \right) , \quad \mathrm {for}\quad k\ge 2^j. \end{aligned}$$

Furthermore, we conclude

$$\begin{aligned} \varphi \in C^{\infty }\left( \mathbb {R}{\setminus }\varphi ^{-1} \left( \sigma -\frac{\beta _0}{\beta }\right) \right) . \end{aligned}$$

Proof

Let $v=\varphi -\sigma +\frac{\beta _0}{\beta }$. Then Eq. (5.3) infers

$$\begin{aligned} (v^2)_{xx} = v_{x}^2 + \zeta (v), \end{aligned}$$

where $\zeta (v)$ is a polynomial in v, more precisely

$$\begin{aligned} \zeta (v)= & {} 2(c-\sigma )\left( v+\sigma -\frac{\beta _0}{\beta }\right) + 3\left( v+\sigma -\frac{\beta _0}{\beta }\right) ^2 + \frac{2\omega _1}{3\alpha ^2}\left( v+\sigma -\frac{\beta _0}{\beta }\right) ^3\\&+ \frac{\omega _2}{3\alpha ^3}\left( v+\sigma -\frac{\beta _0}{\beta }\right) ^4. \end{aligned}$$

From the assumption, we know $v\in H^1_{loc}(\mathbb {R})$, which gives rise to $v_x^2 + \zeta (v) \in L_{loc}^1(\mathbb {R})$ and $(v^2)_{xx}\in L_{loc}^1(\mathbb {R})$. Thus, $(v^2)_{x}\in W_{loc}^{1,1}(\mathbb {R})$. This implies that $(v^2)_{x}$ is absolutely continuous, and $v^2$, $v^3$ belongs to $C^1(\mathbb {R}{\setminus } v^{-1}(0))$. Moreover,

$$\begin{aligned} \begin{aligned} (v^k)_{xx} =\,&[(v^k)_x]_x = [kv^{k-1}v_x]_x \\ =\,&\left[ \frac{k}{2}v^{k-2}(2vv_x)\right] _x = \frac{k}{2}(v^{k-2})_x(v^2)_x + \frac{k}{2}v^{k-2}(v^2)_{xx} \\ = \,&k(k-2)v^{k-2}v_{x}^2 + \frac{k}{2} v^{k-2}[v_{x}^2 + \zeta (v)] = k\left( k-\frac{3}{2}\right) v^{k-2}v_{x}^2 + \frac{k}{2}v^{k-2} \zeta (v). \end{aligned} \end{aligned}$$

For $k=3$, the right-hand side of the above equation is in $L^1_{loc}(\mathbb {R})$. Therefore, we have

$$\begin{aligned} v^3\in C^1(\mathbb {R}){\setminus } v^{-1}(0)). \end{aligned}$$

Similarly, for $k\ge 4$, we obtain $(v^k)_{xx} = \frac{k}{4}(k-\frac{3}{2})v^{k-4}[(v^2)_x]^2 + \frac{k}{2}v^{k-2}\zeta (v)$. Since $v^2\in C^1(\mathbb {R}){\setminus } v^{-1}(0))$, it follows that

$$\begin{aligned} v^k\in C^2(\mathbb {R}){\setminus } v^{-1}(0)),\quad k\ge 4. \end{aligned}$$

For $k\ge 8$, we have $v^{k-2}\zeta (v)\in C^2(\mathbb {R}){\setminus } v^{-1}(0))$, by previous conclusion as well as $v^4, v^{k-4}\in C^2(\mathbb {R}){\setminus } v^{-1}(0))$. Since $v^{k-2}v_{x}^2=\frac{1}{4}(v^4)_x\frac{1}{k-4}(v^{k-4})_x\in C^1(\mathbb {R}){\setminus } v^{-1}(0))$, we have

$$\begin{aligned} v^k\in C^3(\mathbb {R}){\setminus } v^{-1}(0)), \quad k\ge 8. \end{aligned}$$

Extending these arguments to higher values of k, we prove that

$$\begin{aligned} v^k\in C^j(\mathbb {R}{\setminus } v^{-1}(0)), \quad \mathrm {for} \quad k\ge 2^j. \end{aligned}$$

This completes the proof of Lemma 5.1. $\square$

We may rewrite Eq. (5.2) by multiplying by $\varphi _{x}$ and integrating on $(-\infty ,x]$

$$\begin{aligned} (c-\sigma )\varphi ^2 + \varphi ^3 + \frac{\omega _1}{6\alpha ^2}\varphi ^4 + \frac{\omega _2}{10\alpha ^3}\varphi ^5 + \left( \sigma -\frac{\beta _0}{\beta }\right) \varphi _{x}^2 - \varphi \varphi _{x}^2 = 0, \end{aligned}$$

which implies, if $\varphi \ne \sigma -\frac{\beta _0}{\beta }$ for all x,

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2\left[ \frac{\omega _2}{10\alpha ^3}\varphi ^3 + \frac{\omega _1}{6\alpha ^2}\varphi ^2 + \varphi + (c-\sigma )\right] }{\varphi -\sigma +\frac{\beta _0}{\beta }} = \frac{\varphi ^2f(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }}:=F(\varphi ). \end{aligned}$$

(5.4)

Applying the similar arguments as introduced in Lenells (2005), we have the following conclusion.

• 1. When $\varphi$ approaches a simple zero m of $F(\varphi )$ so that $F(m)=0$ and $F'(m)\ne 0$, the solution $\varphi$ of (5.4) satisfies

  $$\begin{aligned} \varphi _x^2=(\varphi -m)F'(m) + O((\varphi -m)^2), ~\mathrm {as}~ \varphi \rightarrow m, \end{aligned}$$

  (5.5)

  where $f=O(g)$ as $x\rightarrow a$ means $|\frac{f(x)}{g(x)}|$ is bounded in some interval $[a-\varepsilon , a+\varepsilon ]$ with $\varepsilon >0$. Then, we have

  $$\begin{aligned} \varphi (x)=m+\frac{1}{4}(x-x_0)^2F'(m) + O((x-x_0)^4), ~\mathrm {as}~ x\rightarrow x_0, \end{aligned}$$

  (5.6)

  where $\varphi (x_0)=m$.

• 2. If $F(\varphi )$ has a double zero at $\varphi =0$ such that $F(0)=F'(0)=0$ and $F''(0)>0$, then

  $$\begin{aligned} \varphi _x^2=\varphi ^2F''(0) + O(\varphi ^3), ~\mathrm {as}~ \varphi \rightarrow 0. \end{aligned}$$

  (5.7)

  Hence,

  $$\begin{aligned} \varphi = O\Big (\exp (-\sqrt{F''(0)}|x|)\Big ), ~\mathrm {as}~ |x|\rightarrow \infty , \end{aligned}$$

  (5.8)

  which implies $\varphi \rightarrow 0$ exponentially as $x\rightarrow \infty$.

• 3. If $\varphi$ approaches a simple pole $\varphi (x_0)=\sigma -\frac{\beta _0}{\beta }$ of $F(\varphi )$, then

  $$\begin{aligned}&\varphi (x) - \sigma +\frac{\beta _0}{\beta } = \lambda |x-x_0|^{2/3} + O((x-x_0)^{4/3}), \quad \mathrm {as}\quad x\rightarrow x_0, \end{aligned}$$

  (5.9)
  $$\begin{aligned}&\varphi _x= {\left\{ \begin{array}{ll} \frac{2}{3}\lambda |x-x_0|^{-1/3} + O((x-x_0)^{1/3}), \quad \mathrm {as}\quad x\downarrow x_0, \\ - \frac{2}{3}\lambda |x-x_0|^{-1/3} + O((x-x_0)^{1/3}), \quad \mathrm {as}\quad x\uparrow x_0, \end{array}\right. } \end{aligned}$$

  (5.10)

  for some constant $\lambda$.

• 4. Peaked traveling waves occur when $\varphi$ suddenly changes direction: $\varphi _x\mapsto -\varphi _x$ according to Eq. (5.4).

Based on discussion above on traveling wave solution of Eq. (4.1), we will classify the various traveling wave solutions to (5.4).

In view of the expression of the function of f,  one should consider the following three different cases.

$$\begin{aligned} \sqrt{\frac{\sqrt{19}-4}{3}}<c<\frac{1}{\sqrt{8}},\quad \frac{1}{\sqrt{8}}<c<1 \quad \mathrm {and}\quad c=\frac{1}{\sqrt{8}}, \end{aligned}$$

corresponding to $\omega _2<0$, $\omega _2>0$ and $\omega _2=0$, respectively.

Let us start with

$$\begin{aligned} f(\varphi )=a_3\varphi ^3+a_2\varphi ^2+a_1\varphi +a_0, \quad a_3\ne 0, \end{aligned}$$

where

$$\begin{aligned} a_3=\frac{\omega _2}{10\alpha ^3},\quad a_2=\frac{\omega _1}{6\alpha ^2},\quad a_1=1,\quad a_0=c-\sigma . \end{aligned}$$

Define that $\eta =\varphi +\frac{a_2}{3a_3},$ that is, $\displaystyle \varphi =\eta -\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}.$ Then, by the property of cubic polynomial (Bronshtein et al. 2007), we can rewrite

$$\begin{aligned} f(\varphi )=f(\eta )=\frac{\omega _2}{10\alpha ^3}(\eta ^3+3\varrho \eta +2\kappa ), \end{aligned}$$

(5.11)

where

$$\begin{aligned} \varrho&= \frac{3a_3a_1-a_2^2}{9a_3^2} = \frac{10}{3}\frac{\alpha ^3}{\omega _2} - \frac{25}{81}\frac{\alpha ^2\omega _1^2}{\omega _2^2}, \end{aligned}$$

(5.12)

$$\begin{aligned} \kappa&= \frac{2a_2^3-9a_3a_2a_1+27a_3^2a_0}{54a_3^3} = \frac{125}{729}\frac{\alpha ^3\omega _1^3}{\omega _2^3} - \frac{25}{9}\frac{\alpha ^4\omega _1}{\omega _2^2} + 5(c-\sigma )\frac{\alpha ^3}{\omega _2}. \end{aligned}$$

(5.13)

The determinator of equation $f(\eta )=0$ is defined by

$$\begin{aligned} \begin{aligned} D =\,&\; \kappa ^2+\varrho ^3 = \frac{1000}{27}\frac{\alpha ^9}{\omega _2^3}-\frac{625}{243}\frac{\alpha ^8\omega _1^2}{\omega _2^4}-\frac{250}{9}(c-\sigma )\frac{\alpha ^7\omega _1}{\omega _2^3} \\&\; +\frac{1250}{729}(c-\sigma )\frac{\alpha ^6\omega _1^3}{\omega _2^4}+25(c-\sigma )^2\frac{\alpha ^6}{\omega _2^2}. \end{aligned} \end{aligned}$$

(5.14)

Case I:$\sqrt{\frac{\sqrt{19}-4}{3}}<c<\frac{1}{\sqrt{8}}.$ The restriction on c then yields that

$$\begin{aligned} \alpha>0,\quad \beta _0<0,\quad \beta>0,\quad \omega _1<0,\quad \omega _2>0. \end{aligned}$$

Consider $D=0$ as a quadratic equation of $c-\sigma$, that is

$$\begin{aligned} A(c-\sigma )^2 + B(c-\sigma ) + C = 0, \end{aligned}$$

(5.15)

where

$$\begin{aligned} A = \frac{25\alpha ^6}{\omega _2^2},\quad B = \frac{1250}{729}\frac{\alpha ^6\omega _1^3}{\omega _2^4}-\frac{250}{9}\frac{\alpha ^7\omega _1}{\omega _2^3}, \quad \mathrm{and} \; C = \frac{1000}{27}\frac{\alpha ^9}{\omega _2^3}-\frac{625}{243}\frac{\alpha ^8\omega _1^2}{\omega _2^4}. \end{aligned}$$

It is observed from $c\in (\sqrt{\frac{\sqrt{19}-4}{3}},\frac{1}{\sqrt{8}})$ that $8-139c^2<0$ and $8c^2-1<0$. This then implies that

$$\begin{aligned} B = \frac{250}{9}\frac{\alpha ^6\omega _1}{\omega _2^3}\frac{c^2(8-139c^2)}{18(c^2+1)(8c^2-1)} < 0. \end{aligned}$$

For C, it is easy to see that

$$\begin{aligned} C = \frac{125}{27}\frac{\alpha ^8}{\omega _2^3}\frac{(128c^4-21c^2+10)}{2(c^2+1)(8c^2-1)} < 0. \end{aligned}$$

Hence, the quadratic equation $D=0$ has a negative solution $y_1$ and a positive solution $y_2$, where

$$\begin{aligned} \begin{aligned} y_{1}&= \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\frac{25}{729}\frac{\omega _1^3}{\omega _2^2} - \frac{1}{2}\sqrt{\Delta } < 0, \\ y_{2}&= \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\frac{25}{729}\frac{\omega _1^3}{\omega _2^2} + \frac{1}{2}\sqrt{\Delta }> 0, ~\mathrm {and }\\ \Delta&= \left( \frac{50}{729}\frac{\omega _1^3}{\omega _2^2}-\frac{10}{9}\frac{\alpha \omega _1}{\omega _2}\right) ^2 -4\left( \frac{40}{27}\frac{\alpha ^3}{\omega _2}-\frac{25}{243}\frac{\alpha ^2\omega _1^2}{\omega _2^2}\right) >0. \end{aligned} \end{aligned}$$

In addition, we know

• 1. If $y_1<c-\sigma <y_2$, then $D<0$;

• 2. If $c-\sigma =y_1$ or $c-\sigma =y_2$, then $D=0$;

• 3. If $c-\sigma <y_1$ or $c-\sigma >y_2$, then $D>0$.

The following theorem provides the classification of traveling wave solution to Eq. (4.1) when $D>0$ and $\sqrt{\frac{\sqrt{19}-4}{3}}<c<\frac{1}{\sqrt{8}}$, i.e., $f(\varphi )$ has exactly one real root, which takes the form of $\eta _1=\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}+\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}$.

Theorem 5.1

Assume that $\sqrt{\frac{\sqrt{19}-4}{3}}<c<\frac{1}{\sqrt{8}}$.

(1) Suppose $\sigma >c-y_1$.

• If $\sigma - \frac{\beta _0}{\beta } = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is a peaked traveling wave solution $\varphi >0$

  with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

• If $\sigma - \frac{\beta _0}{\beta } > \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is a smooth traveling wave solution $\varphi >0$

  with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

• If $\sigma - \frac{\beta _0}{\beta } < \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is a cusped traveling wave solution $\varphi >0$

  with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

(2) Suppose $\sigma <\min \{ \frac{\beta _0}{\beta },c-y_2 \}$ and $\gamma _2=\frac{\omega _2}{10\alpha ^3}(\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1)>0$.

• If $\sigma - \frac{\beta _0}{\beta } = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is an antipeaked traveling wave solution $\varphi <0$

  with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

• If $\sigma - \frac{\beta _0}{\beta } < \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is a smooth traveling wave solution $\varphi <0$

  with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

• If $\sigma - \frac{\beta _0}{\beta } > \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then there is an anticusped traveling wave solution $\varphi <0$

  with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

Proof

Since $\frac{\beta _0}{\beta } = \frac{c(c^4+6c^2-1)}{3c^4+8c^2-1}$, this implies $c-\frac{\beta _0}{\beta }=\frac{2c^3(c^2+1)}{3c^4+8c^2-1}>0$, for $c\in (\sqrt{\frac{\sqrt{19}-4}{3}},\frac{1}{\sqrt{8}})$. The decay of $\varphi (x)$ at infinity gives a necessary condition for the existence of traveling wave which is

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\frac{\frac{\omega _2}{10\alpha ^3}\varphi ^3 + \frac{\omega _1}{6\alpha ^2}\varphi ^2 + \varphi + (c-\sigma )}{\varphi -\sigma +\frac{\beta _0}{\beta }}\ge 0, \end{aligned}$$

which implies

$$\begin{aligned} \left\{ { \begin{array}{l} {c - \sigma \ge 0,}\\ {\frac{\beta _0}{\beta }-\sigma > 0,} \end{array}} \right. \quad \mathrm {or}\quad \left\{ { \begin{array}{l} {c - \sigma \le 0,}\\ {\frac{\beta _0}{\beta }-\sigma < 0,} \end{array}} \right. \end{aligned}$$

i.e., $\sigma <\frac{\beta _0}{\beta }$ or $\sigma \ge c$ (when $\sigma =c$, $D<0$).

By the property of cubic equation, it is thereby inferred from $D>0$ that $f=0$ has one real root and two complex roots. Based on necessary condition for the existence of traveling wave, we will discuss the following two cases for $D>0$: $\quad \sigma > c$ and $\sigma < \frac{\beta _0}{\beta }.$

If $\sigma > c$, then

$$\begin{aligned} \begin{aligned} \varrho&= \frac{10}{3}\frac{\alpha ^3}{\omega _2} - \frac{25}{81}\frac{\alpha ^2\omega _1^2}{\omega _2^2} = \frac{5}{3}\frac{\alpha ^2c^2}{\omega _2}\left[ \frac{(91c^2-2)}{6(c^2+1)(8c^2-1)} \right]< 0,\\ \kappa&= \frac{125}{729}\frac{\alpha ^3\omega _1^3}{\omega _2^3} - \frac{25}{9}\frac{\alpha ^4\omega _1}{\omega _2^2} + 5\left( c-\sigma \frac{\alpha ^3}{\omega _2}\right) \\&= \frac{25}{9}\frac{\alpha ^3\omega _1}{\omega _2^2}\left[ \frac{c^2(8-139c^2)}{18(c^2+1)(8c^2-1)} \right] + 5(c-\sigma )\frac{\alpha ^3}{\omega _2} <0, \end{aligned} \end{aligned}$$

where $\omega _1<0$, $\omega _2>0$, $c-\sigma <0$, $8c^2-1<0$, $91c^2-2>0$ and $8-139c^2<0$, since $c\in (\sqrt{\frac{\sqrt{19}-4}{3}},\frac{1}{\sqrt{8}})$.

It then follows from the Cardano formula that the real root of $f(\eta )=0$ can be expressed as

$$\begin{aligned} \eta _1=\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}+\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}. \end{aligned}$$

(5.16)

Denote $u=\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}$ and $v=\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}$. Then the other two roots can be expressed as

$$\begin{aligned} \eta _2 =\,&u\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i\right) +v\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i\right) ,\\ \eta _3 =\,&u\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i\right) +v\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i\right) . \end{aligned}$$

Hence,

$$\begin{aligned} f(\eta ) = \frac{\omega _2}{10\alpha ^3} (\eta -\eta _1)(\eta -\eta _2)(\eta -\eta _3), \end{aligned}$$

where $\eta _1>0$ and $(\eta -\eta _2)(\eta -\eta _3)>0.$ Substituting $\eta$ by $\varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ implies

$$\begin{aligned} f(\varphi ) = \frac{\omega _2}{10\alpha ^3} \left( \varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1\right) \left( \varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _2\right) \left( \varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _3\right) , \end{aligned}$$

where $\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}>0$ and $(\varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _2)(\varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _3)>0$.

Let

$$\begin{aligned} \gamma _1=\frac{\omega _2}{10\alpha ^3} \left( \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1\right) <0, \end{aligned}$$

(5.17)

and

$$\begin{aligned} Q(\varphi )=\left( \varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _2\right) \left( \varphi +\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _3\right) . \end{aligned}$$

(5.18)

Then Eq. (5.4) can be written as the following form

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\frac{\omega _2}{10\alpha ^3}\varphi +\gamma _1)Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} = \frac{\frac{\omega _2}{10\alpha ^3}\varphi ^2\left[ \varphi - (\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}) \right] Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} :=G_1(\varphi ). \end{aligned}$$

Hence, if $\sigma - \frac{\beta _0}{\beta } = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $\varphi$ suddenly changes direction from $\varphi _x$ to $-\varphi _x$ at $\varphi =\sigma -\frac{\beta _0}{\beta }$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$, which give rise to the existence of a peaked traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

If $\sigma - \frac{\beta _0}{\beta } > \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $G_1(\varphi )$ has a simple zero at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. In view of (5.5)–(5.8), there exists a smooth traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

If $\sigma - \frac{\beta _0}{\beta } < \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $G_1(\varphi )$ has a pole at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. It then implies from (5.7)–(5.10) that there exists a cusped traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

In the case of $\sigma < \frac{\beta _0}{\beta }$, it is inferred from Eq. (5.11) that $r<0$. From the property of $\varphi$ decaying at infinity, we require $\frac{\omega _2}{10\alpha ^3}\cdot q = c-\sigma >0$, which implies $q>0$. Equation (5.4) then can be written as

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\frac{\omega _2}{10\alpha ^3}\varphi +\gamma _2)Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} = \frac{\frac{\omega _2}{10\alpha ^3}\varphi ^2\left[ \varphi - (\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}) \right] Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} :=G_2(\varphi ), \end{aligned}$$

where $\gamma _2=\frac{\omega _2}{10\alpha ^3}(\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1)>0$, $\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}<0$, and $\eta _1<0$ in this case.

Hence, if $\sigma - \frac{\beta _0}{\beta } = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $\varphi$ suddenly changes direction from $\varphi _x$ to $-\varphi _x$ at $\varphi =\sigma -\frac{\beta _0}{\beta }$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$, which gives rise to the existence of an antipeaked traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$.

If $\sigma - \frac{\beta _0}{\beta } < \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $G_1(\varphi )$ has a simple zero at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. In view of (5.5)–(5.8), there exists a smooth traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

If $\sigma - \frac{\beta _0}{\beta } > \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then $G_1(\varphi )$ has a pole at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. It is then deduced from (5.7)–(5.10) that these is $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$. This completes the proof of Theorem 5.1. $\square$

Remark 5.1

Since the existence of peaked traveling wave solution requires $\sigma >c-y_1$ and $\sigma = \frac{\beta _0}{\beta } + \eta _1(\sigma ) - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ in Case (1). Due to $c>\frac{\beta _0}{\beta }$, which implies $\sigma < c + \eta _1(\sigma ) - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$, then the necessary condition becomes $c + \eta _1(\sigma ) - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2} > c - y_1$. As $\eta _1$ is positive, the above condition can be simplified as $\displaystyle y_1 > \frac{5}{9}\frac{\alpha \omega _1}{\omega _2},$ where $y_1 = \frac{5}{9}\frac{\alpha \omega _1}{\omega _2} - \frac{25}{729}\frac{\omega _1^3}{\omega _2^2}-\frac{1}{2}\sqrt{\Delta }.$ This requires

$$\begin{aligned} 0< \Delta < \left( \frac{- 50}{729}\frac{\omega _1^3}{\omega _2^2}\right) ^2. \end{aligned}$$

(5.19)

Actually,

$$\begin{aligned} \frac{50}{729}\frac{\omega _1^3}{\omega _2^2} =\,&-\frac{50}{54}\frac{c^3(c^2-2)(c^2+1)}{(c^2-1)(8c^2-1)^2}, \end{aligned}$$

(5.20)

$$\begin{aligned} \Delta =\,&\left( -\frac{50}{54}\frac{c^3(c^2-2)(c^2+1)}{(c^2-1)(8c^2-1)^2} + \frac{10}{3}\frac{c^3(c^2+1)}{(c^2-1)(8c^2-1)}\right) ^2 \nonumber \\&-4\left( \frac{80}{27}\frac{c^6(c^2+1)}{(c^2-2)(c^2-1)^2(8c^2-1)}-\frac{25}{27}\frac{c^6(c^2_1)^2}{(c^2-1)^2(8c^2-1)^2}\right) . \end{aligned}$$

(5.21)

The leading order of $\Delta -\left( \frac{50}{729}\frac{\omega _1^3}{\omega _2^2}\right) ^2$ is $(8c^2-1)^3$, and it has the following form

$$\begin{aligned} -\frac{500}{162}\frac{c^6(c^2-2)(c^2+1)^2}{(c^2-1)^2(8c^2-1)^3} < 0, \quad \mathrm {when}\quad c \rightarrow \frac{1}{\sqrt{8}}^-, \end{aligned}$$

which implies (5.19) holds. This guarantees the existence of peaked traveling wave solution.

Case II:$\frac{1}{\sqrt{8}}<c\le 1$. It is observed that the restriction on c gives that $\alpha>0,\quad \beta _0<0,\quad \beta >0,\quad \omega _1<0,$ and $\omega _2<0.$ In this case, Eq. (5.15) has a negative solution $y_1$ and a positive solution $y_2$. We could follow the similar proof in Theorem 5.1 to obtain the following results.

Theorem 5.2

Assume $\frac{1}{\sqrt{8}}<c\le 1$.

• (1) If $\sigma >c-y_1$, then there is a smooth traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi =-\frac{10\alpha ^3}{\omega _2}\gamma _3$ where $\gamma _3=\frac{\omega _2}{10\alpha ^3}\Big (\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}-\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}\Big )$ and a cusped traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi =\sigma - \frac{\beta _0}{\beta }$.

• (2) If $\sigma <\min \{\frac{\beta _0}{\beta },c-y_2\}$ and $\gamma _4>0$, then there is a smooth traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi =-\frac{10\alpha ^3}{\omega _2}\gamma _4$, where $\gamma _4=\frac{\omega _2}{10\alpha ^3}\Big (\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}+\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}\Big )$ and an anticusped traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi =\sigma - \frac{\beta _0}{\beta }$.

Proof

According to the decay of $\varphi (x)$ at infinity, a necessary condition for the existence of traveling wave is that $\sigma \ge c$ or $\sigma <\frac{\beta _0}{\beta }$, since $c>\frac{\beta _0}{\beta }$ for $\frac{1}{\sqrt{8}}<c\le 1$. Note that $\sigma =c$ is not included since $D<0$ when $\sigma =c$.

Case (1). If $\sigma >c$, we know $p<0$ and $q>0$ from (5.12) and (5.13). Then Eq. (5.4) has the following form

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\frac{\omega _2}{10\alpha ^3}\varphi +\gamma _3)Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} = \frac{\frac{\omega _2}{10\alpha ^3}\varphi ^2\left[ \varphi - (\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}) \right] Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} :=G_3(\varphi ), \end{aligned}$$

where $\gamma _3=\frac{\omega _2}{10\alpha ^3}(\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1)<0$, $\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}<0$, and $\eta _1<0$ in this case.

Hence, for $\varphi <0$, $G_3(\varphi )$ has a simple zero at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. According to (5.5), (5.6), (5.7), (5.8), there is a smooth traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

For $\varphi >0$, $G_3(\varphi )$ has a pole at $\varphi =\sigma -\frac{\beta _0}{\beta }$ and a double zero at $\varphi =0$. From (5.7)–(5.10), there is a cusped traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi = \sigma -\frac{\beta _0}{\beta }$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

Case (2). If $\sigma <\frac{\beta _0}{\beta }$, then we know $p<0$ in (5.12). It then follows from the property of $\varphi$ decaying at infinity that

$$\begin{aligned} \kappa <0 ~\mathrm {and}~ \frac{\omega _2}{10\alpha ^3}\Big (\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\root 3 \of {-\kappa +\sqrt{\kappa ^2+\varrho ^3}}-\root 3 \of {-\kappa -\sqrt{\kappa ^2+\varrho ^3}}\Big )>0. \end{aligned}$$

Similar to Case (1), we have

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\frac{\omega _2}{10\alpha ^3}\varphi +\gamma _4)Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} = \frac{\frac{\omega _2}{10\alpha ^3}\varphi ^2\left[ \varphi - (\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}) \right] Q(\varphi )}{\varphi -\sigma +\frac{\beta _0}{\beta }} :=G_4(\varphi ), \end{aligned}$$

where $\gamma _4=\frac{\omega _2}{10\alpha ^3}(\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}-\eta _1)<0$, $\eta _1-\frac{5}{9}\frac{\alpha \omega _1}{\omega _2}>0$, and $\eta _1>0$ in this case.

Consequently, for $\varphi >0$, $G_4(\varphi )$ has a simple zero at $\varphi =\eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and a double zero at $\varphi =0$. From (5.5)–(5.8), there is a smooth traveling wave solution $\varphi >0$ with $\max \limits _{x\in {\mathbb {R}}}\varphi = \eta _1 - \frac{5}{9}\frac{\alpha \omega _1}{\omega _2}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

For $\varphi <0$, $G_4(\varphi )$ has a pole at $\varphi =\sigma -\frac{\beta _0}{\beta }$ and a double zero at $\varphi =0$. It is then deduced from (5.7)–(5.10) there is a cusped traveling wave solution $\varphi <0$ with $\min \limits _{x\in {\mathbb {R}}}\varphi = \sigma -\frac{\beta _0}{\beta }$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$. This completes the proof of Theorem 5.2. $\square$

Case III:$c = \frac{1}{\sqrt{8}}.$ In this case, we have

$$\begin{aligned} \alpha = \frac{1}{9},\quad \beta _0 = -\frac{5\sqrt{2}}{648},\quad \beta = \frac{1}{162},\quad \omega _1 = -\frac{35\sqrt{2}}{81},\quad \omega _2 = 0, \end{aligned}$$

which implies

$$\begin{aligned} \frac{\omega _1}{6\alpha ^2} = -\frac{35\sqrt{2}}{6}, \quad c= \frac{\sqrt{2}}{4}, \quad \frac{\beta _0}{\beta } = -\frac{5\sqrt{2}}{4}. \end{aligned}$$

Hence, Eq. (5.4) can be simplified as

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2\left[ \varphi ^2-\frac{3\sqrt{2}}{35}\varphi -\frac{3\sqrt{2}}{35} (\frac{\sqrt{2}}{4}-\sigma )\right] }{\frac{3\sqrt{2}}{35}\left[ (\sigma +\frac{5\sqrt{2}}{4})-\varphi \right] }, \end{aligned}$$

(5.22)

where $f(\varphi ) = \varphi ^2-\frac{3\sqrt{2}}{35}\varphi -\frac{3\sqrt{2}}{35}(\frac{\sqrt{2}}{4}-\sigma )$. The following discussion enlists all possible distribution of the roots of f.

• (a) $f(\varphi )$ has no zeros: If $\sigma > \frac{19\sqrt{2}}{70}$, then $(\frac{3\sqrt{2}}{35})^2+4\cdot \frac{3\sqrt{2}}{35}\cdot (\frac{\sqrt{2}}{4}-\sigma ) < 0$. Hence, $f(\varphi )>0.$

• (b) $f(\varphi )$ has a double zero: If $\sigma = \frac{19\sqrt{2}}{70}$, then $(\frac{3\sqrt{2}}{35})^2+4\cdot \frac{3\sqrt{2}}{35}\cdot (\frac{\sqrt{2}}{4}-\sigma ) = 0$. Hence, $f(\varphi ) = (\varphi - \frac{3\sqrt{2}}{70})^2.$

• (c) $f(\varphi )$ has two simple zeros: If $\sigma < \frac{19\sqrt{2}}{70}$, then $(\frac{3\sqrt{2}}{35})^2+4\cdot \frac{3\sqrt{2}}{35}\cdot (\frac{\sqrt{2}}{4}-\sigma ) > 0$. Hence, $f(\varphi ) = (\varphi -M_1)(\varphi -M_2),$ where

  $$\begin{aligned} M_1= & {} \frac{3\sqrt{2}}{70} - \frac{1}{2}\sqrt{\Big (\frac{3\sqrt{2}}{35}\Big )^2 + 4\cdot \frac{3\sqrt{2}}{35} \cdot \Big (\frac{\sqrt{2}}{4} - \sigma \Big )},\\ M_2= & {} \frac{3\sqrt{2}}{70} + \frac{1}{2}\sqrt{\Big (\frac{3\sqrt{2}}{35}\Big )^2 + 4\cdot \frac{3\sqrt{2}}{35} \cdot \Big (\frac{\sqrt{2}}{4} - \sigma \Big )}, \end{aligned}$$

  and $M_1 < M_2$, $M_1+M_2>0.$ In addition, if $\sigma >\frac{\sqrt{2}}{4}$, then $M_1M_2>0$; if $\sigma =\frac{\sqrt{2}}{4}$, then $M_1 = 0$, $M_2 = \frac{3\sqrt{2}}{35}$; if $\sigma <\frac{\sqrt{2}}{4}$, then $M_1M_2<0$.

In view of Eq. (5.22), it is found from decay of $\varphi$ at infinity that a necessary condition for the existence of traveling wave solution is

$$\begin{aligned} \lim _{|x|\rightarrow \infty } \frac{\varphi ^2-\frac{3\sqrt{2}}{35}\varphi -\frac{3\sqrt{2}}{35}\left( \frac{\sqrt{2}}{4}-\sigma \right) }{\left( \sigma +\frac{5\sqrt{2}}{4}\right) -\varphi } \ge 0, \end{aligned}$$

which implies $\sigma <-\frac{5\sqrt{2}}{4}$ or $\sigma \ge \frac{\sqrt{2}}{4}$.

With the results established above, we are in the position to classify all traveling waves of equation (4.1) when $\omega _2 = 0$ for various $\sigma$.

Theorem 5.3

Let $c = \frac{1}{\sqrt{8}}$.

• 1. If $\sigma < -\frac{5\sqrt{2}}{4}$, i.e., $f(\varphi )$ has a negative root and a positive root, then:

• 1a. If $\sigma +\frac{5\sqrt{2}}{4}< M_1 < 0$, then there is a smooth traveling wave solution $\varphi > 0$ with $\max \limits _{x\in \mathbb {R}} \varphi (x)= M_2$;

• 1b. If $M_1< \sigma +\frac{5\sqrt{2}}{4} < 0$, then there is an anticusped traveling wave solution $\varphi < 0$ with $\min \limits _{x\in \mathbb {R}}\varphi (x) = \sigma + \frac{5\sqrt{2}}{4}$;

• 1c. If $\sigma +\frac{5\sqrt{2}}{4} = M_1$, then there is an antipeaked traveling wave solution $\varphi < 0$ with $\min \limits _{x\in \mathbb {R}}\varphi (x) = M_1 = \sigma + \frac{5\sqrt{2}}{4}$.

• 2. If $\sigma = \frac{\sqrt{2}}{4}$, i.e., $f(\varphi )$ has two simple roots: $M_1 = 0$, $M_2 = \frac{3\sqrt{2}}{35}$, there is no traveling wave solution.

• 3. If $\frac{\sqrt{2}}{4}< \sigma < \frac{19\sqrt{2}}{70}$, i.e., $f(\varphi )$ has two simple roots: $M_1> M_2 > 0$, $M_2 = \frac{3\sqrt{2}}{35}$, then there is a smooth traveling wave $\varphi > 0$ with $\max \limits _{x\in \mathbb {R}}\varphi (x) = M_1$.

• 4. If $\sigma = \frac{19\sqrt{2}}{70}$, i.e., $f(\varphi )$ has a double roots: $M_1 = M_2 = \frac{3\sqrt{2}}{70}$, then there is a smooth traveling wave $\varphi > 0$ with $\max \limits _{x\in \mathbb {R}}\varphi (x) = M_1=M_2$ and a cusped traveling wave solution $\varphi > 0$ with $\max \limits _{x\in \mathbb {R}}\varphi (x) = \frac{213\sqrt{2}}{140}$.

• 5. If $\sigma > \frac{19\sqrt{2}}{70}$, i.e., $f(\varphi ) > 0$ for all $\varphi (x)\in \mathbb {R}$, then there is a cusped traveling wave solution $\varphi >0$ with $\max \limits _{x\in \mathbb {R}}\varphi (x) = \sigma + \frac{5\sqrt{2}}{4}$.

Proof

Case (1), If $\sigma < -\frac{5\sqrt{2}}{4}$, then $f(\varphi )$ has two simple roots $M_1$ and $M_2$ satisfying $M_2>0>M_1$, which implies

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\varphi -M_1)(\varphi -M_2)}{\frac{3\sqrt{2}}{35}\left[ (\sigma +\frac{5\sqrt{2}}{4})-\varphi \right] } := F_1(\varphi ), \quad \mathrm {where}\quad \sigma +\frac{5\sqrt{2}}{4} < 0. \end{aligned}$$

(5.23)

From (5.23) we know that $\varphi$ can not oscillate around zero near infinity. Let us consider the following two cases.

(1.1) $\varphi (x)>0$ near $-\infty$. Then there is some $x_0$ sufficiently large negative so that $\varphi (x_0) = \varepsilon > 0$, with $\varepsilon$ sufficiently small, and $\varphi _x(x_0)>0$. Since $\sqrt{F_1(\varphi )}$ is locally Lipschitz in $\varphi$ for $\varphi >0$. Hence, there is a local solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi _x = \sqrt{F_1(\varphi )}, \\ \varphi (x_0) = \varepsilon . \\ \end{array}\right. } \end{aligned}$$

on $[x_0-L, x_0+L]$ for some $L>0$. Therefore from (5.5), (5.6), (5.7) and (5.8) we see that in this case we can obtain a smooth traveling wave solution with maximum height $\varphi = M_2$ and an exponential decay to zero at infinity

$$\begin{aligned} \varphi (x) = O\left( \exp \left( -\sqrt{\frac{\frac{3\sqrt{2}}{35}(\frac{\sqrt{2}}{4}-\sigma )}{\sigma +\frac{5\sqrt{2}}{4}}}\Big |x\Big |\right) \right) \quad \mathrm {as}\quad |x|\rightarrow \infty . \end{aligned}$$

(5.24)

(1.2) $\varphi (x)<0$ near $-\infty$. Then there is some $x_0$ sufficiently large negative so that $\varphi (x_0) = - \varepsilon < 0$, with $\varepsilon$ sufficiently small, and $\varphi _x(x_0)<0$. Since $\sqrt{F_1(\varphi )}$ is locally Lipschitz in $\varphi$ for $\sigma +\frac{5\sqrt{2}}{4}<\varphi <0$, we an continue the local solution to $(-\infty , x_0-L]$ with $\varphi (x)\rightarrow 0$ as $x\rightarrow -\infty$. As for $x\ge x_0+L$, we can solve the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi _x = - \sqrt{F_1(\varphi )}, \\ \varphi (x_0) = - \varepsilon . \\ \end{array}\right. } \end{aligned}$$

If $M_1< \sigma + \frac{5\sqrt{2}}{4} < 0$, the initial value problem can be solved all the way until $\varphi =\sigma +\frac{5\sqrt{2}}{4}$, which is a simple pole of $F_1(\varphi )$. From (5.7), (5.8), (5.9) and (5.10) we know that we can construct an anticusped solution with a cusp singularity at $\varphi = \sigma + \frac{5\sqrt{2}}{4}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$; if $M_1 = \sigma + \frac{5\sqrt{2}}{4} < 0$, then $\varphi$ suddenly changes direction from $\varphi _x$ to $-\varphi _x$ at $\varphi =M_1 = \sigma + \frac{5\sqrt{2}}{4}$, which implies the existence of an antipeaked solution $\varphi < 0$ with $\min \limits _{x\in \mathbb {R}}\varphi (x) = M_1 = \sigma + \frac{5\sqrt{2}}{4}$ and $\varphi \rightarrow 0$ exponentially as $|x|\rightarrow \infty$.

Case (2), If $\sigma = \frac{\sqrt{2}}{4}$, then $f(\varphi )$ has two simple roots $M_1=0$ and $M_2=\frac{3\sqrt{2}}{35}$, which implies

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^3\left( \varphi -\frac{3\sqrt{2}}{35}\right) }{\frac{3\sqrt{2}}{35}\left[ \frac{3\sqrt{2}}{2}-\varphi \right] } := F_2(\varphi ). \end{aligned}$$

(5.25)

Notice that $\varphi (x)<0$ near $-\infty$. Because $\varphi (x)\rightarrow 0$ as $x\rightarrow -\infty$, there is some $x_0$ sufficiently negative so that $\varphi (x_0) = -\varepsilon <0$ with $\varepsilon >0$ sufficiently small, and $\varphi _{x}(x_0)<0$. From standard ODE theory, we can generate a unique local solution $\varphi (x)$ on $[x_0-L, x_0+L]$ for some $L>0$. Due to

$$\begin{aligned} F_2'(\varphi ) = \frac{\varphi ^2\left[ -3\varphi ^2+\frac{216\sqrt{2}}{35}\varphi - \frac{27}{35}\right] }{\frac{3\sqrt{2}}{35}\left( \frac{3\sqrt{2}}{2}-\varphi \right) ^2}< 0, \quad \mathrm {for}\quad \varphi <0, \end{aligned}$$

we know $F_2(\varphi )$ decreases for $\varphi <0$. Since $\varphi _{x}(x_0)<0$, $\varphi$ decreases near $x_0$, which implies $F_2(\varphi )$ increases near $x_0$. Hence, by $F'_2(\varphi )$, $\varphi _x$ decreases near $x_0$, and then $\varphi$ and $\varphi _x$ both decrease on $[x_0-L, x_0+L]$. Since $\sqrt{F_1(\varphi )}$ is locally Lipschitz in $\varphi$ for $\varphi <0$, we can continue the local solution to all $\mathbb {R}$ and obtain that $\varphi (x)\rightarrow -\infty$ as $x\rightarrow \infty$, which fails to be in $H^1$. Thus, there is no traveling wave solution in this case.

Case (3), If $\frac{\sqrt{2}}{4}<\sigma <\frac{19\sqrt{2}}{70}$, then $f(\varphi )$ has two simple roots $M_2$ and $M_1$, which implies

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2(\varphi -M_1)(\varphi -M_2)}{\frac{3\sqrt{2}}{35}\left[ \left( \sigma +\frac{5\sqrt{2}}{4}\right) -\varphi \right] } := F_3(\varphi ), \quad \mathrm {where}\quad 0<M_1<M_2<\sigma +\frac{5\sqrt{2}}{4}. \end{aligned}$$

(5.26)

Similar to Case (1), we know that $\varphi$ can not be oscillated around zero near infinity. Let us consider the following two cases.

(3.1) $\varphi (x)>0$ near $-\infty$. Then the same analysis as used in the proof of Case (1.1) leads to the conclusion that there is a smooth traveling wave solution with maximum height $\varphi = M_1$ and an exponential decay to zero at infinity.

(3.2) $\varphi (x)<0$ near $-\infty$. A direct computation shows that $F'_3(\varphi )<0$, if $\varphi <0$, where

$$\begin{aligned} F_3'(\varphi ) = \frac{\left[ 4\varphi ^3-3(M_1+M_2)\varphi ^2+2M_1M_2\varphi \right] \left( \sigma +\frac{5\sqrt{2}}{4}\right) -3\varphi ^4+2(M_1+M_2)\varphi ^3-2M_1M_2\varphi ^2}{\left( \frac{3\sqrt{2}}{35}\right) ^2\left[ \left( \sigma +\frac{5\sqrt{2}}{4}-\varphi \right) \right] ^2}. \end{aligned}$$

Arguing as Case (2), there is no traveling wave solution in this case.

Case (4), If $\sigma = \frac{19\sqrt{2}}{70}$, then $f(\varphi )$ has a double root $M_1=M_2=\frac{3\sqrt{2}}{70}$, which implies

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2\left( \varphi -\frac{3\sqrt{2}}{70}\right) ^2}{\frac{3\sqrt{2}}{35}\left[ \frac{213\sqrt{2}}{140}-\varphi \right] } := F_4(\varphi ). \end{aligned}$$

(5.27)

(4.1) $\varphi (x)>0$ near $-\infty$. By the standard ODE theory in Case (1), if $\varphi$ reaches its absolutely maximum at $\varphi =M_1=M_2$, then there exists a smooth traveling wave solution with maximum height $\varphi = M_1=M_2$ and an exponential decay to zero at infinity; if $\varphi =M_1=M_2$ is not an absolutely maximum, then we obtain a cusped traveling wave solution with maximum height $\varphi = \frac{213\sqrt{2}}{140}$.

(4.2) $\varphi (x)<0$ near $-\infty$. From

$$\begin{aligned} F_4'(\varphi ) = \frac{\Big (-3\varphi ^3 +\frac{876\sqrt{2}}{140}\varphi ^2-\frac{3582}{4900}\varphi +\frac{7668\sqrt{2}}{686000} \Big )\varphi }{\frac{3\sqrt{2}}{35}\left( \frac{213\sqrt{2}}{140}-\varphi \right) ^2}, \end{aligned}$$

one can check that $F'_5(\varphi )<0$ for $\varphi <0$. Hence, similar to Case (2), there is no traveling wave solution in this case.

Case (5), If $\sigma > \frac{19\sqrt{2}}{70}$, then there is no real roots for $f(\varphi )$ and we know $f(\varphi )>0$ for all $\varphi (x)\in \mathbb {R}$. Denote

$$\begin{aligned} \varphi _x^2 = \frac{\varphi ^2f(\varphi )}{\frac{3\sqrt{2}}{35} \left[ \left( \sigma +\frac{5\sqrt{2}}{4}\right) -\varphi \right] } := F_5(\varphi ). \end{aligned}$$

(5.28)

The discussion in the previous section shows that there is no smooth traveling waves in this case and since $f(\varphi )$ has no zeros for $\varphi \in \mathbb {R}$, there can only exist cuspons or anticuspons. It is then inferred from (5.28) that $\varphi$ can not oscillate around zero near infinity.

(5.1) $\varphi (x)>0$ near $-\infty$. Then there is some $x_0$ sufficiently large negative so that $\varphi (x_0) = \varepsilon > 0$, with $\varepsilon$ sufficiently small, and $\varphi _x(x_0)>0$. $\sqrt{F_5(\varphi )}$ is locally Lipschitz in $\varphi$ for $0<\varphi <\sigma +\frac{5\sqrt{2}}{4}$, then $\sigma +\frac{5\sqrt{2}}{4}$ becomes a pole of $F_5(\varphi )$. Thus we obtain a traveling wave solution with a cusp at $\varphi = \sigma + \frac{5\sqrt{2}}{4}$ and decay exponentially.

(5.2) $\varphi (x)<0$ near $-\infty$. A directly computation shows that $F'_5(\varphi )<0$ for $\varphi <0$. It is then adduced from the argument applied in Case (2) that there is no traveling wave solution. Hence, the proof of Theorem 5.3 is completed. $\square$