Abstract
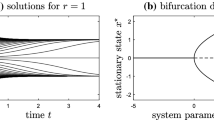
The theory of consensus dynamics is widely employed to study various linear behaviors in networked control systems. Moreover, nonlinear phenomena have been observed in animal groups, power networks and in other networked systems. These observations inspire the development in this paper of three novel approaches to define distributed nonlinear dynamical interactions. The resulting dynamical systems are akin to higher-order nonlinear consensus systems. Over connected undirected graphs, the resulting dynamical systems exhibit various interesting behaviors that we rigorously characterize.
Similar content being viewed by others
References
Arcak, M.: Passivity as a design tool for group coordination. IEEE Trans. Autom. Control 52(8), 1380–1390 (2007)
Ashwin, P., Burylko, O., Maistrenko, Y.: Bifurcation to heteroclinic cycles and sensitivity in three and four coupled phase oscillators. Physica D 237(4), 454–466 (2008)
Bogacz, R., Brown, E., Moehlis, J., Holmes, P., Cohen, J.D.: The physics of optimal decision making: A formal analysis of performance in two-alternative forced choice tasks. Psychol. Rev. 113(4), 700–765 (2006)
Bullo, F., Cortés, J., Martínez, S.: Distributed Control of Robotic Networks. Applied Mathematics Series. Princeton University Press, Princeton (2009). Available at http://www.coordinationbook.info
Couzin, I.D., Krause, J., Franks, N.R., Levin, S.A.: Effective leadership and decision-making in animal groups on the move. Nature 433(7025), 513–516 (2005)
Dionne, B., Golubitsky, M., Stewart, I.: Coupled cells with internal symmetry. Nonlinearity 9, 559–599 (1996)
Dörfler, F., Francis, B.: Geometric analysis of the formation problem for autonomous robots. IEEE Trans. Automat. Contol 55(10), 2379–2384 (2010)
Fax, J.A., Murray, R.M.: Information flow and cooperative control of vehicle formations. IEEE Trans. Autom. Control 49(9), 1465–1476 (2004)
Jadbabaie, A., Lin, J., Morse, A.S.: Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 48(6), 988–1001 (2003)
Khalil, H.K.: Nonlinear Systems, 3rd edn. Prentice Hall, New York (2002)
Kimura, M., Moehlis, J.: Novel vehicular trajectories for collective motion from coupled oscillator steering control. SIAM J. Appl. Dyn. Syst. 7(4), 1191–1212 (2008)
Kwatny, H., Pasrija, A., Bahar, L.: Static bifurcations in electric power networks: Loss of steady-state stability and voltage collapse. IEEE Trans. Circuits Syst. 33(10), 981–991 (1986)
Lin, J., Morse, A.S., Anderson, B.D.O.: The multi-agent rendezvous problem. Part 1: The synchronous case. SIAM J. Control Optim. 46(6), 2096–2119 (2007)
Lorenz, J.: Continuous opinion dynamics under bounded confidence: A survey. Int. J. Mod. Phys. C 18(12), 1819–1838 (2007)
Nabet, B., Leonard, N.E., Couzin, I.D., Levin, S.A.: Dynamics of decision making in animal group motion. J. Nonlinear Sci. 19(4), 399–435 (2009)
Olfati-Saber, R., Fax, J.A., Murray, R.M.: Consensus and cooperation in networked multi-agent systems. Proc. IEEE 95(1), 215–233 (2007)
Olfati-Saber, R., Murray, R.M.: Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 49(9), 1520–1533 (2004)
Olien, L., Bélair, J.: Bifurcations, stability, and monotonicity properties of a delayed neural network model. Physica D 102(3-4), 349–363 (1997)
Papachristodoulou, A., Jadbabaie, A.: Synchronization in oscillator networks with heterogeneous delays, switching topologies and nonlinear dynamics. In: IEEE Conf. on Decision and Control, San Diego, CA, December 2006, pp. 4307–4312 (2006)
Poulakakis, I., Scardovi, L., Leonard, N.E.: Coupled stochastic differential equations and collective decision making in the Two-Alternative Forced-Choice task. In: American Control Conference, pp. 69–74 (2010)
Roxin, A., Ledberg, A.: Neurobiological models of two-choice decision making can be reduced to a one-dimensional nonlinear diffusion equation. PLoS Comput. Biol. 4(3), e1000046 (2008)
Spanos, D.P., Olfati-Saber, R., Murray, R.M.: Approximate distributed Kalman filtering in sensor networks with quantifiable performance. In: Symposium on Information Processing of Sensor Networks, Los Angeles, CA, April 2005, pp. 133–139 (2005)
Srivastava, V., Moehlis, J., Bullo, F.: On bifurcations in nonlinear consensus networks. In: American Control Conference, Baltimore, MD, June 2010, pp. 1647–1652 (2010)
Strogatz, S.H.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Perseus Books Group, New York City (2000)
Tanner, H.G., Jadbabaie, A., Pappas, G.J.: Flocking in fixed and switching networks. IEEE Trans. Autom. Control 52(5), 863–868 (2007)
Wei, J., Ruan, S.: Stability and bifurcation in a neural network model with two delays. Physica D 130(3-4), 255–272 (1999)
Zou, F., Nossek, J.A.: Bifurcation and chaos in cellular neural networks. IEEE Trans. Circuits Syst. I, Fundam. Theory Appl. 40(3), 166–173 (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by R. Sepulchre.
A preliminary version of this work (Srivastava et al. 2010) was presented at the 2010 American Control Conference, Baltimore, MD, USA.
Rights and permissions
About this article
Cite this article
Srivastava, V., Moehlis, J. & Bullo, F. On Bifurcations in Nonlinear Consensus Networks. J Nonlinear Sci 21, 875–895 (2011). https://doi.org/10.1007/s00332-011-9103-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-011-9103-4