Assortment planning for multiple chain stores

Abstract

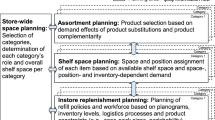
In retail, assortment planning refers to selecting a subset of products to offer that maximizes profit. Assortments can be planned for a single store or a retailer with multiple chain stores where demand varies between stores. In this paper, we assume that a retailer with a multitude of stores wants to specify her offered assortment. To suit all local preferences, regionalization and store-level assortment optimization are widely used in practice and lead to competitive advantages. When selecting regionalized assortments, a trade-off between expensive, customized assortments in every store and inexpensive, identical assortments in all stores that neglect demand variation is preferable. We formulate a stylized model for the regionalized assortment planning problem (APP) with capacity constraints and given demand. In our approach, a common assortment that is supplemented by regionalized products is selected. While products in the common assortment are offered in all stores, products in the local assortments are customized and vary from store to store. The model is both applicable for optimizing a total assortment as well as a particular category of an assortment. Concerning the computational complexity, we show that the APP is strongly NP-hard. We formulate the APP as an integer program and provide algorithms and methods for obtaining approximate solutions and solving large-scale instances. Moreover, we extend our model to include substitution effects. Lastly, we perform computational experiments to analyze the benefits of regionalized assortment planning depending on the variation in customer demands between stores.

Appendix

We present the proof of Theorem 3, which states that the APP can be solved in time ${{\mathscr {O}}}(n^{2^m}+m-1)$.

Proof

Consider an instance of the APP with m stores of size K and n products. In the following, we assume that, in every optimal packing, the common assortment has size strictly less than K. This can be done since, if it has size exactly K, we can simply pack the K items with the largest values $w_j$ into the common assortment to obtain an optimal solution.

We start by sorting, for each bin k individually, the profits $v_{jk}$ for all j in nonincreasing order to obtain m vectors $\nu ^1,\dots ,\nu ^m$ of length n. For each bin, our first packing consists of the first K items with respect to the ordering obtained for this bin. The objective value of this solution is given by $V :=\sum _{k=1}^{m} \sum _{j=1}^{K} (\nu ^k)_j$.

Next, we “guess” the least valuable item $l_k$ in each bin k of a fixed optimal solution that is not part of the common assortment. To do so, we enumerate over all possible combinations of these items in all bins, which are $n^m$ possible combinations. Thus, we assume in the following that we know the least valuable item $l_k$ that is not part of the common assortment in each bin k of a fixed optimal solution. Let $e_k$ be the index of this item with respect to the ordering of the items by nonincreasing profits $v_{jk}$ in bin k. Without loss of generality, we can assume that $e_k \le K$ since, otherwise, $l_k$ could be substituted in the optimal solution by an item with larger local profit in bin k, at least one of which is not part of the common assortment of the optimal solution. Moreover, we can assume that no item with index larger than $e_k$ with respect to the ordering of bin k is part of the individual packing of bin k in the optimal solution since $l_k$ is the least valuable such item in bin k and items with index larger than $e_k$ provide no more individual profit than $l_k$. A consequence is that, in the optimal packing, all items with index smaller or equal to $e_k$ are packed (either into the common assortment or into the individual assortment of bin k). Moreover, if there is an item j such that, for each bin k, its index with respect to the ordering of bin k is smaller than $e_k$, then this item must be part of the common assortment of the optimal solution. We denote the set of these items with index smaller than $e_k$ in the ordering of each bin k by ${\mathscr {J}}$.

Now, we still have to decide which items to pack into the common assortment. Here, we can now restrict our search to the items that have an index larger than $e_k$ in at least one bin k since the other items (which are contained in ${\mathscr {J}}$) are automatically part of the common assortment. Let $S_k$ be the set of the $n-e_k$ items with index larger than $e_k$ in the ordering of bin k. Thus, our remaining task is to decide which items from $S:=\cup _k S_k$ should be packed into the common assortment such that, for each k, exactly $K-e_k$ of these items belong to $S_k$ and the total profit obtained by this process is maximized (no item with index smaller than $e_k$ has to be removed from the packing during this process). We can formulate this problem as the following integer program:

where

$$\begin{aligned} x_j = {\left\{ \begin{array}{ll} 1, \text { if item } j \text { is packed into the common assortment}\\ 0, \text { else} \end{array}\right. } \end{aligned}$$

and $\omega _j$ is the additional profit obtained by packing item j into the common assortment. More formally, for an item j that is not one of the least valuable items $l_1,\dots ,l_m$ in the bins of the optimal solution, we let $T_j$ denote the set of bins where the index of j in the corresponding ordering is smaller than $e_k$. Then, $\omega _j = w_j - \sum _{k \in T_j} v_{jk}$. If j is among the least valuable items $l_1,\dots ,l_m$ in the bins of the optimal solution that we guessed in the first step, we set $\omega _j :=0$ since we know that j is not part of the common assortment in the optimal solution.

We solve the integer program given above by clever enumeration of a suitable subset of the feasible solutions. For each nonempty subset L of the bins, let S(L) denote the set of all items that are contained exactly in those sets $S_k$ corresponding to the bins $k\in L$. Then, by definition, every item in S belongs to exactly one of the sets S(L).

The important observation now is that, if we decide to choose a certain number h of items from some set S(L), the objective value is always maximized by choosing the h items with the largest values $\omega _j$ (breaking ties arbitrarily). Thus, for each nonempty subset L of the bins (of which there are $2^m-1$ many), we only have to choose a number of items from S(L) to pack into the common assortment, which results in $n^{2^m-1}$ potential solutions of the integer program. For each of these potential solutions, we can check in constant time whether it is feasible (i.e., whether it satisfies the m constraints of the integer program) and then select the best solution among the feasible ones in order to obtain an optimal solution.

The running time of the algorithm is dominated by two steps: The “guessing” of the least valuable items takes time ${{\mathscr {O}}}(n^m)$ and solving the integer program by the method described above takes time ${{\mathscr {O}}}(n^{2^m-1})$, which yields the claimed running time. $\square$

Remark 1

Unless $\textsf {P} = \textsf {NP}$, there does not exist an algorithm that solves the integer program in the proof of Theorem 3 in polynomial time in n and m. This can be shown by using a reduction from the independent set problem: Given a graph $G=(V,E)$, we construct a set $S_e = \{x_u,x_v,q\}$ for each edge $e=(u,v)$ in G, where q is a unique dummy item for each set. Further, we set $\omega _u = \omega _v = 1$, $\omega _q = 0$, and $K-e_k = 1$. Then, it is easy to see that an independent set of size p corresponds to a solution of value p of the integer program and vice versa.