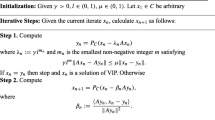Weak Sharpness and Finite Convergence for Solutions of Nonsmooth Variational Inequalities in Hilbert Spaces | Applied Mathematics & Optimization Skip to main content
Springer Nature Link
Log in

Weak Sharpness and Finite Convergence for Solutions of Nonsmooth Variational Inequalities in Hilbert Spaces

  • Published:
Applied Mathematics & Optimization Aims and scope Submit manuscript

Abstract

This paper deals with the study of weak sharp solutions for nonsmooth variational inequalities and finite convergence property of the proximal point method. We present several characterizations for weak sharpness of the solutions set of nonsmooth variational inequalities without using the gap functions. We show that under weak sharpness of the solutions set, the sequence generated by proximal point methods terminates after a finite number of iterations. We also give an upper bound for the number of iterations for which the sequence generated by the exact proximal point methods terminates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alshahrani, M., Al-Homidan, S., Ansari, Q.H.: Minimum and maximum principle sufficiency properties for nonsmooth variational inequalities. Optim. Lett. 10, 805–819 (2016)

    Article  MathSciNet  Google Scholar 

  2. Al-Homidan, S., Ansari, Q.H., Burachik, R.: Weak sharp solutions for generalized variational inequalities. Positivity 21, 1067–1088 (2017)

    Article  MathSciNet  Google Scholar 

  3. Al-Homidan, S., Ansari, Q.H., Nguyen, L.V.: Weak sharp solutions for nonsmooth variational inequalities. J. Optim. Theory Appl. 175, 683–701 (2017)

    Article  MathSciNet  Google Scholar 

  4. Al-Homidan, S., Ansari, Q.H., Nguyen, L.V.: Finite convergence analysis and weak sharp solutions for variational inequalities. Optim. Lett. 11, 1647–1662 (2017)

    Article  MathSciNet  Google Scholar 

  5. Ansari, Q.H., Lalitha, C.S., Mehta, M.: Generalized Convexity, Nonsmooth Variational Inequalities and Nonsmooth Optimization, CRC Press. Taylor & Francis Group, Boca Raton (2014)

    MATH  Google Scholar 

  6. Bertsekas, D.P.: Necessary and sufficient conditions for a penality method to be exact. Math. Program. 9, 8–99 (1975)

    Article  MathSciNet  Google Scholar 

  7. Burke, J.V., Ferris, M.C.: Weak sharp minima in mathematical programming. SIAM J. Control Optim. 31, 1340–1359 (1993)

    Article  MathSciNet  Google Scholar 

  8. Combettes, P.L., Hirstoaga, A.: Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 6, 117–136 (2005)

    MathSciNet  MATH  Google Scholar 

  9. Fan, K.: A generalization of Tychonoff’s fixed point theorem. Math. Ann. 142, 305–310 (1961)

    Article  MathSciNet  Google Scholar 

  10. M.C. Ferris, Weak Sharp Minima and Penalty Functions in Mathematical Programming, Ph.D. Thesis, University of Cambridge (1988)

  11. Ferris, M.C.: Finite termination of the proximal point algorithm. Math. Program. 50, 359–366 (1991)

    Article  MathSciNet  Google Scholar 

  12. Huang, H., He, M.: Weak sharp solutions of mixed variational inequalities in Banach spaces. Optim. Lett. 12, 287–299 (2018)

    Article  MathSciNet  Google Scholar 

  13. Hua, Y.H., Song, W.: Weak sharp solutions for variational inequalities in Banach spaces. J. Math. Anal. Appl. 374, 118–132 (2011)

    Article  MathSciNet  Google Scholar 

  14. Jayswal, A., Singh, S.: Characterization of weakly sharp solutions of a variational-type inequality with convex functional. Ann. Oper. Res. (2017). https://doi.org/10.1007/s10479-017-2700-3

    Article  MATH  Google Scholar 

  15. László, S.: Multivalued variational inequalities and coincidence point results. J. Math. Anal. Appl. 404, 105–114 (2013)

    Article  MathSciNet  Google Scholar 

  16. Liu, Y., Wu, Z.: Characterization of weakly sharp solutions of a variational inequality by its primal gap function. Optim. Lett. 10, 563–576 (2016)

    Article  MathSciNet  Google Scholar 

  17. Marcotte, P., Zhu, D.L.: Weak sharp solutions of variational inequalities. SIAM J. Optim. 9, 179–189 (1998)

    Article  MathSciNet  Google Scholar 

  18. Matsushita, S., Xu, L.: Finite convergence of the proximal point algorithm for variational inequality problems. Set-Valued Var. Anal. 21, 297–309 (2013)

    Article  MathSciNet  Google Scholar 

  19. Matsushita, S., Xu, L.: On finite convergence of iterative methods for variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 161, 701–715 (2014)

    Article  MathSciNet  Google Scholar 

  20. Patriksson, M.: A Unified Framework of Descent Algorithms for Nonlinear Programs and Variational Inequalities. Department of Mathematics, Linkoping Institute of Technology, Linkoping (1993). Ph.D. Thesis

    Google Scholar 

  21. Xiong, J., Li, J.: Weak sharpness for set-valued variational inequalities and applications to finite termination of iterative algorithms. Optimization 65, 1585–1597 (2016)

    Article  MathSciNet  Google Scholar 

  22. Xiu, N., Zhang, J.: On finite convergence of proximal point algorithms for variational inequalities. J. Math. Anal. Appl. 312, 148–158 (2005)

    Article  MathSciNet  Google Scholar 

  23. Wu, Z.L., Wu, S.Y.: Weak sharp solutions of variational inequalities in Hilbert spaces. SIAM J. Optim. 14, 1011–1027 (2004)

    Article  MathSciNet  Google Scholar 

  24. Wu, Z.: Characterizations of weakly sharp solutions for a variational inequality with a pseudomonotone mapping. Eur. J. Oper. Res. 265, 448–453 (2018)

    Article  MathSciNet  Google Scholar 

  25. Zhou, J., Chen, G.: Diagonal convexity conditions for problems in convex analysis and quasivariational inequalities. J. Math. Anal. Appl. 132, 213–225 (1988)

    Article  MathSciNet  Google Scholar 

  26. Zhou, J., Wang, C.: A note on finite termination of iterative algorithms in mathematical programming. Oper. Res. Lett. 36, 715–717 (2008)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This article was supported by the National Natural Science Foundation of China under Grant No.11401152. The first author was also supported by the Research Fund for International Young Scientists under Grant No. 1181101157 and the China Postdoctoral Science Foundation under Grant No. 2017M620042. The main part of this paper was done when the first author was a postdoc at UESTC, China.

Author information

Authors and Affiliations

  1. Department of Natural Sciences, Hong Duc University, Thanh Hoa, Vietnam

    Luong V. Nguyen

  2. Department of Mathematics, Aligarh Muslim University, Aligarh, India

    Qamrul Hasan Ansari

  3. Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia

    Qamrul Hasan Ansari

  4. Department of Mathematics, Hangzhou Normal University, Hangzhou, China

    Xiaolong Qin

Authors
  1. Luong V. Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qamrul Hasan Ansari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaolong Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaolong Qin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, L.V., Ansari, Q.H. & Qin, X. Weak Sharpness and Finite Convergence for Solutions of Nonsmooth Variational Inequalities in Hilbert Spaces. Appl Math Optim 84, 807–828 (2021). https://doi.org/10.1007/s00245-020-09662-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00245-020-09662-7

Keywords

Mathematics Subject Classification

Search

Navigation