Abstract
A unified framework for fourth-order semilinear problems with trilinear nonlinearity and general sources allows for quasi-best approximation with lowest-order finite element methods. This paper establishes the stability and a priori error control in the piecewise energy and weaker Sobolev norms under minimal hypotheses. Applications include the stream function vorticity formulation of the incompressible 2D Navier-Stokes equations and the von Kármán equations with Morley, discontinuous Galerkin, \(C^{0}\) interior penalty, and weakly over-penalized symmetric interior penalty schemes. The proposed new discretizations consider quasi-optimal smoothers for the source term and smoother-type modifications inside the nonlinear terms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The abstract framework for fourth-order semilinear elliptic problems with trilinear nonlinearity in this paper allows a source term \(F \in H^{-2}(\Omega )\) in a bounded polygonal Lipschitz domain \(\Omega \). It simultaneously applies to the Morley finite element method (FEM) [8, 15], the discontinuous Galerkin (dG) FEM [18], the \(C^0\) interior penalty (\(C^0\)IP) method [3], and the weakly over-penalized symmetric interior penalty (WOPSIP) scheme [1] for the approximation of a regular solution to a fourth-order semilinear problem with the biharmonic operator as the leading term. In comparison to [8], this article includes dG/\(C^0\)IP/WOPSIP schemes and more general source terms that allow single forces. It thereby continues [11] for the linear biharmonic equation to semilinear problems and, for the first time, establishes quasi-best approximation results for a discretisation by the Morley/dG/\(C^0\)IP schemes with smoother-type modifications in the nonlinearities.
A general source term \(F\in H^{-2}(\Omega )\) cannot be immediately evaluated at a possibly discontinuous test function \(v_h \in V_h \not \subset H^2_0(\Omega )\) for the nonconforming FEMs of this paper. The post-processing procedure in [3] enables a new \(C^0\)IP method for right-hand sides in \(H^{-2}(\Omega )\). The articles [25,26,27] employ a map Q, referred to as a smoother, that transforms a nonsmooth function \(y_h\) to a smooth version \(Qy_h\). The discrete schemes are modified by replacing F with \(F\circ Q\) and the quasi-best approximation follows for Morley and \(C^0\)IP schemes for linear problems in the energy norm. The quasi-optimal smoother \(Q=JI_{\textrm{M}}\) in [11] for dG schemes is based on a (generalised) Morley interpolation operator \(I_\text {M}\) and a companion operator J from [12, 19].
In addition to the smoother Q in the right-hand side, this article introduces operators \(R, S \in \{\textrm{id}, I_\text {M}, JI_\text {M}\}\) in the trilinear form \(\Gamma _{\textrm{pw}}(Ru_h, Ru_h, Sv_h)\) that lead to nine new discretizations for each of the four discretization schemes (Morley/dG/\(C^0\)IP/WOPSIP) in two applications. Here \(R,S =\textrm{id}\) means no smoother, \(I_\text {M}\) is averaging in the Morley finite element space, while \(J I_\text {M}\) is the quasi-optimal smoother. The simultaneous analysis applies to the stream function vorticity formulation of the 2D Navier-Stokes equations [6, 13, 14] and von Kármán equations [16, 23] defined on a bounded polygonal Lipschitz domain \(\Omega \) in the plane. For \(S=JI_\text {M}\) and all \(R \in \{\textrm{id}, I_\text {M}, JI_\text {M}\}\), the Morley/dG/\(C^0\)IP schemes allow for the quasi-best approximation
Duality arguments lead to optimal convergence rates in weaker Sobolev norm estimates for the discrete schemes with specific choices of R in the trilinear form summarised in Table 1. The comparison results suggest that, amongst the lowest-order methods for fourth-order semilinear problems with trilinear nonlinearity, the attractive Morley FEM is the simplest discretization scheme with optimal error estimates in (piecewise) energy and weaker Sobolev norms.
For \(F \in H^{{-r}}(\Omega )\) with \(2-\sigma \le r \le 2\) (with the index of elliptic regularity \(\sigma _{\textrm{reg}}>0\) and \(\sigma {{:}{=}}\min \{\sigma _{\textrm{reg}},1\}>0\) ) and for the biharmonic, the 2D Navier-Stokes, and the von Kármán equations with homogeneous Dirichlet boundary conditions, it is known that the exact solution belongs to \(H^2_0(\Omega )\cap H^{4-r} (\Omega )\).
Organisation. The remaining parts are organised as follows. Section 2 discusses an abstract discrete inf-sup condition for linearised problems. Section 3 introduces the main results (A)-(C) of this article. Section 4 discusses the quadratic convergence of Newton’s scheme and the unique existence of a local discrete solution \(u_h\) that approximates a regular root \(u \in H^2_0(\Omega )\) for data \(F \in H^{-2}(\Omega )\). Section 5 presents an abstract a priori error control in the piecewise energy norm with a quasi-best approximation for \(S = JI_{\textrm{M}}\) in (1.1). Section 6 discusses the goal-oriented error control and derives an a priori error estimate in weaker Sobolev norms. There are at least two reasons for this abstract framework enfolded in Sects. 2–6. First it minimizes the repetition of mathematical arguments in two important applications and four popular discrete schemes. Second, it provides a platform for further generalizations to more general smooth semilinear problems as it derives all the necessities for the leading terms in the Taylor expansion of a smooth semilinearity. Section 7 presents preliminiaries, triangulations, discrete spaces, the conforming companion, discrete norms and some auxiliary results on \(I_\text {M}\) and J. Sections 8 and 9 apply the abstract results to the stream function vorticity formulation of the 2D Navier-Stokes and the von Kármán equations for the Morley/dG/\(C^0\)IP/WOPSIP approximations. They contain comparison results and convergence rates displayed in Table 1.
2 Stability
This section establishes an abstract discrete inf-sup condition under the assumptions (2.1)–(2.3), (2.5), (2.8) and (H1)-(H3) stated below. This is a key step and has consequences for second-order elliptic problems (as in [8, Section 2]) and in this paper for the well-posedness of the discretization. In comparison to [8] that merely addresses nonconforming FEM, the proof of the stability in this section applies to all the discrete schemes. Let \({\widehat{X}}\) (resp. \({\widehat{Y}}\)) be a real Banach space with norm \(\Vert \bullet \Vert _{{\widehat{X}}}\) (resp. \(\Vert \bullet \Vert _{{\widehat{Y}}}\)) and suppose X and \(X_h\) (resp. Y and \(Y_h\)) are two complete linear subspaces of \({\widehat{X}}\) (resp. \({\widehat{Y}}\)) with inherited norms \(\Vert \bullet \Vert _{X}{{:}{=}}\big (\Vert \bullet \Vert _{{\widehat{X}}}\big )|_{X}\) and \(\Vert \bullet \Vert _{X_h}{{:}{=}}\big (\Vert \bullet \Vert _{{\widehat{X}}}\big )|_{X_h}\) (resp. \(\Vert \bullet \Vert _{Y}{{:}{=}}\big (\Vert \bullet \Vert _{{\widehat{Y}}}\big )|_{Y}\) and \(\Vert \bullet \Vert _{Y_h}{{:}{=}}\big (\Vert \bullet \Vert _{{\widehat{Y}}}\big )|_{Y_h}\)); \(X + X_h \subseteq {\widehat{X}}\) and \(Y + Y_h \subseteq {\widehat{Y}}\).
Table 2 summarizes the bounded bilinear forms and associated operators with norms. Let the linear operators \({A}\in L({X}; {Y}^*)\) and \(A+B\in L(X;Y^*)\) be associated to the bilinear forms a and \(a+b\) and suppose A and \(A+B\) are invertible so that the inf-sup conditions
hold. Assume that the linear operator \(A_{h} : X_{h} \rightarrow Y_{h}^*\) is invertible and
holds for some universal constant \(\alpha _0\). Let the linear operators \(P \in L(X_h;X)\), \(Q \in L(Y_h;Y)\), \(R\in L(X_h;{\widehat{X}})\), \(S \in L(Y_h; {\widehat{Y}})\) and the constants \(\Lambda _{\textrm{P}},\Lambda _{\textrm{Q}}, \Lambda _{\textrm{R}}, \Lambda _{\textrm{S}}\ge 0\) satisfy
Suppose the operator \(I_{\textrm{X}_h} \in L(X ;X_h)\), the constants \(\Lambda _1, \delta _2\), \(\delta _3 \ge 0,\) the above bilinear forms \(a,\,a_h, {{\widehat{b}}}\), and the linear operator A from Table 2 satisfy, for all \(x_h \in X_h,\,y_h \in Y_h,\,x \in X,\) and \(y \in Y\), that
- (H1):
-
\( a_h(x_h,y_h)-a(Px_h,Qy_h)\le \Lambda _{1}\Vert x_h - Px_h\Vert _{{\widehat{X}}} \Vert y_h \Vert _{Y_h},\)
- (H2):
-
\(\displaystyle \delta _2 {{:}{=}} \sup _{\begin{array}{c} x_h\in X_h\\ \Vert x_h\Vert _{X_h}=1 \end{array}} \Vert (1 - I_{\textrm{X}_h}) A^{-1}({{\widehat{b}}}(Rx_h,\bullet )|_{Y})\Vert _{{\widehat{X}}},\)
- (H3):
-
\(\displaystyle \delta _3{{:}{=}}\sup _{\begin{array}{c} x_h\in X_h\\ \Vert x_h\Vert _{X_h}=1 \end{array}}\Vert {{\widehat{b}}}(Rx_h,(Q-S)\bullet \big )\Vert _{ Y_h^*}\).
In applications, we establish that \(\delta _2\) and \(\delta _3\) are sufficiently small. Given \(\alpha \), \(\beta \), \(\alpha _h\), \(\Lambda _{\textrm{P}}\), \(\Lambda _{1}\), \(\Lambda _{\textrm{R}}\), \(\delta _{2}\), \(\delta _{3}\) from above and the norms \(\Vert A\Vert \) and \(\Vert {{\widehat{b}}}\Vert \) from Table 2, define
with the adjoint \(Q^*\) of Q. In all applications of this article, \(1/\alpha \), \(1/\beta \), \(1/\alpha _h\), \(\Lambda _{\textrm{P}}\), \(\Lambda _{\textrm{Q}}\), \(\Lambda _{\textrm{R}}\), \(\Lambda _{\textrm{S}}\), \(\Lambda _{1}\), and \(\Vert Q^*A\Vert \) are bounded from above by generic constants, while \(\delta _2\) and \(\delta _3\) are controlled in terms of the maximal mesh-size \(h_{\textrm{max}}\) of an underlying triangulation and tend to zero as \(h_{\textrm{max}} \rightarrow 0\). Hence, \(\beta _0 > 0\) is positive for sufficiently fine triangulations and even bounded away from zero, \(\beta _0 \gtrsim 1\). (Here \(\beta _0 \gtrsim 1\) means \(\beta _0 \ge C\) for some positive generic constant C.) This enables the following discrete inf-sup condition.
Theorem 2.1
(discrete inf-sup condition) Under the aforementioned notation, (2.1)–(2.3), (2.5), (2.8) and (H1)–(H3) imply the stability condition
Before the proof of Theorem 2.1 completes this section, some remarks on the particular choices of R and S are in order to motivate the general description.
Example 2.2
(quasi-optimal smoother \(JI_\text {M}\)) This paper follows [11] in the definition of the quasi-optimal smoother \(P=Q=JI_\text {M}\) in the applications with \(X=Y=V=:H^2_0(\Omega )\) for the biharmonic operator A and the linearisation B of the trilinear form. Then (2.3)–(2.4) follow in Sect. 7.3 below; cf. Definition 7.2 (resp. Lemma 7.4) for the definition of the Morley interpolation \(I_{\textrm{M}}\) (resp. the companion operator J).
Example 2.3
(no smoother in nonlinearity) The natural choice in the setting of Example 2.2 reads \(R=\textrm{id}=S\) [8]. Then \(\Lambda _{\textrm{R}}=0 =\Lambda _{\textrm{S}} \) in (2.5)–(2.6) and a priori error estimates will be available for the respective discrete energy norms. However, only a few optimal convergence results shall follow for the error in the piecewise weaker Sobolev norms, e.g., for the Morley scheme for the Navier-Stokes (Theorem 8.5.c) and for the von Kármán equations (Theorem 9.3.b).
Example 2.4
(smoother in nonlinearity) The choices \(R=P\) and \(S=Q\) lead to \(\Lambda _{\textrm{R}} = \Lambda _\textrm{P}\) and \(\Lambda _{\textrm{S}}= \Lambda _{\textrm{Q}}\) in (2.5)–(2.6), while \(\delta _3=0\) in (H3). This allows for optimal a priori error estimates in the piecewise energy and in weaker Sobolev norms and this is more than an academic exercise for a richer picture on the respective convergence properties; cf. [10] for exact convergence rates for the Morley FEM. This is important for the analysis of quasi-orthogonality in the proof of optimal convergence rates of adaptive mesh-refining algorithms in [9].
Example 2.5
(simpler smoother in nonlinearity) The realisation of \({R=S=P=JI_\text {M}}\) in the setting of Example 2.2 may lead to cumbersome implementations in the nonlinear terms and so the much cheaper choice \(R=S=I_\text {M}\) shall also be discussed in the applications below.
Remark 2.6
(on (H1)) The paper [11] adopts [25]-[27] and extends those results to the dG scheme as a preliminary work on linear problems for this paper. The resulting abstract condition \(\mathbf{(H1)}\) therein is a key property to analyze the linear terms simultaneously.
Remark 2.7
(comparison with [8]) The set of hypotheses for the discrete inf-sup condition in this article differs from those in [8]. This paper allows smoothers in the nonlinear terms and also applies to dG/\(C^0\)IP/WOPSIP schemes.
Remark 2.8
(consequences of (2.3)–(2.6)) The estimates in (2.3)–(2.6) give rise to a typical estimate utilised throughout the analysis in this paper. For instance, (2.3) (resp. (2.5)) and a triangle inequality show, for all \(x\in X\) and \(x_h \in X_h\), that
The analog (2.4) (resp. (2.6)) leads, for all \(y \in Y\) and \(y_h \in Y_h\), to
Proof of Theorem 2.1
The proof of Theorem 2.1 departs as in [8, Theorem 2.1] for nonconforming schemes for any given \(x_h\in X_h\) with \(\Vert x_h\Vert _{X_h}=1\). Define
The definitions of \(\xi \in X\) and \(\xi _h \in X_h\) lead in (H2) to
The second inf-sup condition in (2.1) and \(A\eta =Bx \in Y^*\) result in
with the operator norm of A in the last step. This and triangle inequalities imply
The above definitions of \(\xi \) and \(\eta \) guarantee \(a(\xi -\eta ,\bullet ) = {{\widehat{b}}}(Rx_h - x,\bullet )\vert _{Y} \in Y^{*}\). This, (2.1), and the norm \(\Vert {{\widehat{b}}}\Vert \) of the bilinear form \({{\widehat{b}}}\) show
with (2.10) in the last step. Note that the definition \(x =P x_h\) and (2.3) imply
The combination of (2.13)–(2.14) results in
A triangle inequality, (2.14)–(2.15), and the definition of \({{\widehat{\beta }}}\) in (2.7) lead to
This in the first inequality below and a triangle inequality plus (2.12) show
The condition (2.2) implies for \(x_h + \xi _h \in X_h\) and for any \(\epsilon >0\), the existence of some \(\phi _h \in Y_h\) such that \( \Vert \phi _h\Vert _{Y_h} \le 1+ {\epsilon }\) and \(\alpha _h \Vert x_h + \xi _h\Vert _{X_h} = a_h(x_h + \xi _h,\phi _h).\) Elementary algebra shows
and motivates the control of the terms below.
Hypothesis (H1) and (2.3) imply
with (2.12) and \(\Vert \phi _h\Vert _{Y_h} \le 1 + \epsilon \) in the last step above. The boundedness of \(Q^{*}A \in L(X; Y_h^*)\), \(\Vert \phi _h\Vert _{Y_h} \le 1 + \epsilon \), (2.10), and (2.12) for \(\Vert \xi - P \xi _h \Vert _{X} \le (1 + \Lambda _{\textrm{P}}) \Vert \xi - \xi _h \Vert _{{\widehat{X}}} \le (1 + \Lambda _{\textrm{P}}) \delta _2\) reveal
The definition of \(\xi \) shows that \(a(\xi ,Q\phi _h) ={{\widehat{b}}}(Rx_h,Q\phi _h)\). This, \(\Vert \phi _h\Vert _{Y_h} \le 1 + \epsilon \), and (H3) imply
The combination of (2.17)- (2.20) reads
This, (2.16), and \(\Vert \phi _h\Vert _{Y_h} \le 1+\epsilon \) imply \(\alpha _h {{\widehat{\beta }}} \le {} (\Vert a_h(x_h,\bullet ) + {\widehat{b}}(R x_h,S \bullet ) \Vert _{Y_h^*} +(\Vert Q^{*}A\Vert (1+\Lambda _{\textrm{P}})+\Lambda _{1}\Lambda _\textrm{P})\delta _2+\delta _3\big )(1 + \epsilon )+\alpha _h \delta _2. \) This and (2.8) demonstrate
At this point, we may choose \(\epsilon \searrow 0\) and obtain
Since \(x_h \in X_h\) is arbitrary with \(\Vert x_h \Vert _{X_h} = 1\), this proves the discrete inf-sup condition (2.9). (In this section \(Y_h\) is a closed subspace of the Banach space \({\widehat{Y}}\) and not necessarily reflexive. In the sections below, \(Y_h\) is finite-dimensional and the above arguments apply immediately to \(\epsilon =0\).) \(\square \)
3 Main results
This section introduces the continuous and discrete nonlinear problems, associated notations, and states the main results of this article in (A)-(C) below. The paper has two parts written in abstract results of Sects. 2, 4–6 and their applications in Sects. 8-9. In the first part, the hypotheses (H1)-(H3) in the setting of Sect. 2 and the hypothesis (H4) stated below guarantee the existence and uniqueness of an approximate solution for the discrete problem, feasibility of an iterated Newton scheme, and an a priori energy norm estimate in (A)-(B). An additional hypothesis (\(\widehat{{\textbf {H1}}}\)) enables a priori error estimates in weaker Sobolev norms stated in (C). The second part in Sects. 8-9 verifies the abstract results for the 2D Navier-Stokes equations in the stream function vorticity formulation and for the von Kármán equations.
Adopt the notation on the Banach spaces X and Y (with \(X_h, {\widehat{X}}\) and \(Y_h, {\widehat{Y}}\)) of the previous section and suppose that the quadratic function \(N:X \rightarrow Y^*\) is
with a bounded linear operator \(A \in L(X;Y^*)\), a bounded trilinear form \(\Gamma : X\times X\times Y\rightarrow {\mathbb {R}}\), and a linear form \(F\in Y^*\). Suppose there exists a bounded trilinear form \( {{\widehat{\Gamma }}}:{\widehat{X}}\times {\widehat{X}}\times {\widehat{Y}}\rightarrow {\mathbb {R}}\) with \(\Gamma ={{\widehat{\Gamma }}}|_{X\times X\times Y}\), \(\Gamma _h={{\widehat{\Gamma }}}|_{X_h\times X_h\times Y_h}\), and let
The linearisation of \({{\widehat{\Gamma }}}\) at \(u \in X\) defines the bilinear form \({{\widehat{b}}}:{\widehat{X}}\times {\widehat{Y}}\rightarrow {{\mathbb {R}}}\),
The boundedness of \( {{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\) applies to (3.2) and provides \(\Vert {{\widehat{b}}}\Vert \le 2\Vert {{\widehat{\Gamma }}}\Vert \Vert u\Vert _X \).
Definition 3.1
(regular root) A function \(u \in X\) is a regular root to (3.1), if u solves
and the Frechét derivative \(DN(u)=:(a+b)(\bullet ,\bullet )\) defines an isomorphism \(A+B\) and in particular satisfies the inf-sup condition (2.1) for \(b{{:}{=}}{\widehat{b}}|_{X \times Y}\) and \({\widehat{b}}\) from (3.2). \(\square \)
Abbreviate \((a+b)(x,y){{:}{=}}a(x,y)+b(x,y)\) etc. Several discrete problems in this article are defined for different choices of \(R\) and \(S\) with (2.5)–(2.6) to approximate the regular root u to N. In the applications of Sects. 8-9, \( R, S\in \{\text {id},I_{\text {M}}, JI_{\text {M}}\}\) lead to eight new discrete nonlinearities. Let \(X_h\) and \(Y_h\) be finite-dimensional spaces and let
The discrete problem seeks a root \(u_h \in X_h\) to \(N_h\); in other words it seeks \(u_h \in X_h\) that satisfies
The local discrete solution \(u_h \in X_h\) depends on R and S (suppressed in the notation).
Suppose
- (H4):
-
\(\exists x_h \in X_h\) such that \(\delta _4 {{:}{=}} \Vert u- x_h\Vert _{{\widehat{X}}}<\beta _0/2 (1 + \Lambda _{\textrm{R}}) \Vert {{\widehat{\Gamma }}}\Vert \Vert R\Vert \Vert S\Vert \),
so that, in particular,
The non-negative parameters \(\Lambda _1, \delta _2,\delta _3,\,\delta _4\), \(\beta \), and \(\Vert {{\widehat{b}}}\Vert \) depend on the regular root u to N (suppressed in the notation).
The hypotheses (H1)-(H4) with sufficiently small \(\delta _2,\) \(\delta _3\), \(\delta _4\) imply the results stated in (A)-(B) below for parameters \(\epsilon _1, \epsilon _2, \delta , \rho ,\) \(C_{\textrm{qo}}>0\) and \(0< \kappa <1\), such that (A)-(B) hold for any underlying triangulation \({\mathcal {T}}\) with maximum mesh-size \(h_{\textrm{max}} \le \delta \) in the applications of this article.
- (A):
-
local existence of a discrete solution. There exists a unique discrete solution \(u_h\in X_h \) to \(N_h(u_h)=0\) in (3.5) with \(\Vert u-u_h\Vert _{{\widehat{X}}} \le \epsilon _1\). For any initial iterate \(v_h \in X_h\) with \(\Vert u_h-v_h\Vert _{{X_h}} \le \rho \), the Newton scheme converges quadratically to \(u_h\).
- (B):
-
a priori error control in energy norm. The continuous (resp. discrete) solution \(u \in X\) (resp. \(u_h \in X_h\)) with \(\Vert u-u_h\Vert _{{\widehat{X}}} \le \epsilon _2{{:}{=}}\min \left\{ \epsilon _1, \frac{ \kappa \beta _1}{ (1+ \Lambda _{\textrm{R}})^2\Vert S\Vert \Vert {{\widehat{\Gamma }}}\Vert } \right\} \) satisfies
$$\begin{aligned} \displaystyle \Vert u - u_h \Vert _{{\widehat{X}}} \le C_{\textrm{qo}} \min _{x_h \in X_h} \Vert u - x_{h}\Vert _{{\widehat{X}}} + {\beta ^{-1}_1(1-\kappa )^{-1}}{\Vert {{\widehat{\Gamma }}}(u,u,(S-Q)\bullet ) \Vert _{Y_h^*} } \end{aligned}$$with a lower bound \(\beta _1\) of \(\beta _h\) defined in (3.6). The quasi-best approximation result (1.1) holds for \(S=Q\).
- (C):
-
a priori error control in weaker Sobolev norms. In addition to (H1)–(H4), suppose the existence of \(\Lambda _5>0\) such that, for all \(x_h \in X_h\), \(y_h \in Y_h\), \(x \in X\), and \(y \in Y\),
- (\(\widehat{{\textbf {H1}}}\)):
-
\(a_h(x_h,y_h)-a(Px_h,Qy_h)\le \Lambda _{5}\Vert x - x_h\Vert _{{\widehat{X}}} \Vert y - y_h \Vert _{{\widehat{Y}}}\).
For any \(G \in X^{*}\), if \(z \in Y\) solves the dual linearised problem \(a(\bullet ,z) + b(\bullet ,z) = G(\bullet )\) in \(X^*\), then any \(z_h \in Y_h\) satisfies
$$\begin{aligned}&\Vert u - u_h \Vert _{X_{\textrm{s}}} \le \omega _1(\Vert u\Vert _X , \Vert u_h\Vert _{X_h})\Vert z - z_h \Vert _{{\widehat{Y}}} \Vert u - u_h \Vert _{{\widehat{X}}} \\&\quad + \omega _2(\Vert z_h\Vert _{Y_h}) \Vert u - u_{h} \Vert ^2_{{\widehat{X}}} \\&\quad + \Vert u_h - Pu_h\Vert _{X_{\textrm{s}}} + {{\widehat{\Gamma }}}(u,u,(S-Q)z_h) \\&\quad + {{\widehat{\Gamma }}}(Ru_h,Ru_h,Q z_h) -{\Gamma }(Pu_h,Pu_h,Q z_h) \end{aligned}$$with appropriate weights defined in (6.2) below. Here \(X_{\textrm{s}}\) is a Hilbert space with \(X+X_h \subset X_{\textrm{s}}\).
The abstract results (A)-(C) are established in Theorems 4.1, 5.1, and 6.2. A summary of their consequences in the applications in Sects. 8-9 for a triangulation with sufficiently small maximal mesh-size \(h_{\textrm{max}}\) is displayed in Table 1.
4 Existence and uniqueness of discrete solution
This section applies the Newton-Kantorovich convergence theorem to establish (A). Let \(u\in X\) be a regular root to N. Let (2.3), (2.5), and (H1)-(H4) hold with parameters \(\Lambda _\textrm{P},\,\Lambda _{\textrm{R}},\,\Lambda _{1},\,\delta _2,\) \(\,\delta _3,\) \(\,\delta _4 \ge 0\). Define \(L {{:}{=}} 2 \Vert {{\widehat{\Gamma }}}\Vert \Vert R\Vert ^2 \Vert S\Vert \), \(m {{:}{=}}L/ \beta _1\), and
In this section (and in Sect. 5 below), \(Q \in L(Y_h;Y)\) (resp. \(S \in L(Y_h; {\widehat{Y}})\)) is bounded, but (2.4) (resp. (2.6)) is not employed.
Theorem 4.1
(existence and uniqueness of a discrete solution) (i) If \(\epsilon _0 m \le 1/2\), then there exists a root \(u_h \in X_h\) of \(N_h\) with \(\Vert u-u_h \Vert _{{\widehat{X}}} \le \epsilon _1 {{:}{=}} \delta _4 + (1-\sqrt{1-2 \epsilon _0 m })/m. \)
(ii) If \(\epsilon _0 m < 1/2\), then given any \(v_h\in X_h\) with \(\Vert u_h - v_h\Vert _{{X_h}}\le \rho {{:}{=}} (1+\sqrt{1-2 \epsilon _0 m})/ m>0\), the Newton scheme with initial iterate \(v_h\) converges quadratically to the root \(u_h\) to \(N_h\) in (i).
(iii) If \( \epsilon _1 m \le 1/2\), then there exists at most one root \(u_h\) to \(N_h\) with \(\Vert u-u_h \Vert _{{\widehat{X}}}\le \epsilon _1\).
The proof of Theorem 4.1 applies the well-known Newton-Kantorovich convergence theorem found, e.g., in [21, Subsection 5.5] for \( X= Y={\mathbb {R}}^n\) and in [28, Subsection 5.2] for Banach spaces. The notation is adapted to the present situation.
Theorem 4.2
(Kantorovich (1948)) Assume the Frechét derivative \(DN_h(x_h)\) of \(N_h\) at some \(x_h\in X_h\) satisfies
Suppose that \(D N_h\) is Lipschitz continuous with Lipschitz constant L and that \( 2 \epsilon _0 L \le \beta _1\). Then there exists a root \(u_h\in \overline{ B(x_1,r_-)} \) of \(N_h\) in the closed ball around the first iterate \(x_1 {{:}{=}} x_h - D N_h(x_h)^{-1}N_h(x_h)\) of radius \(r_-{{:}{=}} (1-\sqrt{1-2 \epsilon _0 m })/m - {\epsilon _0}\) and this is the only root of \(N_h\) in \(\overline{B(x_h,\rho )}\) with \(\rho {{:}{=}} (1+\sqrt{1-2 \epsilon _0 m})/ m\). If \(2 \epsilon _0 L < \beta _1\), then the Newton scheme with initial iterate \(x_h\) leads to a sequence in \(B(x_h,\rho )\) that converges R-quadratically to \(u_h\). \(\square \)
Proof of Theorem 4.1. Step 1 establishes (4.2). The bounded trilinear form \({{\widehat{\Gamma }}}\) leads to the Frechét derivative \(DN_h( x_h)\in L(X_h;Y_h^*)\) of \(N_h\) from (3.4) evaluated at any \(x_h \in X_h\) for all \(\xi _h\in X_h\), \(\eta _h\in Y_h\) with
For any \(x_h^1, x_h^2, \xi _h \in X_h\) and \(\eta _h \in Y_h\), (4.3) implies the global Lipschitz continuity of \(DN_h\) with Lipschitz constant \(L{{:}{=}} 2 \Vert {{\widehat{\Gamma }}}\Vert \Vert R\Vert ^{2} \Vert S\Vert \), and so
Recall \(x_h\) from (H4) with \(\delta _4 = \Vert u- x_h\Vert _{{\widehat{X}}}\). For this \(x_h \in X_h\), (2.10) leads to \(\Vert u-Rx_h\Vert _{{\widehat{X}}} \le (1+\Lambda _{\textrm{R}}) \delta _4\). This and the boundedness of \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\) show
The discrete inf-sup condition in Theorem 2.1, elementary algebra, and the above displayed estimate establish a positive inf-sup constant
for the discrete bilinear form (4.3). The inf-sup constant \(\beta _1 > 0\) in (4.4) is known to be (an upper bound of the) reciprocal of the operator norm of \(DN_h(x_h)\) and that provides the first estimate in (4.2). It also leads to
To establish the second inequality in (4.2), for any \(y_h\in Y_h\) with \(\Vert y_h\Vert _{Y_h}=1\), set \(y{{:}{=}}Q y_h\in Y.\) Since \(N(u;y)=0\), (3.3)-(3.4) reveal
The combination of (H1) and (2.3) results in
with the operator norm \(\Vert Q^{*}A\Vert \) of \(Q^*A\) in \(L(X;Y_h^*)\) in the last step. Utilize (2.10) and (H4) to establish \(\Vert u - Px_{h}\Vert _{X} \le (1 + \Lambda _{\textrm{P}}) \delta _4 \). This and the previous estimates imply
Elementary algebra and the boundedness of \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\), (2.5), and (H3)-(H4) show
A combination of the two above displayed estimates in (4.6) reveals
This implies \(\Vert N_h(x_h)\Vert _{Y_h^*}\le \beta _1{\epsilon _0} \) with \({\epsilon _0}\ge 0\) from (4.1). The latter bound leads in (4.5) to the second condition in (4.2).
Step 2 establishes the assertion (i) and (ii). Since \(\epsilon _0 m \le 1/2\), \( r_-, \rho \ge 0\) is well-defined, \(2 \epsilon _0 L \le \beta _1\), and hence Theorem 4.2 applies.
We digress to discuss the degenerate case \(\epsilon _0 = 0\) where (4.1) implies \(\delta _4 = 0\). An immediate consequence is that (H4) results in \(u = x_h \in X_h\). The proof of Step 1 remains valid and \(N_h(x_h) = 0\) (since \(\epsilon _0 = 0\)) provides that \(x_h = u\) is the discrete solution \(u_h\). Observe that in this particular case, the Newton iterates form the constant sequence \(u= x_h = x_1 = x_2 = \cdots \) and Theorem 4.2 holds for the trivial choice \(r_{-} = 0\).
Suppose \(\epsilon _0 > 0\). For \(\epsilon _0 m \le 1/2\), Theorem 4.2 shows the existence of a root \(u_h\) to \(N_h\) in \(\overline{B(x_1,r_-)}\) that is the only root in \(\overline{B(x_h,\rho )}\). This, \( \Vert x_1-x_h\Vert _{X_h} \le \epsilon _0\), with \(\epsilon _0\) from (4.1), for the Newton correction \(x_1-x_h\) in the second inequality of (4.2), and triangle inequalities result in
This proves the existence of a discrete solution \(u_h\) in \( X_h\cap \overline{B(u,\epsilon _1)}\) as asserted in (i). Theorem 4.2 implies (ii).
Step 3 establishes the assertion (iii). Recall from Theorem 4.2 that the limit \(u_h\in \overline{B(x_1,r_-)}\) in (i)-(ii) is the only discrete solution in \(\overline{B(x_h,\rho )}\). Suppose there exists a second solution \({{\widetilde{u}}}_h\in X_h\cap \overline{B(u,\epsilon _1)}\) to \(N_h({{{{\widetilde{u}}}_h}})=0\). Since \(u_h\) is unique in \(\overline{B(x_h,\rho )}\), \({{\widetilde{u}}}_h\) lies outside \(\overline{B(x_h,\rho )}\). This and a triangle inequality show
with \(2m\epsilon _1 \le 1\) in the last step. This contradiction concludes the proof of (iii). \(\square \)
Remark 4.3
(error estimate) Recall \(\delta _4\) from (H4) and \(\epsilon _0\) from (4.1). An algebraic manipulation in (4.7) reveals, for \(\epsilon _0 m \le 1/2\), that
In the applications of Sects. 8-9, this leads to the energy norm estimate.
Remark 4.4
(estimate on \(\epsilon _1\)) In the applications, (4.1) leads to \(\epsilon _0 \lesssim \delta _3+\delta _4\). This, the definition of \(\epsilon _1\) in Theorem 4.1, (4.7), and Remark 4.3 provide \(\epsilon _1 \lesssim \delta _3+\delta _4\).
5 A priori error control
This section is devoted to a quasi-best approximation up to perturbations (B). Recall that the bounded bilinear form \(a: X \times Y \rightarrow {{\mathbb {R}}}\) satisfies (2.1), the trilinear form \(\Gamma : X \times X \times Y \rightarrow {{\mathbb {R}}}\) is bounded, and \(F \in Y^{*}\). The assumptions on the discretization with \(a_h: X_h \times Y_h \rightarrow {{\mathbb {R}}}\) with non-trivial finite-dimensional spaces \(X_h\) and \(Y_h\) of the same dimension \(\text {dim}(X_h) = \text {dim}(Y_h) \in {{\mathbb {N}}}\) are encoded in the stability and quasi-optimality. The stability of \(a_h\) and (2.2) mean \(\alpha _{0} > 0\) and the quasi-optimality assumes \(P \in L(X_h; X)\) with (2.3), \(R \in L(X_h; {\widehat{X}})\) with (2.5), \(S \in L(Y_h; {\widehat{Y}})\) , and \(Q \in L(Y_h; Y)\) (in this section, (2.4) and (2.6) are not employed). Recall \(\beta _1\) and \(\epsilon _1\) from (3.6) and Theorem 4.1.
Theorem 5.1
(a priori error control) Let \(u \in X\) be a regular root to (3.3), let \(u_h \in X_h\) solve (3.5), and suppose (H1), (2.2)-(2.3), (2.5), \(\Vert u - u_h\Vert _{{\widehat{X}}} \le \epsilon _2{{:}{=}}\min \left\{ \epsilon _1, \frac{ \kappa \beta _1}{ (1+ \Lambda _{\textrm{R}})^2\Vert S\Vert \Vert {{\widehat{\Gamma }}}\Vert } \right\} \), and \(0< \kappa <1\). Then
holds for \(C_{\textrm{qo}} = C_\textrm{qo}'{\beta ^{-1}_1(1-\kappa )^{-1}}(\beta _1 + 2 (1+\Lambda _{\textrm{R}}) \Vert S\Vert \Vert {{\widehat{\Gamma }}}\Vert \Vert u\Vert _X )\) with \(C_{\textrm{qo}}'{{:}{=}} 1 + \alpha _0^{-1}(\Lambda _{1} \Lambda _{\textrm{P}} + \Vert Q^*A\Vert (1 + \Lambda _{\textrm{P}}))\).
The theorem establishes a quasi-best approximation result (1.1) for \(S=Q\). The proof utilizes a quasi-best approximation result from [11] for linear problems.
Lemma 5.2
(quasi-best approximation for linear problem [11]) If \(u^*\in X\) and \(G(\bullet )=a(u^*,\bullet ) \in Y^*\), \(u_h^*\in X_h\) and \(a_h(u_h^*,\bullet ) =G(Q \bullet )\in Y_h^*\), then (2.2)-(2.3) and (H1) imply
Proof
This is indicated in [11, Theorem 5.4.a] for Hilbert spaces and we give the proof for completeness. For any \(x_h \in X_h\), the inf-sup condition (2.2) leads for \(e_h{{:}{=}}x_h-u_h^* \in X_h\) to some \(\Vert y_h\Vert _{Y_h} \le 1\) such that
Since \(a_h(u_h^*, y_h)= G(Qy_h)=a(u^*, Qy_h)\), this implies
with (H1), the operator norm \(\Vert Q^*A\Vert \) of \(Q^*A=a(\bullet , Q\bullet )\), and \(\Vert y_h\Vert _{Y_h} \le 1\) in the last step. Recall (2.3) and \(\Vert u^*-Px_h\Vert _X \le (1+\Lambda _{\textrm{P}}) \Vert u^*-x_h\Vert _{{\widehat{X}}} \) from (2.10) to deduce
This and a triangle inequality \(\Vert u^*-u_h^*\Vert _{{\widehat{X}}} \le \Vert e_h\Vert _{X_h} +\Vert u^*-x_h\Vert _{{\widehat{X}}}\) conclude the proof. \(\square \)
Proof of Theorem 5.1
Given a regular root \(u \in X\) to (3.3), \(G(\bullet ) {{:}{=}} F(\bullet ) - \Gamma (u,u,\bullet ) \in Y^*\) is an appropriate right-hand side in the problem \(a(u,\bullet ) = G(\bullet )\) with a discrete solution \(u_{h}^*\in X_h\) to \(a_h(u_{h}^*,\bullet ) = G(Q\bullet )\) in \(Y_h\). Lemma 5.2 implies (5.1) with \(u^*\) substituted by u, namely
Given the discrete solution \(u_h \in X_h\) to (3.5) and the approximation \(u_{h}^*\in X_h\) from above, let \(e_h {{:}{=}} u_{h}^*- u_h \in X_h\). The stability of the discrete problem from Theorem 2.1 leads to the existence of some \(y_h \in Y_h\) with norm \(\Vert y_h\Vert _{Y_h} \le 1/\beta _h\) for \(\beta _h \ge \beta _{0}\) from (2.9) and
with (3.2) in the last step. The definition of \(u_h^*\), G, and (3.5) show
The combination of the two previous displayed identities and elementary algebra show that
with the boundedness of \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\) and \(\Vert y_h\Vert _{Y_h} \le 1/\beta _h\) in the last step. This, \(\Vert u - Ru_h \Vert _{{\widehat{X}}} \le (1 + \Lambda _{\textrm{R}})\Vert u - u_{h} \Vert _{{\widehat{X}}}\) (resp. \(\Vert u - Ru_h^* \Vert _{{\widehat{X}}} \le (1 + \Lambda _{\textrm{R}})\Vert u - u_{h}^* \Vert _{{\widehat{X}}}\)) from (2.10), \(\beta _1 \le \beta _h\), and a triangle inequality show
Recall the assumption on \(\Vert u-u_h\Vert _{{\widehat{X}}} \le \epsilon _2\) to absorb the last term and obtain
This, the definition of \(\epsilon _2\), and (5.2) conclude the proof. \(\square \)
Remark 5.3
(estimate on \(\epsilon _2\)) The assumption of Theorem 5.1 and Remark 4.4 reveal \(\epsilon _2 \le \epsilon _1\lesssim \delta _3+\delta _4\) for the applications of Sects. 8, 9.
6 Goal-oriented error control
This section proves an a priori error estimate in weaker Sobolev norms based on a duality argument. Suppose Y is reflexive throughout this section so that, given any \(G \in X^{*}\), there exists a unique solution \(z \in Y\) to the dual linearised problem
Recall N from (3.1), A and B from Table 2 with (3.2), P, Q, R, and S with (2.3)–(2.6), and (\(\widehat{{\textbf {H1}}}\)) from Sect. 3. Since \(u \in X\) is a regular root, the derivative \(A+B \in {L(X;Y^*)}\) of N evaluated at u is a bijection and so is its dual operator \(A^*+B^* \in L(Y; X^*)\).
Theorem 6.1
(goal-oriented error control) Let \(u \in X\) be a regular root to (3.3) and let \(u_{h} \in X_h\) (resp. \(z \in Y\)) solve (3.5) (resp. (6.1)). Suppose (\(\widehat{{\textbf {H1}}}\)) and (2.3)–(2.6). Then, any \(G \in X^{*}\) and any \(z_h \in Y_h\) satisfy
with the weights
Proof
Since \(z \in Y\) solves (6.1), elementary algebra with (3.3), (3.5), and any \(z_h \in Y_h\) lead to
The first term \( (a+b)(u-Pu_h,z-Qz_h)\) on the right-hand side of (6.3) is bounded by
with (2.10)–(2.11) in the last step. The hypothesis (\(\widehat{{\textbf {H1}}}\)) controls the third term on the right-hand side of (6.3), namely
Elementary algebra with (3.2) shows that the remaining terms \({{\widehat{\Gamma }}}(Ru_h,Ru_h,Sz_h)-\Gamma (u,u,Qz_h)+b(u-Pu_h,Qz_h) \) on the right-hand side of (6.3) can be re-written as
Elementary algebra with the first term on the right-hand side of (6.4) reveals
The boundedness of \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\), (2.4), (2.6), and (2.10) show
The boundedness of \({\Gamma }(\bullet ,\bullet ,\bullet )\) and (2.10) lead to
A combination of the above estimates of the terms in (6.3) concludes the proof. \(\square \)
An abstract a priori estimate for error control in weaker Sobolev norms concludes this section.
Theorem 6.2
(a priori error estimate in weaker Sobolev norms) Let \(X_{\textrm{s}}\) be a Hilbert space with \(X + X_h \subset X_{\textrm{s}}\). Under the assumptions of Theorem 6.1, any \(z_h \in Y_h\) satisfies
Proof
Given \(u - Pu_h \in X \subset X_{\textrm{s}}\), a corollary of the Hahn-Banach extension theorem leads to some \(G \in X_{\textrm{s}}^*\subset X^*\) with norm \(\Vert G\Vert _{X_{\textrm{s}}^*} \le 1\) in \(X_\textrm{s}^*\) and \( G(u - Pu_h) = \Vert u - Pu_h \Vert _{X_{\textrm{s}}} \) [4]. This, a triangle inequality, and Theorem 6.1 conclude the proof. \(\square \)
7 Auxiliary results for applications
7.1 General notation
Standard notation of Lebesgue and Sobolev spaces, their norms, and \(L^2\) scalar products applies throughout the paper such as the abbreviation \(\Vert \bullet \Vert \) for \(\Vert \bullet \Vert _{L^2(\Omega )}\). For real s, \(H^s(\Omega )\) denotes the Sobolev space endowed with the Sobolev-Slobodeckii semi-norm (resp. norm) \(|\bullet |_{H^{\varvec{s}}(\Omega )}\) (resp. \(\Vert \bullet \Vert _{H^{\varvec{s}}(\Omega )}\) ) [20]; \(H^s(K){{:}{=}} H^s(\textrm{int}(K))\) abbreviates the Sobolev space with respect to the interior \(\textrm{int}(K)\ne \emptyset \) of a triangle K. The closure of \(D(\Omega )\) in \(H^s(\Omega )\) is denoted by \(H^s_0(\Omega )\) and \(H^{-s}(\Omega )\) is the dual of \(H^s_0(\Omega )\). The semi-norm and norm in \(W^{s,p} (\Omega )\), \(1 \le p \le \infty \), are denoted by \(|\bullet |_{W^{s,p}(\Omega )}\) and \(\Vert \bullet \Vert _{W^{s,p}(\Omega )}\). The Hilbert space \(V {{:}{=}} H_0^2(\Omega )\) is endowed with the energy norm \(\displaystyle |\!|\!|\bullet |\!|\!|{{:}{=}} |\bullet |_{H^2(\Omega )}\). The product space \(H^s(\Omega ) \times H^s(\Omega )\) (resp. \(L^p(\Omega ) \times L^p(\Omega )\)) is denoted by \(\textbf{H}^s(\Omega )\) (resp. \(\textbf{L}^p(\Omega )\)) and \(\textbf{V} =: V \times V\). The energy norm in the product space \(\textbf{H}^2(\Omega )\) is also denoted by \(|\!|\!|\bullet |\!|\!|\) and is \((|\!|\!|\varphi _1 |\!|\!|^2+|\!|\!|\varphi _2|\!|\!|^2)^{1/2}\) for all \(\Phi =(\varphi _1,\varphi _2)\in \textbf{H}^2(\Omega )\). The norm on \(\textbf{W}^{s,p}(\Omega )\) is denoted by \(\Vert \bullet \Vert _{\textbf{W}^{s,p}(\Omega )}\). Given any function \(v \in L^2(\omega )\), define the integral mean  ; where \(|\omega |\) denotes the area of \(\omega \). The notation \(A \lesssim B\) (resp. \(A \gtrsim B\)) abbreviates \(A \le CB\) (resp. \(A \ge CB\)) for some positive generic constant C, which depends exclusively on \(\Omega \) and the shape regularity of a triangulation \({\mathcal {T}}\); \(A\approx B\) abbreviates \(A\lesssim B \lesssim A\).
; where \(|\omega |\) denotes the area of \(\omega \). The notation \(A \lesssim B\) (resp. \(A \gtrsim B\)) abbreviates \(A \le CB\) (resp. \(A \ge CB\)) for some positive generic constant C, which depends exclusively on \(\Omega \) and the shape regularity of a triangulation \({\mathcal {T}}\); \(A\approx B\) abbreviates \(A\lesssim B \lesssim A\).
Triangulation. Let \({{\mathcal {T}}}\) denote a shape regular triangulation of the polygonal Lipschitz domain \(\Omega \) with boundary \(\partial \Omega \) into compact triangles and \({{\mathbb {T}}}(\delta )\) be a set of uniformly shape-regular triangulations \({\mathcal {T}}\) with maximal mesh-size smaller than or equal to \(\delta >0\). Given \({\mathcal {T}}\in {{\mathbb {T}}}\), define the piecewise constant mesh function \(h_{{\mathcal {T}}}(x)=h_K=\textrm{diam} (K)\) for all \(x \in K \in {\mathcal {T}}\), and set \(h_{\textrm{max}} {{:}{=}}\max _{K\in {\mathcal {T}}}h_K\). The set of all interior vertices (resp. boundary vertices) of the triangulation \({\mathcal {T}}\) is denoted by \({{\mathcal {V}}}(\Omega )\) (resp. \({{\mathcal {V}}}(\partial \Omega )\)) and \({{\mathcal {V}}} {{:}{=}} {{\mathcal {V}}}(\Omega ) \cup {{\mathcal {V}}}(\partial \Omega )\). Let \({\mathcal {E}}(\Omega )\) (resp. \({\mathcal {E}}(\partial \Omega )\)) denote the set of all interior edges (resp. boundary edges) in \({\mathcal {T}}\). Define a piecewise constant edge-function on \({\mathcal {E}}{{:}{=}}{\mathcal {E}}(\Omega )\cup {\mathcal {E}}(\partial \Omega )\) by \(h_{{\mathcal {E}}}|_E=h_E=\textrm{diam}(E)\) for any \(E\in {\mathcal {E}}\). For a positive integer m, define the Hilbert (resp. Banach) space \(H^m({\mathcal {T}}) \equiv \prod \nolimits _{K \in {\mathcal {T}}} H^m(K)\) (resp. \(W^{m,p}({\mathcal {T}}) \equiv \prod \nolimits _{K \in {\mathcal {T}}} W^{m,p}(K)) \). The triple norm \(|\!|\!|\bullet |\!|\!|{{:}{=}}|\bullet |_{H^{m}(\Omega )}\) is the energy norm and \(|\!|\!|\bullet |\!|\!|_{\text {pw}}{{:}{=}}|\bullet |_{H^{m}({\mathcal {T}})}{{:}{=}}\Vert D^m_\text {pw}\bullet \Vert \) is its piecewise version with the piecewise partial derivatives \(D_\text {pw}^m\) of order \(m\in {{\mathbb {N}}}\). For \(1<s<2\), the piecewise Sobolev space \(H^s({\mathcal {T}})\) is the product space \(\prod _{T\in {\mathcal {T}}} H^s(T)\) defined as \( \{ v_{\textrm{pw}} \in L^2(\Omega ): \forall T\in {\mathcal {T}}, v_{\textrm{pw}}|_T\in H^s(T)\}\) and is equipped with the Euclid norm of those contributions \( \Vert \bullet \Vert _{H^s(T)}\) for all \(T\in {\mathcal {T}}\). For \({{s}}=1 +\nu \) with \(0<\nu <1\), the 2D Sobolev-Slobodeckii norm [20] of \(f \in H^s(\Omega )\) reads \(\Vert f\Vert _{H^{\varvec{s}}(\Omega )}^2{{:}{=}} \Vert f\Vert _{H^{1}(\Omega )}^2+ |f|_{H^{\nu }(\Omega )}^2\) and
The piecewise version of the energy norm in \(H^2({\mathcal {T}})\) reads \(|\!|\!|\bullet |\!|\!|_{\text {pw}}{{:}{=}}|\bullet |_{H^{2}({\mathcal {T}})}{{:}{=}}\Vert D^2_\text {pw}\bullet \Vert \) with the piecewise Hessian \(D_\text {pw}^2\). The curl of a scalar function v is defined by \(\textrm{Curl}~v =\big (-\partial v /\partial y ,-\partial v /\partial x \big )^T\) and its piecewise version is denoted by \(\textrm{Curl }_{\textrm{pw}}\). The seminorm (resp. norm) in \(W^{m,p}({\mathcal {T}})\) is denoted by \(|\bullet |_{W^{m,p}({\mathcal {T}})}\) (resp. \(\Vert \bullet \Vert _{W^{m,p}({\mathcal {T}})}\)). Define the jump  and the average \(\langle \varphi \rangle _E{{:}{=}}\frac{1}{2}\left( \varphi |_{K_+}+\varphi |_{K_-}\right) \) across the interior edge E of \(\varphi \in H^1({\mathcal {T}})\) of the adjacent triangles \(K_+\) and \(K_-\). Extend the definition of the jump and the average to an edge on boundary by
and the average \(\langle \varphi \rangle _E{{:}{=}}\frac{1}{2}\left( \varphi |_{K_+}+\varphi |_{K_-}\right) \) across the interior edge E of \(\varphi \in H^1({\mathcal {T}})\) of the adjacent triangles \(K_+\) and \(K_-\). Extend the definition of the jump and the average to an edge on boundary by  and \(\langle \varphi \rangle _E{{:}{=}}\varphi |_E\) for \(E\in {\mathcal {E}}(\partial \Omega )\). For any vector function, the jump and the average are understood component-wise. Let \(\Pi _k\) denote the \(L^2(\Omega )\) orthogonal projection onto the piecewise polynomials \(\displaystyle P_k({\mathcal {T}}){{:}{=}}\left\{ v \in L^2(\Omega ): \forall \,K \in {\mathcal {T}}, v|_{K}\in P_k(K) \right\} \) of degree at most \(k \in {{\mathbb {N}}}_0\). (The notation \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\), \(\Pi _K\), and \(V_h\) below hides the dependence on \({\mathcal {T}}\in {{\mathbb {T}}}\).)
and \(\langle \varphi \rangle _E{{:}{=}}\varphi |_E\) for \(E\in {\mathcal {E}}(\partial \Omega )\). For any vector function, the jump and the average are understood component-wise. Let \(\Pi _k\) denote the \(L^2(\Omega )\) orthogonal projection onto the piecewise polynomials \(\displaystyle P_k({\mathcal {T}}){{:}{=}}\left\{ v \in L^2(\Omega ): \forall \,K \in {\mathcal {T}}, v|_{K}\in P_k(K) \right\} \) of degree at most \(k \in {{\mathbb {N}}}_0\). (The notation \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\), \(\Pi _K\), and \(V_h\) below hides the dependence on \({\mathcal {T}}\in {{\mathbb {T}}}\).)
7.2 Finite element function spaces and discrete norms
This section introduces the discrete spaces and norms for the Morley/dG/\(C^0\)IP/WOPSIP schemes. The Morley finite element space [15] reads
The semi-scalar product \(a_{\textrm{pw}}\) is defined by the piecewise Hessian \(D^2_{\textrm{pw}}\), for all \(v_{\textrm{pw}}, w_{\textrm{pw}} \in H^2({\mathcal {T}})\) as
The bilinear form \(a_{\textrm{pw}}(\bullet ,\bullet )\) induces a piecewise \(H^2\) seminorm \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} = a_\textrm{pw}(\bullet ,\bullet )^{1/2}\) that is a norm on \(V+\text {M}({\mathcal {T}})\) [10]. The piecewise Hilbert space \( H^2({\mathcal {T}})\) is endowed with a norm \(\Vert \bullet \Vert _h\) [7] defined by

with the jumps  for \(z \in {{\mathcal {V}}}(\partial \Omega )\); the edge-patch \(\omega (E){{:}{=}}\text { int}(K_+\cup K_-)\) of the interior edge \(E=\partial K_+\cap \partial K_-\in {{\,\mathrm{{\mathcal {E}}}\,}}(\Omega )\) is the interior of the union \(K_+\cup K_-\) of the neighboring triangles \(K_+\) and \(K_-\), and
for \(z \in {{\mathcal {V}}}(\partial \Omega )\); the edge-patch \(\omega (E){{:}{=}}\text { int}(K_+\cup K_-)\) of the interior edge \(E=\partial K_+\cap \partial K_-\in {{\,\mathrm{{\mathcal {E}}}\,}}(\Omega )\) is the interior of the union \(K_+\cup K_-\) of the neighboring triangles \(K_+\) and \(K_-\), and  for \(E \in {{\mathcal {E}}}(\partial \Omega )\) at the boundary with jump partner zero owing to the homogeneous boundary conditions.
for \(E \in {{\mathcal {E}}}(\partial \Omega )\) at the boundary with jump partner zero owing to the homogeneous boundary conditions.
For all \(v_{\textrm{pw}}, w_{\textrm{pw}} \in H^2({\mathcal {T}})\) and parameters \(\sigma _1,\sigma _2>0\) (that will be chosen sufficiently large but fixed in applications), define \(c_\textrm{dG}(\bullet , \bullet )\) and the mesh dependent dG norm \(\Vert \bullet \Vert _{\textrm{dG}}\) by

The discrete space for the \(C^0\)IP scheme is \(S^2_0({\mathcal {T}}) {{:}{=}} P_2({\mathcal {T}}) \cap H^1_0(\Omega )\). The restriction of \(\Vert \bullet \Vert _{\textrm{dG}}\) to \(H^1_0(\Omega )\) with a stabilisation parameter \(\sigma _{\textrm{IP}}>0\) defines the norm for the \(C^0\)IP scheme below,

For all \(v_{\textrm{pw}}, w_{\textrm{pw}} \in H^2({\mathcal {T}})\), the WOPSIP norm \(\Vert \bullet \Vert _{\textrm{P}}\) is defined by

The discrete space for dG/WOPSIP schemes is \(P_2({\mathcal {T}})\). The discrete norms \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\), \(\Vert \bullet \Vert _{\textrm{dG}}\) and \( \Vert \bullet \Vert _{\textrm{IP}}\) are all equivalent to \(\Vert \bullet \Vert _{h}\) on \(V+V_h\) for \(V_h \in \{ \text {M}({\mathcal {T}}), P_2({\mathcal {T}}),S^2_0({\mathcal {T}}) \}\). In comparison to \(j_h(\bullet )\), the jump contribution in \(\Vert \bullet \Vert _{\textrm{P}}\) involves smaller negative powers of the mesh-size and so \(j_h(v_{\textrm{pw}})^2 \lesssim c_\textrm{P}(v_{\textrm{pw}},v_{\textrm{pw}})\) (with \(h_E \le \textrm{diam}(\Omega ) \lesssim 1\)); but there is no equivalence of \(\Vert \bullet \Vert _h\) with \(\Vert \bullet \Vert _{\textrm{P}}\) in \(V+P_2({\mathcal {T}})\).
Lemma 7.1
(Equivalence of norms [11, Remark 9.2]) It holds \(\Vert \bullet \Vert _{h} = |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) on \(V + \textrm{M}({\mathcal {T}})\), \(\Vert \bullet \Vert _{h} \approx \Vert \bullet \Vert _{\textrm{dG}} { \lesssim \Vert \bullet \Vert _{\textrm{P}}}\) on \(V + P_2({\mathcal {T}})\), and \(\Vert \bullet \Vert _{h} \approx \Vert \bullet \Vert _{\textrm{IP}}\) on \(V + S^2_0({\mathcal {T}})\).
7.3 Interpolation and companion operators
The classical Morley interpolation operator \(I_\text {M}\) is generalized from \(H^2_0(\Omega )\) to the piecewise \(H^2\) functions by averaging in [11].
Definition 7.2
(Morley interpolation [11, Definition 3.5]) Given any \(v_{\textrm{pw}} \in H^2({\mathcal {T}})\), define \(I_{\textrm{M}}v_{\textrm{pw}} {{:}{=}} v_\textrm{M} \in \textrm{M}({\mathcal {T}})\) by the degrees of freedom as follows. For any interior vertex \(z \in {{\mathcal {V}}}({\mathcal {T}})\) with the set of attached triangles \({\mathcal {T}}(z)\) of cardinality \(|{\mathcal {T}}(z)| \in {{\mathbb {N}}}\) and for any interior edge \(E \in {{\mathcal {E}}}(\Omega )\) with a mean value operator \(\langle \bullet \rangle _{E}\) set

The remaining degrees of freedom at vertices and edges on the boundary are set zero owing to the homogeneous boundary conditions.
Lemma 7.3
(interpolation error estimates [11, Lemma 3.2, Theorem 4.3]) Any \(v_{\textrm{pw}} \in H^2({\mathcal {T}})\) and its Morley interpolation \(I_{\textrm{M}} v_{\textrm{pw}} \in \textrm{M}({\mathcal {T}})\) satisfy
-
(a)
\( \sum _{m=0}^2 | h_{{\mathcal {T}}}^{m-2} (v_{\textrm{pw}}- I_{\textrm{M}} v_{\textrm{pw}}) |_{H^m({\mathcal {T}})} \lesssim \Vert (1-\Pi _0)D^2_{\textrm{pw}} v_{\textrm{pw}}\Vert + j_h(v_{\textrm{pw}}) { \lesssim } \Vert v_{\textrm{pw}}\Vert _h;\)
-
(b)
\(\sum _{m=0}^2 |h_{{\mathcal {T}}}^{m-2} (v_{\textrm{pw}} - I_\textrm{M} v_{\textrm{pw}} )|_{H^m({\mathcal {T}})} \approx \min _{w_{\textrm{M}} \in \textrm{M}({\mathcal {T}})} \Vert v_{\textrm{pw}} - w_{\textrm{M}} \Vert _h \approx \min _{w_{\textrm{M}} \in \textrm{M}({\mathcal {T}})} \sum _{m=0}^2 |h_{{\mathcal {T}}}^{m-2} (v_{\textrm{pw}} - w_{\textrm{M}})|_{H^m({\mathcal {T}})};\)
-
(c)
the integral mean property of the Hessian, \(D^2_{\textrm{pw}} I_\textrm{M}=\Pi _0 D^2 \text { in } V;\)
-
(d)
\(|\!|\!|v- I_{\textrm{M}}v |\!|\!|_{\textrm{pw}} \lesssim h_{\textrm{max}}^{t-2} \Vert v \Vert _{H^{t}(\Omega )} \text { for all } v \in H^{t}(\Omega ) \text { with } 2 \le t \le 3.\)
Let \(HCT({\mathcal {T}})\) denote the Hsieh-Clough-Tocher finite element space [15, Chapter 6].
Lemma 7.4
(right-inverse [10, 11, 19]) There exists a linear map \(J:\textrm{M}({\mathcal {T}}) \rightarrow (HCT({\mathcal {T}}) + P_8({\mathcal {T}}))\cap H^2_0(\Omega )\) such that any \(v_{\textrm{M}} \in \textrm{M}({\mathcal {T}})\) and any \(v_2 \in P_2({\mathcal {T}}) \) satisfy (a)–(h).
-
(a)
\(Jv_{\textrm{M}}(z) {=}v_{\textrm{M}}(z)\) for any \(z \in {{\mathcal {V}}}\);
-
(b)
\(\nabla (Jv_{\textrm{M}})(z) = |{\mathcal {T}}(z)|^{-1} \sum _{K \in {\mathcal {T}}(z)}(\nabla v_{\textrm{M}} \vert _{K})(z)\) for \(z \in {{\mathcal {V}}}(\Omega )\);
-
(c)
 for any \(E \in {{\mathcal {E}}}\);
for any \(E \in {{\mathcal {E}}}\); -
(d)
\(v_{\textrm{M}} - J v_{\textrm{M}} \perp P_2({\mathcal {T}})\) in \(L^2(\Omega )\);
-
(e)
\({\sum _{m=0}^2 \Vert h_{{\mathcal {T}}}^{m-2} D_\textrm{pw}^m (v_{\textrm{M}} - J v_{\textrm{M}}) \Vert {\lesssim }\min _{v \in V} {|\!|\!|v_{\textrm{M}} - v |\!|\!|_{\textrm{pw}}}}\);
-
(f)
\( \Vert v_2 - JI_{\textrm{M}} v_2 \Vert _{H^t({\mathcal {T}})} \lesssim h_{\textrm{max}}^{2-t} \min _{v \in V} \Vert v_2 - v \Vert _h \text { holds for } 0\le t \le 2\);
-
(g)
\(\sum _{m=0}^{2} \Vert h_{\mathcal {T}}^{m-3} D^m_\textrm{pw}((1-I_\textrm{M}) v_2) \Vert + \sum _{m=0}^2 \Vert h_{{\mathcal {T}}}^{m-2} D^m_{\textrm{pw}}((1- J )I_{\textrm{M}}v_2)\Vert \lesssim \min _{v \in V} \Vert v-v_2\Vert _{\textrm{P}}\);
-
(h)
\( |v_2-JI_{\textrm{M}}v_2|_{W^{1,2/(1-t)}({\mathcal {T}})} \lesssim h_{\textrm{max}}^{1-t} \min _{v \in V}\Vert v-v_2\Vert _{h}\) holds for \(0<t<1\).
Proof of \({\varvec{(a)}}\)-\({\varvec{(f)}}\). This is included in [10, 19, 11, Lemma 3.7, Theorem 4.5]. \(\square \)
Proof of \({\varvec{(g)}}\). The inequality \(\sum _{m=0}^{2} \Vert h_{\mathcal {T}}^{m-3} D^m_\textrm{pw}((1-I_\text {M}) v_2) \Vert \lesssim \Vert v - v_2\Vert _{\textrm{P}}\) follows as in the proof of Lemma 10.2 in [11]. Lemma 7.4.e and a triangle inequality show
Since \( |\!|\!|I_{\textrm{M}} v_2 - v_2 |\!|\!|_{{\textrm{pw}}} \le h_\textrm{max} |\!|\!|h_{{\mathcal {T}}}^{-1} (I_{\textrm{M}} v_2 - v_2) |\!|\!|_{{\textrm{pw}}} \lesssim h_{\textrm{max}} \Vert v - v_2 \Vert _{\textrm{P}}\) from the first part of (g) with \(m=2\), the above displayed estimate, and \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _{\textrm{P}}\) conclude the proof of (g). \(\square \)
Proof of \({\varvec{(h)}}.\) An inverse estimate [17, Lemma 12.1], [2, Lemma 4.5.3], [15, Theorem 3.2.6] on each triangle \({\widehat{T}}\) in the HCT subtriangulation \({\widehat{{\mathcal {T}}}}\) of \({\mathcal {T}}\) in each component of \(g{{:}{=}}\nabla _{\textrm{pw}}(v_2-JI_{\textrm{M}}v_2)\) reads \(\Vert g\Vert _{L^{2/(1-t)}({\widehat{T}})} \le C_\textrm{inv}h_{{\widehat{T}}}^{-t}\Vert g\Vert _{L^2({\widehat{T}})}.\) Consequently,
with \(\Vert \bullet \Vert _{\ell ^{2/(1-t)}} \le \Vert \bullet \Vert _{\ell ^2}\) in the sequence space \({\mathbb {R}}^{{\mathbb {N}}}\) (\(\ell ^p\) is decreasing in \(p \ge 1\)) in the last step. With the shape regularity \(h_{{\widehat{{\mathcal {T}}}}} \approx h_{{\mathcal {T}}}\), this reads
Since \(I_{\textrm{M}}(v_2-JI_{\textrm{M}}v_2)=0\) by Lemma 7.4, Lemma 7.3.a provides
Since \(j_h(JI_{\textrm{M}}v_2)=0=j_h(v)\), the definition of \(j_h(\bullet )\) shows \(j_h(v_2-JI_{\textrm{M}}v_2)=j_h(v_2-v)\). This, the definition of \(\Vert \bullet \Vert _h\) in (7.2), and Lemma 7.4.f imply
The combination of (7.7)–(7.9) implies the assertion. \(\square \)
Remark 7.5
(orthogonality of J) Since J is a right-inverse of \(I_\text {M}\), i.e., \(I_\text {M}J=\textrm{id}\) in \(\text {M}({\mathcal {T}})\) [11, (3.9)], the integral mean property of the Hessian from Lemma 7.3.c reveals \(a_{\textrm{pw}}(v_2, (1-J)v_\text {M}) = a_{\textrm{pw}} (v_2, (1-I_\text {M})Jv_\text {M})=0\) for any \(v_2 \in P_2({\mathcal {T}})\) and \(v_\text {M}\in \text {M}({\mathcal {T}})\).
Lemma 7.6
(an intermediate bound) For \(1<p<\infty \), any \((v_2 ,v)\in P_2({\mathcal {T}}) \times V\) satisfies \(|v+v_2|_{W^{1,p}({\mathcal {T}})}\) \( \lesssim \Vert v+v_2\Vert _h.\)
Proof
The triangle inequality \(|v+v_2|_{W^{1,p}({\mathcal {T}})} \le |v+J I_\text {M}v_2|_{W^{1,p}(\Omega )} + |v_2-JI_\text {M}v_2|_{W^{1,p}({\mathcal {T}})} \) and the Sobolev embedding \(H^2_0(\Omega ) \hookrightarrow W^{1,p}_0(\Omega )\) in 2D lead to
with \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _h\) and Lemma 7.4.f in the last step. The inequality \(|v_2-JI_\text {M}v_2|_{W^{1,p}({\mathcal {T}})} \le |\Omega |^{1/p} |v_2 - J I_\text {M}v_2|_{W^{1,\infty }({\mathcal {T}})}\) leads to some \(K \in {\mathcal {T}}\) with \( |v_2 - J I_\text {M}v_2|_{W^{1,\infty }({\mathcal {T}})} = |v_2 - JI_\text {M}v_2|_{W^{1,\infty }(K)}\). The inverse estimate \( |v_2 - JI_\text {M}v_2|_{W^{1,\infty }(K)} \lesssim h_K^{-1} |v_2 - JI_\text {M}v_2|_{H^1(K)}\) and Lemma 7.4.f reveal \(|v_2 - J I_\text {M}v_2|_{W^{1,\infty }({\mathcal {T}})} \lesssim \Vert v+v_2\Vert _h\). The combination of the above inequalities concludes the proof. \(\square \)
Lemma 7.7
(quasi-optimal smoother R) Any \(R \in \{\text {id}, I_{\textrm{M}}, JI_{\textrm{M}}\}\) and \({\widehat{V}} =V+V_h\) with
satisfy
The constant \(\Lambda _{\textrm{R}}\) exclusively depends on the shape regularity of \({\mathcal {T}}\).
Proof for \(R = \text {id}.\) This holds with \(\Lambda _{\textrm{R}}=0\). \(\square \)
Proof for \(R = I_{\textrm{M}}.\) Since \(\Vert (1-\Pi _0)D^2_{\textrm{pw}} v_{h}\Vert =0 \) for \(v_h \in V_h \subseteq P_2({\mathcal {T}})\), Lemma 7.3.a leads to \(|\!|\!|(1-I_{\textrm{M}})v_h |\!|\!|_{\textrm{pw}}\lesssim j_h(v_h)\). This, the definition of \(\Vert \bullet \Vert _h\), and \(j_h(I_{\text {M}}v_h) =0=j_h(v)\) show
with Lemma 7.1 in the last step. Theorem 4.1 of [11] provides \(\Vert (1- I_\textrm{M})v_h \Vert _{{\widehat{V}}} \lesssim \Vert (1-I_{\textrm{M}})v_h \Vert _h\) for the dG/\(C^0\)IP norm \(\Vert \bullet \Vert _{{\widehat{V}}}\). The combination proves the assertion for Morley/dG/\(C^0\)IP.
For WOPSIP, the definition of \(\Vert \bullet \Vert _{\textrm{P}}\) in (7.6), \(|\!|\!|(1-I_{\textrm{M}})v_h |\!|\!|_\textrm{pw}\lesssim \Vert v - v_h \Vert _{\textrm{P}}\) from the displayed inequality above, and \(c_{\textrm{P}}(v,v)=c_{\textrm{P}}(v,v_h)=0\) reveal
Proof for \(R = JI_{\textrm{M}}.\) Triangle inequalities and \(\Vert \bullet \Vert _{{\widehat{V}}}=|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \) in V show
Lemma 7.4.f and Lemma 7.1 conclude the proof for \(R=JI_\text {M}\). \(\square \)
The transfer from \(\text {M}({\mathcal {T}})\) into \(V_h\) [11] is modeled by some linear map \(I_h: \text {M}({\mathcal {T}}) \rightarrow V_h\) that is bounded in the sense that there exists some constant \(\Lambda _h \ge 0\) such that \( \Vert v_{\textrm{M}} - I_h v_\textrm{M}\Vert _h \le \Lambda _h |\!|\!|v_{\textrm{M}} - v |\!|\!|_{\textrm{pw}}\) holds for all \(v_\text {M}\in \text {M}({\mathcal {T}})\) and all \(v \in V\). A precise definition of \(I_h= I_{\textrm{C}} I_\text {M}\) concludes this section.
Definition 7.8
(transfer operator [11, (8.4)]) For \(v_{\textrm{M}} \in \textrm{M}({\mathcal {T}})\), let \(I_{\textrm{C}} : \textrm{M}({\mathcal {T}}) \rightarrow S^2_0({\mathcal {T}})\) be defined by
followed by Lagrange interpolation in \(P_2(K)\) for all \(K \in {\mathcal {T}}\).
Remark 7.9
(approximation) A triangle inequality with \(I_\text {M}v\), Lemma 7.1, and \(\Vert v_{\textrm{M}} - I_{\textrm{C}} v_{\textrm{M}} \Vert _h \lesssim |\!|\!|v- v_{\textrm{M}} |\!|\!|_{\textrm{pw}}\) for any \(v \in V\) and \(v_{\textrm{M}} \in \textrm{M}({\mathcal {T}})\) from [11, (5.11)] show \(\Vert v - I_\textrm{C}I_{\textrm{M}}v \Vert _h \lesssim |\!|\!|v- I_\text {M}v |\!|\!|_{\textrm{pw}}\). In particular, given any \(v \in V\) and given any positive \(\epsilon >0\), there exists \(\delta >0\) such that for any triangulation \({\mathcal {T}}\in {{\mathbb {T}}}(\delta )\) with discrete space \(V_h\), we have \(\Vert v-v_h\Vert _{{\widehat{V}}} <\epsilon \) for some \(v_h \in V_h\). (The proof utilizes the density of smooth functions in V, the preceding estimates, and Lemma 7.3.)
8 Application to Navier-Stokes equations
This section verifies the hypotheses (H1)–(H4) and (\(\widehat{{\textbf {H1}}}\)) and establishes (A)-(C) for the 2D Navier-Stokes equations in the stream function vorticity formulation. Sections 8.1 and 8.2 describe the problem and four quadratic discretizations. The a priori error control for the Morley/dG/\(C^0\)IP (resp. WOPSIP) schemes follows in Sects. 8.3–8.6 (resp. Sect. 8.7) .
8.1 Stream function vorticity formulation of Navier-Stokes equations
The stream function vorticity formulation of the incompressible 2D Navier–Stokes equations in a bounded polygonal Lipschitz domain \(\Omega \subset {\mathbb {R}}^2\) seeks \(u \in H^2_0(\Omega )=:V=X=Y\) such that
for a given right-hand side \(F \in V^*\). The biharmonic operator \(\Delta ^2\) is defined by \(\Delta ^2\phi {{:}{=}}\phi _{xxxx}+\phi _{yyyy}+2\phi _{xxyy}\). The analysis of extreme viscosities lies beyond the scope of this article, and the viscosity in (8.1) is set one.
For all \(\phi ,\) \(\chi ,\psi \in V\), define the bilinear and trilinear forms \(a(\bullet , \bullet )\) and \(\Gamma (\bullet ,\bullet ,\bullet )\) by
The weak formulation that corresponds to (8.1) seeks \(u \in V\) such that
8.2 Four quadratic discretizations
This subsection presents four lowest-order discretizations, namely, the Morley/dG/\(C^0\)IP/ WOPSIP schemes for (8.3). Define the discrete bilinear forms
with \(a_{\textrm{pw}}\) from (7.1) and \( {\textsf {b}}_h, {{\textsf {c}}}_h \) in Table 3 for the four discretizations. Let \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet ){{:}{=}}\Gamma _\textrm{pw}(\bullet ,\bullet ,\bullet )\) be the piecewise trilinear form defined for all \(\phi , \chi , \psi \in H^2({\mathcal {T}})\) by
For all the four discretizations of Table 3, recall \({\widehat{b}}(\bullet ,\bullet ) {{:}{=}} \Gamma _{\textrm{pw}}(u,\bullet ,\bullet ) + \Gamma _{\textrm{pw}}(\bullet ,u,\bullet ): (V+P_2({\mathcal {T}})) \times (V+P_2({\mathcal {T}})) \rightarrow {{\mathbb {R}}}\) from (3.2). Given \(R,S \in \{\textrm{id}, I_\text {M}, JI_\text {M}\} \), the discrete schemes for (8.3) seek a solution \(u_h\in V_h\) to
8.3 Main results
This subsection states the results on the a priori control for the discrete schemes of Sect. 8.2. Lemma 7.1 shows that \(\Vert \bullet \Vert _{{\widehat{V}}} \approx \Vert \bullet \Vert _h\) for the Morley/dG/\(C^0\)IP schemes. The WOPSIP scheme is discussed in Sect. 8.7. Unless stated otherwise, \(R \in \{\textrm{id}, I_\text {M}, JI_\text {M}\}\) is arbitrary.
Theorem 8.1
(a priori energy norm error control) Given a regular root \(u \in V=H^2_0(\Omega )\) to (8.3) with \(F \in H^{-2}(\Omega )\) and \(0<t<1\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(u_h \in V_h\) to (8.5) with \(\Vert u-u_h\Vert _{{h}} \le \epsilon \) for the Morley/dG/\(C^0\)IP schemes satisfies
If \(F \in H^{-r}(\Omega )\) for some \(r<2\), then (8.6) holds with \(t=0\).
Remark 8.2
(quasi best-approximation) The best approximation result (1.1) holds for \({S=Q=J I_\text {M}}\).
A comparison result follows as in [11, Theorem 9.1] and the proof is therefore omitted.
Theorem 8.3
(comparison for \(R \in \{ \textrm{id}, I_\textrm{M}, JI_\textrm{M} \}\)and \(S=Q=JI_\textrm{M}\)) The regular root \(u \in V\) to (8.3) and for \(h_\textrm{max}\) sufficiently small, the respective local discrete solution \(u_\textrm{M}, u_{\textrm{dG}}, u_{\textrm{IP}} \in V_h\) to (8.5) for the Morley/dG/\(C^0\)IP schemes with \(S=J I_\textrm{M}\) satisfy
A summary of the a priori error control in Theorem 8.5 below is
with \(a,b, C_b\) as described in Table 4.
Remark 8.4
(Table 1vs 4) Note that the parameter \(t>0\) appears in Table 4 and not in Table 1. For \(r=2\), (8.7) solely asserts \(\Vert u-u_h\Vert _{H^s({\mathcal {T}})}\lesssim \Vert u-u_h\Vert _h^2 \lesssim 1\) even though a and b depend on t.
Recall the index of elliptic regularity \(\sigma _{\textrm{reg}}\) and \(\sigma {{:}{=}}\min \{\sigma _{\textrm{reg}},1\}>0\) from Section 1.
Theorem 8.5
(a priori error control in weaker Sobolev norms) Given a regular root \(u \in V\) to (8.3) with \(F \in H^{-2}(\Omega )\), \(2-\sigma \le s <2\), and \(0<t<1\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(u_h \in V_h\) to (8.5) with \(\Vert u-u_h\Vert _{{\widehat{V}}} \le \epsilon \) satisfies (a)–(e).
(a) For the Morley/dG/\(C^0\)IP schemes with \(R{{:}{=}}J I_\textrm{M},\)
(b) For the Morley/dG/\(C^0\)IP schemes with \(R{{:}{=}} I_\textrm{M}\) and (c) for the Morley scheme with \(R=\textrm{id}\),
(d) For \(\sigma < 1 \), whence \(1<s<2\), for the Morley/dG/\(C^0\)IP schemes with \(R \in \{ I_\textrm{M}, JI_\textrm{M} \}\) and for the Morley scheme with \(R= \textrm{id}\),
(e) If \(F \in H^{-r}(\Omega )\) for some \( r<2\), then (a)-(c) hold with \(t=0\).
Remark 8.6
(constant dependency) The constants hidden in the notation \(\lesssim \) of Theorem 8.1 (resp. 8.5) exclusively depend on the exact solution u (resp. u and z) to (8.3) (resp. (8.3) and (6.1)), shape regularity of \(\,\,{{\mathcal {T}}},\) t (resp. s, t), and on respective stabilisation parameters \({\sigma _1, \sigma _2, \sigma _{\textrm{IP}}\approx 1}\).
Remark 8.7
(scaling for WOPSIP) The semi-scalar product \({{\textsf {c}}}_h(\bullet ,\bullet )\) in the WOPSIP scheme is an analog to the one in \(j_h\) from (7.2) with different powers of the mesh-size. It is a consequence of the different scaling of the norms that (H1) and (\(\widehat{{\textbf {H1}}}\)) do not hold for the WOPSIP scheme.
8.4 Preliminaries
This section investigates the piecewise trilinear form \(\Gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) from (8.4) and its boundedness with a global parameter \(0<t<1 \) that may be small. Recall the energy norm \(|\!|\!|\bullet |\!|\!|\), and the discrete norms \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\), \(\Vert \bullet \Vert _h\), and \(\Vert \bullet \Vert _{\textrm{P}}\) from Sect. 7.2. The constants hidden in the notation \(\lesssim \) in Lemma 8.8 below exclusively depend on the shape regularity of \({\mathcal {T}}\) and on t.
Lemma 8.8
(boundedness of the trilinear form) Any \(\psi \in V\) and any \({\widehat{\phi }}, {\widehat{\chi }}, {\widehat{\psi }} \in V+P_2({\mathcal {T}})\), satisfy
Proof
A general Hölder inequality reveals
(owing to \(t/2 +(1-t)/2=1/2\) and \(|\Delta _{\textrm{pw}} {\widehat{\phi }}| \le \sqrt{2} |D^2_{\textrm{pw}} {\widehat{\phi }}| \) a.e.). Lemma 7.6 provides \(| {\widehat{\chi }} |_{W^{1,2/t}({\mathcal {T}})} \lesssim \Vert {\widehat{\chi }}\Vert _h\) and \(| {\widehat{\psi }} |_{W^{1,2/(1-t)}({\mathcal {T}})} \lesssim \Vert {\widehat{\psi }}\Vert _h\). The combination with (8.8) concludes the proof of (a). For \(\psi \in V\) (replacing \({\widehat{\psi }}\)), the Sobolev embedding \(H^{t}(\Omega )\hookrightarrow L^{2/(1-t)}(\Omega )\) [4, Corollary 9.15] provides
The combination with (8.8) concludes the proof of (b). \(\square \)
Lemma 8.9
(approximation properties) For all \(t>0\), there exists a constant \(C(t)>0\) such that any \(\phi , \chi \in V\cap H^{2+t}(\Omega )\), \({\widehat{\phi }}, {\widehat{\chi }} \in V+P_2({\mathcal {T}})\), and \((v,v_2,v_{\textrm{M}})\in V \times P_2({\mathcal {T}})\times \textrm{M}{({\mathcal {T}})}\) satisfy
- (a):
-
\( \Gamma _{\textrm{pw}}( {\widehat{\phi }},{\widehat{\chi }}, (1-JI_{\textrm{M}})v_2) \le C(t) h_{\max }^{1-t}|\!|\!|{\widehat{\phi }} |\!|\!|_{\textrm{pw}} \Vert {\widehat{\chi }} \Vert _{h} \Vert v-v_2\Vert _{h}, \)
- (b):
-
\( \Gamma _{\textrm{pw}}( {\widehat{\phi }},{\chi }, (1-JI_{\textrm{M}})v_2) \le C(t) h_{\max }|\!|\!|{\widehat{\phi }} |\!|\!|_{\textrm{pw}} \Vert {\chi } \Vert _{H^{2+t}(\Omega )} \Vert v-v_2\Vert _{h}, \)
- (c):
-
\(\Gamma _{\textrm{pw}}(( 1- J)v_{\textrm{M}},{\widehat{\phi }},{\widehat{\chi }}) \le {} C(t) h_{\max }^{1-t} |\!|\!|v-v_\textrm{M}|\!|\!|_{\textrm{pw}}\Vert {\widehat{\phi }}\Vert _h \Vert {\widehat{\chi }}\Vert _h .\)
- (d):
-
\(\Gamma _{\textrm{pw}}(( 1- J)v_{\textrm{M}},{\phi },{\chi }) \le {} C(t) h_{\max }|\!|\!|v-v_\textrm{M}|\!|\!|_{\textrm{pw}}\Vert {\phi }\Vert _{H^{2+t}(\Omega )} \Vert {\chi }\Vert _{H^{2+t}(\Omega )} .\)
Proof of \({\varvec{(a)}}.\) Lemma 7.6 and 7.4.h establish \(|{\widehat{\chi }} |_{W^{1,2/t}({\mathcal {T}})} \lesssim \Vert {\widehat{\chi }}\Vert _h\) and \(| (1-JI_{\textrm{M}})v_2 |_{W^{1,2/(1-t)}({\mathcal {T}})}\lesssim h_{\max }^{1-t}\Vert v-v_2\Vert _{h}.\) The combination with (8.8) concludes the proof of (a). \(\square \)
Proof of \({\varvec{(b)}}.\) A generalised Hölder inequality and the embedding \(H^{2+t}(\Omega )\hookrightarrow W^{1,\infty }(\Omega )\) [4, Corollary 9.15] provide
Lemma 7.4.f controls the last factor and concludes the proof of (b). \(\square \)
Proof of \({\varvec{(c)}}.\) Lemma 7.3.c implies \(\int _\Omega \Delta _{\textrm{pw}}(v_{\textrm{M}}-J v_{\textrm{M}}) \Pi _0 D_{\textrm{pw}}{\widehat{\phi }}\cdot \Pi _0 \textrm{Curl}_{\textrm{pw}}{\widehat{\chi }} \mathrm{\,dx}=0\) and so
A generalised Hölder inequality shows
Abbreviate \(a_T{{:}{=}}h_T^{2-t}\Vert \Delta (v_{\textrm{M}}-Jv_{\textrm{M}})\Vert _{L^\infty (T)}\) for a triangle \(T \in {\mathcal {T}}\) with area \(|T| \le h_T^2\) to establish
with the monotone decreasing \(\ell ^p\) norm for \(2\le 2/(1-t)\) in the last step. An inverse estimate (with respect to the HCT refinement \({\widehat{{\mathcal {T}}}}\) of \({\mathcal {T}}\)) as in the proof of Lemma 7.4.h provides \(\Vert \Delta ((1-J)v_{\textrm{M}})\Vert _{L^\infty (T)} \le \sqrt{2} \Vert v_{\textrm{M}}-Jv_{\textrm{M}} \Vert _{W^{2,\infty }(\Omega )}\lesssim h_{T}^{-1}\Vert v_{\textrm{M}}-Jv_{\textrm{M}} \Vert _{H^2(T)}.\) Hence \(a_T \lesssim h_{T}^{1-t}\Vert v_{\textrm{M}}-Jv_{\textrm{M}} \Vert _{H^2(T)}\) and
A piecewise Poincaré inequality with Payne-Weinberger constant \(h_{T}/\pi \) [24] reads
Recall \(|{\widehat{\chi }} |_{W^{1,2/t}({\mathcal {T}})}\lesssim \Vert {\widehat{\chi }}\Vert _h\) from the proof of (a). The combination of the previous estimates of the three terms in (8.10) proves the asserted estimate for the first integral in the right-hand side of (8.9). The analysis for the second term is rather analogue (interchange the role of \({\widehat{\phi }}\) and \({\widehat{\chi }}\)). Notice that (c) follows even in the form \(\Gamma _{\textrm{pw}}(( 1- J)v_{\textrm{M}},{\widehat{\phi }},{\widehat{\chi }}) \le {} C(t) h_{\max }^{1-t} |\!|\!|v-v_\text {M}|\!|\!|_{\textrm{pw}}(|\!|\!|{\widehat{\phi }}|\!|\!|_{\textrm{pw}} \Vert {\widehat{\chi }}\Vert _h+\Vert {\widehat{\phi }}\Vert _h |\!|\!|{\widehat{\chi }}|\!|\!|_{\textrm{pw}}).\) \(\square \)
Proof of \({\varvec{(d)}}.\) Substitute \(\phi \equiv {\widehat{\phi }}\), \(\chi \equiv {\widehat{\chi }}\) in (8.9) (with \(\phi ,\chi \in V\cap H^{2+t}(\Omega )\)) and employ a different generalised Hölder inequality for the first term to infer
The remaining arguments of the proof of (c) simplify to \(\Vert \Delta _{\textrm{pw}}(1-J) v_{\textrm{M}} \Vert _{L^{2}(\Omega )} \le \sqrt{2} |\!|\!|(1-J) v_{\textrm{M}} |\!|\!|_{\textrm{pw}}\), \(\pi \Vert (1-\Pi _0 )D{\phi }\Vert _{L^2(\Omega )} \le h_{\max }|\!|\!|\phi |\!|\!|\), and \(|{\chi } |_{W^{1,\infty }(\Omega )} \lesssim \Vert \chi \Vert _{H^{2+t}(\Omega )}\) (by embedding \(H^{2+t}(\Omega )\hookrightarrow W^{1,\infty }(\Omega )\) for \(t>0\)). The resulting estimate
and Lemma 7.4.e lead to the assertion for one term in the right-hand side of (8.9). The analysis of the other term is analog. Notice that (d) follows even in the form \(\Gamma _{\textrm{pw}}(( 1- J)v_{\textrm{M}},{\phi },{\chi }) \le {} C(t) h_{\max }|\!|\!|v-v_\text {M}|\!|\!|_{\textrm{pw}}(|\!|\!|{\phi }|\!|\!|\Vert {\chi }\Vert _{H^{2+t}(\Omega )}+\Vert {\phi }\Vert _{H^{2+t}(\Omega )} |\!|\!|{\chi }|\!|\!|).\) \(\square \)
8.5 Proof of Theorem 8.1
The conditions in Theorem 5.1 are verified to establish the energy norm estimates. The hypotheses (2.3)–(2.6) follow from Lemma 7.7. Hypothesis (H1) is verified for Morley/dG/\(C^0\)IP in the norm \(\Vert \bullet \Vert _h\) in [11, Lemma 6.6] and this norm is equivalent to \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \),\(\Vert \bullet \Vert _{\textrm{dG}}\), and \(\Vert \bullet \Vert _{\textrm{IP}}\) by Lemma 7.1.
Recall \(a(\bullet ,\bullet )\) and \(\Gamma (\bullet ,\bullet ,\bullet )\) from (8.2), \({{\widehat{\Gamma }}}(\bullet ,\bullet ,\bullet )\equiv {\Gamma }_{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) from (8.4), and \({\widehat{b}}(\bullet ,\bullet )\) from (3.2) for the regular root \(u \in H^2_0(\Omega )\). For \(\theta _h \in V_h\) with \(\Vert \theta _{h}\Vert _{h} = 1\), Lemma 8.8.b, and \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _h \) provide \({\widehat{b}}(R\theta _h,\bullet ) \in H^{-1-t}(\Omega )\) for \(R \in \{ \textrm{id}, I_\text {M}, JI_\text {M}\}\). There exists a unique \(\xi \equiv \xi (\theta _h) \in V\cap H^{3-t}(\Omega )\) such that \(a(\xi ,\phi ) = {\widehat{b}}(R\theta _h,\phi )\) for all \(\phi \in V\) and \(\Vert \xi \Vert _{H^{3-t}(\Omega )} \lesssim \Vert {\widehat{b}}(R\theta _h,\bullet )\Vert _{H^{-1-t}(\Omega )}\lesssim 1\). The last inequality follows from Lemma 8.8.b and the boundedness of \(R \in \{\textrm{id}, I_\text {M}, JI_\text {M}\}\) from Lemma 7.7. Since \(I_h=\textrm{id}\) (resp. \(I_h=I_{\textrm{C}}\)) for Morley/dG (resp. \(C^0\)IP), Lemma 7.1 (resp. Remark 7.9) and Lemma 7.3.d establish (H2) with \(\delta _{2} = \sup \{ \Vert \xi - I_h I_{\text {M}} \xi \Vert _{h}: \theta _h\in V_h, \Vert \theta _h\Vert _{h}=1 \}\lesssim h_{\textrm{max}}^{1-t}\).
Since \(\delta _3=0\) for \(Q=S=JI_{\text {M}}\) it remains \(S=\textrm{id}\) and \(S=I_{\textrm{M}}\) in the sequel to establish (H3). Given \(\theta _h\) and \(y_h\) in \(V_h=X_h=Y_h\) of norm one, define \(v_2{{:}{=}}Sy_h \in P_2({\mathcal {T}})\) and observe \(Qy_h=JI_{\textrm{M}}y_h=JI_{\textrm{M}}v_2\) (by \(S=\textrm{id},I_{\textrm{M}}\)). Hence with the definition of \({\widehat{b}}(\bullet ,\bullet )\) from (3.2), Lemma 8.9.a shows
The boundedness of R and \(I_{\textrm{M}}\) and the equivalence of norms show \(\Vert R\theta _h\Vert _h\Vert v_2\Vert _h \lesssim 1\) and so \(\delta _{3} \lesssim h_{\textrm{max}}^{1-t}\).
Consequently, for the three schemes under question and for a sufficiently small mesh-size \(h_{\max }\), (2.9) holds with \(\beta _h\ge \beta _0 \gtrsim 1\).
For \(u \in H^2_0(\Omega )\) and \(\epsilon >0\), Remark 7.9 establishes (H4) with \(\delta _4 < \epsilon \) for all the three schemes. The existence and uniqueness of a discrete solution \(u_h\) then follows from Theorem 4.1.
For the Morley/dG/\(C^0\)IP schemes with \(F \in H^{-2}(\Omega )\), Lemma 8.9.a with \(v=0\) for \(S=\textrm{id}\) resp. \(S=I_{\textrm{M}}\), \(\Vert \bullet \Vert _h\approx \Vert \bullet \Vert _{V_h}\) on \(V_h\), and the boundedness of \(I_\text {M}\) show
The energy norm error control then follows from Theorem 5.1.
For \(F \in H^{-r}(\Omega )\) with \(r<2\), the energy norm error estimate (8.6) with \(t=0\) can be established by replacing Lemma 8.9.a in the above analysis for \(r=2\) by Lemma 8.9.b.\(\square \)
8.6 Proof of Theorem 8.5
This subsection establishes the a priori control in weaker Sobolev norms for the Morley/dG/\(C^0\)IP schemes of Sect. 8.2. Given \(2-\sigma \le s \le 2\), and \(G \in H^{-s}(\Omega )\) with \(\Vert G\Vert _{H^{-s}(\Omega )}=1\), the solution z to the dual problem (6.1) belongs to \( V \cap H^{4-s}(\Omega )\) by elliptic regularity. This and Lemma 7.3.d provide
The assumptions in Theorem 6.2 with \(X_{s}{{:}{=}} H^{s}({\mathcal {T}})\) and \(z_h {{:}{=}} I_h I_{\textrm{M}}z\) are verified to establish Theorem 8.5.a-e. The control of the linear terms in Theorem 6.2 is identical for the parts (a)-(e) and this is discussed first. The proof starts with a triangle inequality
in the norm \({H^s({\mathcal {T}})}=\prod _{T\in {\mathcal {T}}} H^s(T)\). The Sobolev-Slobodeckii semi-norm over \(\Omega \) involves double integrals over \(\Omega \times \Omega \) and so is larger than or equal to the sum of the contributions over \(T\times T\) for all the triangles \(T\in {\mathcal {T}}\), i.e., \( \sum _{T\in {\mathcal {T}}} |\bullet |_{H^s(T)}^2\le |\bullet |_{H^s(\Omega )}^2\) for any \(1<s<2\). The definition of \(\Vert \bullet \Vert _{H^{s}({\mathcal {T}})}\) for \(1<s<2\), Lemma 7.4.f with \(t=1\) and \(P=JI_{\textrm{M}}\) establish
The formal equivalence of the Sobolev-Slobodeckii norm and the norm by interpolation of Sobolev spaces provides for \(g{{:}{=}}\nabla _{\textrm{pw}}(Pu_h-u_h)\), \(\theta {{:}{=}}s-1\) and \(K \in {\mathcal {T}}\) that
The point is that a scaling argument reveals \(C(K,\theta )=C(\theta )\approx 1\) is independent of \(K \in {\mathcal {T}}\) [10]. The Young’s inequality \(\big (ab\le {a^p}/{p}+{b^q}/{q}\text { for }a,b \ge 0, {1}/{p}+{1}/{q}=1\big )\) leads (for \(a=h_K^{2\theta (\theta -1)}\Vert g\Vert _{L^2(K)}^{2(1-\theta )} \), \(b= h_K^{2\theta (1-\theta )}|g|_{H^1(K)}^{2\theta }\), \(p={1}/({1-\theta })\), and \(q={1}/{\theta }\)) to
Since \(P=JI_{\text {M}}\) and \(g=\nabla _{\textrm{pw}}(Pu_h-u_h)\), the estimates (7.8)–(7.9) with \(t=\theta \) show \(\Vert h_{{\mathcal {T}}}^{-\theta }g\Vert ^2_{L^2(\Omega )} \lesssim h_{\textrm{max}}^{1-\theta }\Vert u- u_h\Vert _h.\) This and Lemma 7.4.f for \(t=2\) provide
The combination of (8.15)–(8.17) reveals \(|\nabla _{\textrm{pw}}(Pu_h-u_h)|_{H^{s-1}({\mathcal {T}})} \lesssim h_{\textrm{max}}^{2-s}\Vert u-u_h\Vert _h\) and, with (8.14),
This leads to the assertion for one term on the right-hand side of (8.13). To estimate the second term, \(\Vert u-Pu_h\Vert _{H^s({\mathcal {T}})}= G(u-Pu_h)\), we verify the assumptions in Theorem 6.1. The hypothesis (\(\widehat{{\textbf {H1}}}\)) for the Morley/dG/\(C^0\)IP schemes is derived in [11, Lemma 6.6] for an equivalent norm (by Lemma 7.1) and Lemma 7.7 for \(R=JI_\text {M}\). The conditions (2.3)–(2.6) also follow from Lemma 7.7 as stated in the proof of Theorem 8.1. Hence, Theorem 6.1 applies and provides
Since \(\Vert \bullet \Vert _{\textrm{dG}} \approx |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \(V+\text {M}({\mathcal {T}})\) (by Lemma 7.1), (8.12) establishes
for the Morley/dG schemes with \(I_h=\textrm{id}\). Remark 7.9 and (8.12) establish (8.20) for the \(C^0\)IP scheme. The combination of (8.19)–(8.20) reads
The combination of (8.13), (8.18), and (8.21) verifies, for each of the Morley/dG/\(C^0\)IP schemes, that
Proof of Theorem 8.5.a
The difference \( {\Gamma }_{\textrm{pw}}(Ru_h,Ru_h,Qz_h) - \Gamma (Pu_h,Pu_h, Qz_h)\) vanishes for \(P=R=JI_\text {M}\) in each of the three schemes. The terms \( {\Gamma }_{\textrm{pw}}(u,u,(S-Q)z_h)\) in (8.22) are estimated below for \(S \in \{ \textrm{id}, I_{\textrm{M}}, JI_{\textrm{M}}\}\) and \(F \in H^{-2}(\Omega )\). Note that \(Qz_h{{:}{=}}J z_h=J I_\text {M}z_h\) holds for the Morley scheme. For \(S =\textrm{id}\) and each of the three discretizations, Lemma 8.9.a with \(v_2=z_h\) provides
with (8.20) in the last step. For \(S = I_{\textrm{M}}\), Lemma 8.9.a with \(v_2 = I_{\textrm{M}}z_h\) and \(\Vert \bullet \Vert _{{\widehat{V}}} \approx \Vert \bullet \Vert _{h}\) reveal
A triangle inequality and Lemma 7.7 for \(R=I_\text {M}\) provide \(\Vert z- I_{\textrm{M}}z_h \Vert _{h} \le (1+\Lambda _{\textrm{R}}) \Vert z - z_h \Vert _{h} \lesssim h_{\textrm{max}}^{2-s}\) with (8.20) in the last step. Altogether, we obtain \(\Gamma _{\textrm{pw}}(u,u,(1 -J )I_{\textrm{M}}z_h) \lesssim h_{\textrm{max}}^{3-t-s} \). The aforementioned estimates and (8.22) conclude the proof. \(\square \)
Proof of Theorem 8.5.b
All the terms except the last two in (8.22) are already estimated in the proof of (a). For \(P=Q=JI_\text {M}\) and \(R=I_\text {M}\), elementary algebra reveals
The bound \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _{h}\), a triangle inequality, and Lemma 7.7 for \(R=I_\text {M}\) result in
as in Remark 2.8. This and Lemma 7.4.e prove
A triangle inequality and (8.24)–(8.25) imply
As in Remark 2.8, analogous arguments plus (8.20) provide
Lemma 8.9.c and the equivalence \(\Vert \bullet \Vert _h \approx |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \(V+\text {M}({\mathcal {T}})\) (by Lemma 7.1) control the first term on the right-hand side of (8.23), namely
The first factor is bounded in (8.24). Since the dual solution \(z \in V \cap H^{4-s}(\Omega )\) is bounded in \(V=H^2_0(\Omega )\) (even in \(H^{4-s}(\Omega )\)), (8.27) reveals \(|\!|\!|JI_{\textrm{M}}z_h |\!|\!|\lesssim 1.\) Since \(|\!|\!|I_{\textrm{M}}u_h |\!|\!|_{\textrm{pw}}\lesssim 1\) as well, we infer
The anti-symmetry of \(\Gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) with respect to the second and third variables allows the application of Lemma 8.9.a to the second term on the right-hand side of (8.23), namely
The last step employed (8.24) and the boundedness \(|\!|\!|JI_{\textrm{M}} u_h|\!|\!|+|\!|\!|JI_{\textrm{M}} z_h|\!|\!|\lesssim 1\) as well. The combination of the previously displayed estimate with (8.28) and (8.23) leads to
The estimates of \({\Gamma }_{\textrm{pw}}(u,u,(S-Q)z_h)\) from the above proof of Theorem 8.5.a, (8.29), and (8.22) conclude the proof.
Proof of Theorem 8.5.c
Since \(u_h= u_{\textrm{M}} = I_{\textrm{M}}u_{\textrm{M}}\), and \(P=Q=J\), for the Morley FEM, the difference \({\Gamma }_{\textrm{pw}}( u_\text {M}, u_\text {M},J I_\text {M}z_h) -{\Gamma }(J u_\text {M}, J u_\text {M}, J I_\text {M}z_h)\) is controlled by (8.29). This, (8.22), and the estimates from the above proof of Theorem 8.5.a conclude the proof. \(\square \)
Proof of Theorem 8.5.d
The choice \(t{{:}{=}}s-1>0\) in the estimates in (a)-(c) concludes the proof. \(\square \)
Proof of Theorem 8.5.e
For \(F \in H^{-r}(\Omega )\) with \(r<2\), the lower-order error estimates can be established with \(t=0\) by the substitution of the respective assertions of Lemma 8.9.a,c by Lemma 8.9.b,d. \(\square \)
Remark 8.10
(weaker Sobolev norm estimates with \(R=\textrm{id}\)) For the dG/\(C^0\)IP schemes, (8.23) involves in particular \(\Gamma _{\textrm{pw}} ((1-J I_\text {M})u_h,u_h,JI_{\textrm{M}}z_h) \) and improved estimates are unknown.
8.7 WOPSIP scheme
Recall \(a_h(\bullet ,\bullet ) = a_{\textrm{pw}}(\bullet ,\bullet ) + {{\textsf {c}}}_h(\bullet ,\bullet )\), \(P = Q = JI_{\textrm{M}}\) and \({{\textsf {c}}}_h(\bullet ,\bullet )\) from Table 3, \(a_{\textrm{pw}}(\bullet ,\bullet )\) from (7.1), and let \(u_h \equiv u_{\textrm{P}}\) in this subsection. The norm \(\Vert \bullet \Vert _{\textrm{P}}\) from (7.6) for the WOPSIP scheme is not equivalent to \(\Vert \bullet \Vert _h\) from (7.2) and hence (H1) and (\(\widehat{{\textbf {H1}}}\)) do not follow. This does not prevent rather analog a priori error estimates.
Theorem 8.11
(a priori WOPSIP) Given a regular root \(u \in V\) to (8.3) with \(F \in H^{-2}(\Omega )\), \(2-\sigma \le s<2\), and \(0<t<1\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(u_h \in V_h\) to (8.5) with \( \Vert u-u_h\Vert _{\textrm{P}} \le \epsilon \) for the WOPSIP scheme satisfies (a)–(e).
Moreover, if \(u \in V \cap H^{4-r}(\Omega )\) with \(F \in H^{-r}(\Omega )\) for \(2-\sigma \le r, s \le 2\), then
(d) For \(\sigma < 1 \), whence \(1<s<2\), and the WOPSIP scheme with \(R \in \{ I_\textrm{M}, JI_\textrm{M} \}\),
(e) If \(F \in H^{-r}(\Omega )\) for some \( r<2\), then (a)-(c) hold with \(t=0\).
The subsequent lemma extends (H1) in the analysis of the WOPSIP scheme.
Lemma 8.12
(variant of (H1)) There exists a constant \(\Lambda _{\textrm{W}}> 0\) such that any \(v \in V\) and \(v_2 \in P_2({\mathcal {T}})\) satisfy
Proof
Note that \({{\textsf {c}}}_{h}(I_{\textrm{M}}v,v_2) = 0\) for \(v \in V\) and \(v_2 \in P_2({\mathcal {T}})\) from Table 3 and the definition of \(\text {M}({\mathcal {T}})\). Utilize this in \(a_h(\bullet ,\bullet ) = a_{\textrm{pw}}(\bullet ,\bullet ) + {{\textsf {c}}}_h(\bullet ,\bullet )\) to infer
Lemma 7.3.c implies
Since \(a_{\textrm{pw}}((1 - I_{\textrm{M}})v,(1 - I_{\textrm{M}})v_2) = 0 = a_{\textrm{pw}}(I_{\textrm{M}}v,(1 - J)I_{\textrm{M}}v_2)\) from Lemma 7.3.c and Remark 7.5,
Since Lemma 7.4.g provides \(|\!|\!|h_{{\mathcal {T}}}^{-1} (1 - I_{\textrm{M}})v_2 |\!|\!|_{\textrm{pw}} + |\!|\!|(1 - J)I_{\textrm{M}}v_2 |\!|\!|_{\textrm{pw}} \lesssim \Vert v_2 \Vert _{\textrm{P}}\), this proves
The combination of (8.30)–(8.31) concludes the proof. \(\square \)
Proof of (H2)-(H4) for the WOPSIP scheme. For a regular root \(u \in V\) to (8.3) and any \(\theta _h \in P_2({\mathcal {T}})\) with \(\Vert \theta _{h}\Vert _{\textrm{P}} = 1\), Lemma 8.8.b, \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _{\textrm{P}}\), and Lemma 7.1 lead to \({\widehat{b}}(R\theta _h,\bullet ) \in H^{-1-t}(\Omega )\) for \(R\in \{\textrm{id}, I_\text {M}, J I_\text {M}\}\). Therefore, there exists a unique \(\xi \equiv \xi (\theta _h) \in V\cap H^{3-t}(\Omega )\) with \(\Vert \xi \Vert _{H^{3-t}(\Omega )} \lesssim 1\) such that \(a(\xi ,\phi ) = {\widehat{b}}(R\theta _h,\phi )\) for all \(\phi \in V\). Since \(I_h=\textrm{id}\) and \(\Vert \bullet \Vert _{\textrm{P}}=|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \(V+\text {M}({\mathcal {T}})\) from (7.6), Lemma 7.3.d leads to (H2) with \(\delta _{2} = \sup \{ \Vert \xi - I_hI_{\text {M}} \xi \Vert _{\textrm{P}}: \theta _h\in P_2({\mathcal {T}}), \Vert \theta _h\Vert _{\textrm{P}}=1\}\lesssim h_{\textrm{max}}^{1-t}\).
The proof of (H3) starts as in (8.11) and concludes \(\delta _3\lesssim h_{\textrm{max}}^{1-t}\) from \(\Vert \bullet \Vert _h \lesssim \Vert \bullet \Vert _{\textrm{P}}\) by Lemma 7.1.
The hypothesis (H4) with \(\delta _4 =\Vert u-x_h\Vert _{\textrm{P}} < \epsilon \) follows from Remark 7.9. \(\square \)
Proof of discrete inf-sup condition
The proof of \(\beta _0 \gtrsim 1\) in (2.9) follows also for the WOPSIP scheme the above lines until (2.17) with \(\xi {{:}{=}} A^{-1}({{\widehat{b}}}(Rx_h,\bullet )|_Y)\in X\). Recall that (2.2) leads to \(x_h +\xi _h \in P_2({\mathcal {T}})\) and then to some \(\phi _h \in P_2({\mathcal {T}})\) with \(\Vert \phi _h\Vert _{\textrm{P}}=1\) and \(\alpha _h \Vert x_h + \xi _h \Vert _{\textrm{P}} = a_{h}(x_h+\xi _h,\phi _h);\) this time \(\epsilon =0\) can be neglected. An alternative split reads
Lemma 8.12, \(\xi _h = I_{\textrm{M}}\xi \), and \(|\!|\!|(1 - I_{\textrm{M}}) \xi |\!|\!|_{\textrm{pw}} \lesssim \delta _2{\lesssim h_{\textrm{max}}^{1-t}}\) from (H2) provide
The arguments in (2.20) lead to \(a(\xi ,Q\phi _h) \le {{\widehat{b}}}(Rx_h,S\phi _h)+\delta _3\). The combination of this with (8.32)–(8.33) provides
Replace (2.21) by (8.34) and apply the arguments thereafter to establish the stability condition (2.9) with \(\beta _0 {{:} {=}} \alpha _h {{\widehat{\beta }}} - (\Lambda _{\textrm{W}}+ \alpha _h) \delta _2 - \delta _{3} - \Lambda _{\textrm{W}}|\!|\!|h_{{\mathcal {T}}} I_{\textrm{M}} \xi |\!|\!|_{\textrm{pw}}\) for some \(\Lambda _{\textrm{W}}\lesssim 1.\) \(\square \)
Proof of existence and uniqueness of the discrete solution
The analysis follows the proof of Theorem 4.1 verbatim until (4.6). Instead of (H1), Lemma 8.12 and \(x_h = I_{\textrm{M}}u\) in (H4) control the first two terms on the right-hand side of (4.6), namely
The remaining steps follow those of the proof of Theorem 4.1 with (4.1) replaced by
\(\square \)
Proof of Theorem 8.11.a
Recall from Lemma 5.2 that \(u^*\in X\) and \(G(\bullet )=a(u^*,\bullet ) \in Y^*\), \(u_h^*\in X_h\) and \(a_h(u_h^*,\bullet ) =G(Q \bullet )\in Y_h^*\). In the proof of Lemma 5.2, set \(x_h {{:}{=}} I_{\textrm{M}}u^*\) so that Lemma 8.12 implies
Therefore, \(u^*\) and \(u_ h^*\) in Lemma 5.2 satisfy \(\Vert u^*- u_h^*\Vert _{\textrm{P}} \le C_{\textrm{qo}}' |\!|\!|u^*- I_{\textrm{M}} u^*|\!|\!|_{\textrm{pw}} +\alpha _0^{-1} \Lambda _{\textrm{W}}|\!|\!|h_{{\mathcal {T}}} I_{\textrm{M}} u^*|\!|\!|_{\textrm{pw}}\) for \(C_{\textrm{qo}}' = 1 + \alpha _0^{-1} \Lambda _{\textrm{W}}\).
The hypotheses (2.3)–(2.6) follow from Lemma 7.7; (H2)-(H4) are already verified. The error estimate in Lemma 5.2 applies to Theorem 5.1 with \(x_{h} = I_{\textrm{M}}u\) and \(\Vert \bullet \Vert _{\textrm{P}} = |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \(V + \text {M}({\mathcal {T}})\) and establishes
For \(u \in V\), the last displayed estimate, Lemma 8.9.a with \(v=0\) for \(S=\textrm{id}\) (resp. with \(v_2 \in \text {M}({\mathcal {T}})\) for \(S=I_{\textrm{M}}\)), Lemma 7.1, and the boundedness of \(I_{\textrm{M}}\) conclude the proof. \(\square \)
Proof of Theorem 8.11.b
A triangle inequality leads to
with \(G(u-Pu_h)=\Vert u-Pu_h\Vert _{H^s({\mathcal {T}})}\)owing to a corollary of the Hahn-Banach theorem as in the proof of Theorem 6.2 in the last step. Since \(z \in Y\) solves (6.1), elementary algebra with (3.3)–(3.5) and \(z_h {{:}{=}} I_{\textrm{M}}z \in Y_h\) lead to an alternative identity in place of (6.3), namely
with \(a_h(u_h,z_h) = a_{\textrm{pw}}(u_h,z)\) from Lemma 7.3.c in the last step. Since \(a_{\textrm{pw}}(I_{\textrm{M}}u, z- Qz_h) = 0\) from Lemma 7.3.c and Remark 7.5,
with boundedness of \(a_{\textrm{pw}}(\bullet ,\bullet )\) and (2.11) in the last step. A triangle inequality shows that
with \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _{\textrm{P}}\), \(\Vert (1- I_{\textrm{M}})u_h \Vert _{\textrm{P}} \le \Lambda _{\textrm{R}}\Vert u - u_h \Vert _{\textrm{P}}\) from Lemma 7.7, and \(|\!|\!|I_{\textrm{M}}(u - u_h) |\!|\!|_{\textrm{pw}} \le |\!|\!|u - u_h |\!|\!|_{\textrm{pw}}\) in the last step. Arguments analogous to (8.31) and Lemma 7.4.g with \(v = u\) lead to
The combination of (8.36)–(8.38) and the estimates for the remaining terms in the right-hand side of (8.36) from the last part (after (6.4)) of the proof of Theorem 6.1 result in
Since \(z_h=I_{\text {M}}z\), Lemma 7.3.d provides \(|\!|\!|z-z_h|\!|\!|_{\textrm{pw}} \lesssim h_{\max }^{2-s}\) and \(|\!|\!|h_{{\mathcal {T}}} z_h |\!|\!|_{\textrm{pw}} \lesssim h_{\max }\). Lemma 7.4.f and \(\Vert \bullet \Vert _h \lesssim \Vert \bullet \Vert _{\textrm{P}}\) (by Lemma 7.1) establish \(\Vert Pu_h -u_h\Vert _{H^s({\mathcal {T}})}\lesssim h_{\max }^{2-s}\Vert u-u_{\textrm{P}}\Vert _{\textrm{P}}.\) The combination of those estimates with (8.35) and (8.39) reveals
The last three terms in the above inequality can be estimated as in the proof of Theorem 8.5.a with \(\Vert \bullet \Vert _h \lesssim \Vert \bullet \Vert _{\textrm{P}}\) (by Lemma 7.1) and this concludes the proof. \(\square \)
Proof of Theorem 8.11.c
The arguments in (b) and Theorem 8.5.b establish (c). \(\square \)
Proof of Theorem 8.11.d
The choice \(t{{:}{=}}s-1\) in (b)-(c) concludes the proof. \(\square \)
Proof of Theorem 8.11.e
For \(F \in H^{-r}(\Omega )\) with \(r<2\), the a priori error estimates can be established with \(t=0\) by a substitution of the assertions in Lemma 8.9.a,c by Lemma 8.9.b,d.
9 Application to von Kármán equations
This section verifies (H1)-(H4) and (\(\widehat{{\textbf {H1}}}\)), and establishes (A)-(C) for the von Kármán equations. Sects. 9.1 and 9.2 present the problem and four discretizations; the a priori error control for the Morley/dG/\(C^0\)IP/WOPSIP schemes follows in Sect. 9.3–9.6.
9.1 Von Kármán equations
The von Kármán equations in a polygonal domain \(\Omega \subset {{\mathbb {R}}}^2\) seek \((u,v) \in H^2_0(\Omega ) \times H^2_0(\Omega ) = V \times V =: {{\textbf {V}}}\) such that
The von Kármán bracket \([\bullet ,\bullet ]\) above is defined by \(\displaystyle [\eta ,\chi ]{{:}{=}}\eta _{xx}\chi _{yy}+\eta _{yy}\chi _{xx}-2\eta _{xy}\chi _{xy}\) for all \(\eta ,\chi \in V\). The weak formulation of (9.1) seeks \(u,v\in V \) that satisfy for all \((\varphi _{1},\varphi _{2}) \in {\textbf {V}}\)
with \(\displaystyle \gamma (\eta ,\chi ,\varphi ){{:}{=}}-\frac{1}{2}\int _\Omega [\eta ,\chi ]\varphi \mathrm{\,dx}\text { for all } \eta ,\chi , \varphi \in V\) and \(a(\bullet ,\bullet )\) from (8.2).
For all \(\Xi =(\xi _1,\xi _2),\Theta =(\theta _1,\theta _2),\) and \(\Phi =(\varphi _1,\varphi _2)\in {\textbf {V}}\), define the forms
Then the vectorised formulation of (9.2) seeks \(\Psi =(u,v)\in {\textbf {V}}\) such that
The trilinear form \(\Gamma (\bullet ,\bullet ,\bullet )\) inherits symmetry in the first two variables from \(\gamma (\bullet ,\bullet ,\bullet )\). The following boundedness and ellipticity properties hold [5, 16, 22]
9.2 Four quadratic discretizations
This subsection presents the Morley/dG/\(C^0\)IP/WOPSIP schemes for (9.3). The spaces and operators employed in the analysis of the von Kármán equations given in Table 5 are vectorised versions (denoted in boldface) of those presented in Table 3, e.g., \({\varvec{I}}_{\textrm{M}} = I_{\textrm{M}} \times I_{\textrm{M}} \). Recall \(a_{\textrm{pw}}(\bullet ,\bullet )\) from (7.1) and define the bilinear form \(a_h : ({\textbf {V}}_h + {{\textbf {M}}}({\mathcal {T}})) \times ({\textbf {V}}_h + {{\textbf {M}}}({\mathcal {T}})) \rightarrow {{\mathbb {R}}}\) by
The definitions of \( \textsf {b}_h\) and \(\textsf {c}_h\) for the Morley/dG/\(C^0\)IP/WOPSIP schemes from Table 3 are omitted in Table 5 for brevity. For all \(\eta , \chi , \varphi \in H^2({\mathcal {T}}),\) let \(\gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) be the piecewise trilinear form defined by
and, for all \(\Xi =(\xi _1,\xi _2),\Theta =(\theta _1,\theta _2), \Phi =(\varphi _1,\varphi _2) \in \textbf{H}^{2}({\mathcal {T}})\), let
For all the schemes and a regular root \(\Psi \in {{\textbf {V}}}\) to (9.3), let \({\widehat{b}}(\bullet ,\bullet ) {{:}{=}} 2\Gamma _{\textrm{pw}}(\Psi ,\bullet ,\bullet )\) in (3.2). For \(R, S \in \{{{{\textbf {i}}}}{{{\textbf {d}}}}, {\varvec{I}}_{\textrm{M}}, {{\varvec{J}}}{{\varvec{I}}}_{\textrm{M}} \}\), the discrete scheme seeks a root \({\varvec{\Psi }}_{h} {{:}{=}} (u_{h},v_{h})\in {\textbf {V}}_h\) to
9.3 Main results
The main results on a priori error control in energy and weaker Sobolev norms for the Morley/dG/\(C^0\)IP/ WOPSIP schemes of Sect. 9.2 are stated in this and verified in the subsequent subsections. Unless stated otherwise, \(R \in \{{{{\textbf {i}}}}{{{\textbf {d}}}}, {\varvec{I}}_\text {M}, {{\varvec{J}}}{{\varvec{I}}}_\text {M}\}\) is arbitrary.
Theorem 9.1
(A priori energy norm error control) Given a regular root \(\Psi \in \textbf{V}\) to (9.3) with \(F \in \textbf{H}^{-2}(\Omega )\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(\Psi _h \in \textbf{V}_h\) to (9.5) with \(\Vert \Psi -\Psi _h\Vert _{h} \le \epsilon \) for the Morley/dG/\(C^0\)IP schemes satisfies
The a priori estimates in Table 1 hold for von Kármán equations component-wise for \({F} \in \textbf{H}^{-r}(\Omega )\), \(2 - \sigma \le r \le 2\) and \(\Psi \in {\textbf {V}} \cap \textbf{H}^{4-r}(\Omega )\).
Remark 9.2
(Comparison) Suppose \(\Psi \in {{\textbf {V}}}\) is a regular root to (9.3) with \({F} \in \textbf{H}^{-2}(\Omega )\) and \(S= {{\varvec{J}}} {\varvec{I}}_\text {M}\). If \(h_{\textrm{max}}\) is sufficiently small, then the respective local discrete solutions \(\Psi _\text {M}, \Psi _{\textrm{dG}}, \Psi _{\textrm{IP}} \in {{\textbf {V}}}_h\) to (9.5) for the Morley/dG/\(C^0\)IP schemes satisfy
Theorem 9.3
(a priori error control in weaker norms) Given a regular root \(\Psi \in \textbf{V}\cap \textbf{H}^{4-r}(\Omega )\) to (9.3) with \({F} \in \textbf{H}^{-r}(\Omega )\) for \(2-\sigma \le r,s \le 2\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(\Psi _h \in \textbf{V}_h\) to (9.5) with \(\Vert \Psi -\Psi _h\Vert _{h} \le \epsilon \) satisfies
(a) for the Morley/dG/\(C^0\)IP schemes and \(R =\{{{\varvec{J}}} {\varvec{I}}_\textrm{M}, {\varvec{I}}_\textrm{M}\}\) and (b) for the Morley scheme and \(R = \textbf{id}.\)
Theorem 9.4
(a priori WOPSIP) Given a regular root \(\Psi \in \textbf{V}\) to (9.3) with \({F} \in \textbf{H}^{-2}(\Omega )\), there exist \(\epsilon , \delta > 0\) such that, for any \(\displaystyle {\mathcal {T}}\in {\mathbb {T}}(\delta )\), the unique discrete solution \(\Psi _h \in \textbf{V}_h\) to (9.5) with \(\Vert \Psi -\Psi _h\Vert _{\textrm{P}} \le \epsilon \) for the WOPSIP scheme satisfies
Moreover, if \({F} \in \textbf{H}^{-r}(\Omega )\) for \(2-\sigma \le r,s\le 2\) and \(R\in \{{{\varvec{J}}} {\varvec{I}}_\textrm{M}, {\varvec{I}}_\textrm{M}\}\), then
9.4 Preliminaries
Two lemmas on the trilinear form \(\Gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) from (9.4) are crucial for the a priori error control.
Lemma 9.5
(boundedness) For any \(0<t<1\) there exists a constant \(C(t)>0\) such that any \({\widehat{\Phi }}, \widehat{\varvec{\chi }} \in \textbf{V} + {\varvec{P}}_2({\mathcal {T}})\), \({\widehat{\Xi }} \in \textbf{V}+\textbf{M}({\mathcal {T}})\), and \(\Xi \in \textbf{V}\) satisfy
Proof of (a)
The definition of \(\gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\), Hölder inequalities, and \(\Vert \bullet \Vert _{L^{\infty }(\Omega )} \lesssim |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \(V+\text {M}({\mathcal {T}})\) from [8, Lemma 4.7] establish, for \({\widehat{\phi }}\), \({\widehat{\chi }} \in V + P_2({\mathcal {T}})\), \({\widehat{\xi }} \in V+\text {M}({\mathcal {T}})\), that
Proof of (b)
For \({\widehat{\phi }}\), \({\widehat{\chi }} \in V + P_2({\mathcal {T}})\) and \(\xi \in V\), the definition of \(\gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\), Hölder inequalities, and the continuous Sobolev embedding \(H^{1+t}(\Omega )\hookrightarrow L^\infty (\Omega )\) [4, Corollary 9.15] for \(t>0\) show
This and (9.4) conclude the proof. \(\square \)
Lemma 9.6
(approximation) Any \(\widehat{\varvec{\chi }} \in \textbf{V} + {\varvec{P}}_2({\mathcal {T}})\), \({\Phi },\textbf{v}\in \textbf{V}\), and \((\textbf{v}_2, \textbf{v}_{\textrm{M}}) \in {\varvec{P}}_2({\mathcal {T}})\times \textbf{M}({\mathcal {T}})\) satisfy
-
(a)
\(\Gamma _{\textrm{pw}}(\Phi ,\widehat{\varvec{\chi }}, (1 - {\varvec{J}}{\varvec{I}}_{\textrm{M}}) \textbf{v}_2) \lesssim h_{\textrm{max}} |\!|\!|\Phi |\!|\!||\!|\!|\widehat{\varvec{\chi }}|\!|\!|_{\textrm{pw}} \Vert \textbf{v} -\textbf{v}_2\Vert _{h}\),
-
(b)
\(\Gamma _{\textrm{pw}}((1 - {\varvec{J}}) \textbf{v}_{\textrm{M}}, \textbf{v}_2, \Phi ) \lesssim h_{\textrm{max}} |\!|\!|\textbf{v} - \textbf{v}_{\textrm{M}} |\!|\!|_{\textrm{pw}} |\!|\!|\textbf{v}_2|\!|\!|_{\textrm{pw}}|\!|\!|\Phi |\!|\!|.\)
Proof of (a)
For \(\phi \in V \), \({\widehat{\chi }} \in V + P_2({\mathcal {T}})\) and \( v_2 \in P_2({\mathcal {T}})\), the definition of \(\gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\), Hölder inequalities, and an inverse estimate \(h_T\Vert (1 - JI_{\textrm{M}}) v_2 \Vert _{L^{\infty }(T)}\lesssim \Vert (1 - JI_{\textrm{M}}) v_2 \Vert _{L^{2}(T)}\) lead to
This, Lemma 7.4.f, and the definition of \(\Gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) conclude the proof of (a).
Proof of (b)
For \(\phi \in V\), \( v_2 \in P_2({\mathcal {T}})\), and \(v_{\textrm{M}} \in \text {M}({\mathcal {T}})\), an introduction of \(\Pi _0\phi \) and \( \gamma _{\textrm{pw}}((1 - J)v_{\textrm{M}},v_2,\Pi _0 \phi )=0\) from Lemma 7.3.c and Remark 7.5 provide
Hölder inequalities and the estimate \(\Vert \phi - \Pi _0 \phi \Vert _{L^{\infty }(\Omega )} \lesssim h_{\textrm{max}}|\!|\!|\phi |\!|\!|\) [15, Theorem 3.1.5] provide
with \(|\!|\!|(1 - J)v_{\textrm{M}} |\!|\!|_{\textrm{pw}} \lesssim |\!|\!|v - v_{\textrm{M}} |\!|\!|_{\textrm{pw}}\) from Lemma 7.4.e in the last step. Recall (9.4) and (9.6) to conclude the proof of (b). \(\square \)
9.5 Proof of Theorem 9.1
The conditions in Theorem 5.1 are verified to establish the energy norm estimates. The hypotheses (2.3)–(2.6) follow from Lemma 7.7 (component-wise). The paper [11] has verified hypothesis (H1) for Morley/dG/\(C^0\)IP in the norm \(\Vert \bullet \Vert _h\) that is equivalent to \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}}\), \(\Vert \bullet \Vert _{\textrm{dG}}\), and \(\Vert \bullet \Vert _{\textrm{IP}}\) by Lemma 7.1.
For any \(\varvec{\theta }_{h} \in {{\textbf {V}}}_h\) with \(\Vert \varvec{\theta }_{h}\Vert _{{{\textbf {V}}}_h} = 1\), Lemma 9.5.b with \(|\!|\!|\bullet |\!|\!|_{\textrm{pw}} \le \Vert \bullet \Vert _{h}\) implies \({\widehat{b}}(R\varvec{\theta }_{h},\bullet ) \in \textbf{H}^{-1-t}(\Omega )\) for \(R \in \{{{{\textbf {i}}}}{{{\textbf {d}}}}, {\varvec{I}}_\text {M}, {{\varvec{J}}}{{\varvec{I}}}_\text {M}\}\). Therefore, there exists a unique \(\varvec{\chi } \in {{\textbf {V}}}\cap \textbf{H}^{3-t}(\Omega )\) with \(\Vert \varvec{\chi } \Vert _{\textbf{H}^{3-t}(\Omega )} \lesssim 1\) such that \(A(\varvec{\chi } ,\Phi ) = {\widehat{b}}(R\varvec{\theta }_h ,\Phi )\) for all \(\Phi \in {{\textbf {V}}}\). Hence, for Morley/dG schemes (resp. \(C^0\)IP scheme), the boundedness of R (from Lemma 7.7), Lemma 7.1 (resp. Remark 7.9), and Lemma 7.3.d provide (H2) with \(\delta _{2} \lesssim h_{\textrm{max}}^{1-t}\).
The proof of (H3) starts as in Sect. 8.5 and adopts Lemma 9.6.a (in place of Lemma 8.9.a) to establish (8.11) with \(t=0\) and the slightly sharper version \(\delta _3 \lesssim h_{\textrm{max}}\).
Since \(\delta _3=0\) for \(S=Q={{\varvec{J}}}{{\varvec{I}}}_\text {M}\), it remains \(S={{{\textbf {i}}}}{{{\textbf {d}}}}\) and \(={\varvec{I}}_{\textrm{M}}\) in the sequel to establish (H3). Given \({\varvec{y}}_{h}\) and \(\varvec{\theta }_{h} \in {{\textbf {V}}}_h\) of norm one, define \(\textbf{v}_2{{:}{=}}S{\varvec{y}}_{h} \in {\varvec{P}}_2({\mathcal {T}})\) and observe \(Q{\varvec{y}}_h ={{\varvec{J}}}{{\varvec{I}}}_\text {M}{\varvec{y}}_h={{\varvec{J}}}{{\varvec{I}}}_\text {M}\textbf{v}_2\) (by \(S={{{\textbf {i}}}}{{{\textbf {d}}}},{\varvec{I}}_{\textrm{M}})\). Hence with the definition of \({\widehat{b}}(\bullet ,\bullet )\), Lemma 9.6.a shows
The boundedness of R and \({\varvec{I}}_{\textrm{M}}\) and the equivalence of norms show \(|\!|\!|R\varvec{\theta }_h|\!|\!|_{\textrm{pw}}\Vert \textbf{v}_2\Vert _h \lesssim 1\) and hence \(\delta _{3} \lesssim h_{\textrm{max}}\).
As in the application for Navier-Stokes equations, Remark 7.9 leads to hypothesis (H4) with \(\delta _4 < \epsilon \). The existence and uniqueness of a discrete solution \(\Psi _h\) then follows from Theorem 4.1.
Note that for \(\textbf{v}_h \in \textbf{M}({\mathcal {T}})\), \(Q \textbf{v}_h={{\varvec{J}}}{{\varvec{I}}}_\text {M}\textbf{v}_h\). For Morley/dG/\(C^0\)IP, Lemma 9.6.a with \(\textbf{v}=0\) for \(S={{{\textbf {i}}}}{{{\textbf {d}}}}\); and Lemma 9.6.a with \(\textbf{v}_2\in \textbf{M}({\mathcal {T}})\) and \(\textbf{v}=0\) for \( S={\varvec{I}}_\text {M}\) show
The energy norm error control then follows from Theorem 5.1. \(\square \)
9.6 Proof of Theorem 9.3
Given \(2-\sigma \le s \le 2\) and \(G \in \textbf{H}^{-s}(\Omega )\) with \(\Vert G\Vert _{\textbf{H}^{-s}(\Omega )}=1\) , the solution \(z \in {{\textbf {V}}}\) to the dual problem (6.1) belongs to \( {{\textbf {V}}}\cap \textbf{H}^{4-s}(\Omega )\) by elliptic regularity. This and Lemma 7.3.d verify
Proof of Theorem 9.3.a
for \(R= {\varvec{J}} {\varvec{I}}_\text {M}\). The assumptions in Theorem 6.2 with \(X_{s}{{:}{=}} \textbf{H}^s({\mathcal {T}})\) are verified to establish the lower-order estimates. Hypothesis (\(\widehat{{\textbf {H1}}}\)) for Morley/dG/\(C^0\)IP schemes is verified in [11, Lemma 6.6] for an equivalent norm (with Lemma 7.1) and Lemma 7.7 for \(R = JI_{\textrm{M}}\) (applied component-wise to vector functions). The conditions (2.3)–(2.6) follow from Lemma 7.7. In Theorem 6.2, set \(z_h = {\varvec{I}}_h {\varvec{I}}_{\textrm{M}}z\) with \({\varvec{I}}_{h} = {{{\textbf {i}}}}{{{\textbf {d}}}}\) for Morley/dG resp. \({\varvec{I}}_h = {\varvec{I}}_{\textrm{C}}\) for \(C^0\)IP. Notice that (9.7) implies
for Morley/dG with \(\Vert \bullet \Vert _{\textrm{dG}} \approx |\!|\!|\bullet |\!|\!|_{\textrm{pw}}\) in \({{\textbf {V}}}+{{\textbf {M}}}({\mathcal {T}})\). Remark 7.9 and (9.7) provide (9.8) for \(C^0\)IP. For Morley/dG/\(C^0\)IP, Lemma 7.4.f implies \(\Vert \Psi _h- P\Psi _h \Vert _{\textbf{H}^{s}({\mathcal {T}})} \lesssim h_{\textrm{max}}^{2-{s}} \Vert \Psi - \Psi _h\Vert _{h}. \)
The difference \( {\Gamma }_{\textrm{pw}}(R \Psi _h,R \Psi _h,Qz_h) - \Gamma (P \Psi _h,P\Psi _h, Qz_h)\) vanishes for \(R={{\varvec{J}}}{{\varvec{I}}}_{\textrm{M}}=P\) (for all schemes). It remains to control the term \( {{\widehat{\Gamma }}}(\Psi ,\Psi ,(S-Q)z_h)\) for \(S \in \{ {{{\textbf {i}}}}{{{\textbf {d}}}}, {\varvec{I}}_{\textrm{M}}, {{\varvec{J}}}{{\varvec{I}}}_{\textrm{M}} \}\).
For \(S=Q={{\varvec{J}}}{{\varvec{I}}}_{\textrm{M}}\), \(\Gamma _{\textrm{pw}}(\Psi ,\Psi ,(S-Q)z_h )=0\). For \(S ={{{\textbf {i}}}}{{{\textbf {d}}}}\), Lemma 9.6.a and (9.8) establish
For \(S = {\varvec{I}}_{\textrm{M}}\), Lemma 9.6.a applies to \(\textbf{v}_h={\varvec{I}}_{\textrm{M}}z_h\). A triangle inequality and Lemma 7.7 reveal \(\Vert z-{\varvec{I}}_{\textrm{M}}z_h\Vert _h \lesssim \Vert z- z_h \Vert _h\lesssim h_{\textrm{max}}^{2-s}\) with (9.8) in the last step. Hence,
\(\square \)
Proof of Theorem 9.3.a
for \(R= {\varvec{I}}_\text {M}\). Elementary algebra and the symmetry of \(\Gamma _{\textrm{pw}}(\bullet ,\bullet ,\bullet )\) with respect to the first and second argument recast the last two terms on the right-hand side of Theorem 6.2 as
The arguments in (8.24)–(8.26) for \((\Psi ,\Psi _h)\) replacing \((u,u_h)\) and (9.8) reveal
This and Lemma 9.6.b for the first term in (9.9) (resp. Lemma 9.5.a and 7.4 .e for the second) show
This leads in (9.9) to
The remaining terms are controlled as in the above case \(R= {\varvec{J}}{\varvec{I}}_\text {M}\). This concludes the proof. \(\square \)
Proof of Theorem 9.3.b
Since \( \Psi _{h} = {\varvec{I}}_\text {M}\Psi _{\textrm{M}}\), and \(P=Q={\varvec{J}}\) for the Morley FEM, the last two terms of Theorem 6.2 read \({\Gamma }_{\textrm{pw}}( \Psi _{\textrm{M}},\Psi _{\textrm{M}},{\varvec{J}} {\varvec{I}}_\text {M}z_h) -{\Gamma }( {\varvec{J}}\Psi _{\textrm{M}}, {\varvec{J}}\Psi _{\textrm{M}},{\varvec{J}}{\varvec{I}}_\text {M}z_h)\) and are controlled in (9.10). This, Theorem 6.2, and the above estimates from the proof for \(R={\varvec{J}}{\varvec{I}}_\text {M}\) in (a) conclude the proof. \(\square \)
Proof of Theorem 9.4
The proofs at the abstract level in Sects. 2–6 follow as further explained for the Navier Stokes equations. A straightforward adoption of the arguments provided in the proofs of Theorem 9.1 and 9.3.a lead to (H2)-(H4) and the a priori error control. \(\square \)
References
Brenner, S.C., Gudi, T., Sung, L.Y.: A weakly over-penalized symmetric interior penalty method for the biharmonic problem. Electron. Trans. Numer. Anal. 37, 214–238 (2010)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 3rd edn. Springer, Berlin (2007)
Brenner, S.C., Sung, L.Y.: \(C^0\) interior penalty methods for fourth order elliptic boundary value problems on polygonal domains. J. Sci. Comput. 22(23), 83–118 (2005)
Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext, Springer, New York (2011)
Brezzi, F.: Finite element approximations of the von Kármán equations. RAIRO Anal. Numér. 12(4), 303–312 (1978)
Brezzi, F., Rappaz, J., Raviart, P.A.: Finite-dimensional approximation of nonlinear problems. I. Branches of nonsingular solutions. Numer. Math. 36(1), 1–25 (1980)
Carstensen, C., Gallistl, D., Nataraj, N.: Comparison results of nonstandard \(P_2\) finite element methods for the biharmonic problem. ESAIM Math. Model. Numer. Anal. 49, 977–990 (2015)
Carstensen, C., Mallik, G., Nataraj, N.: Nonconforming finite element discretization for semilinear problems with trilinear nonlinearity. IMA J. Numer. Anal. 41, 164–205 (2021)
Carstensen, C., Nataraj, N.: Adaptive Morley FEM for the von Kármán equations with optimal convergence rates. SIAM J. Numer. Anal. 59, 696–719 (2021)
Carstensen, C., Nataraj, N.: A priori and a posteriori error analysis of the Crouzeix–Raviart and Morley FEM with original and modified right-hand sides. Comput. Methods in Appl. Math. 21, 289–315 (2021)
Carstensen, C., Nataraj, N.: Lowest-order equivalent nonstandard finite element methods for biharmonic plates. ESAIM Math. Model. Numer. Anal. 56(1), 41–78 (2022)
Carstensen, C., Puttkammer, S.: How to prove the discrete reliability for nonconforming finite element methods. J. Comput. Math. 38(1), 142–175 (2020)
Cayco, M.E., Nicolaides, R.A.: Finite element technique for optimal pressure recovery from stream function formulation of viscous flows. Math. Comp. 46(174), 371–377 (1986)
Cayco, M.E., Nicolaides, R.A.: Analysis of nonconforming stream function and pressure finite element spaces for the Navier-Stokes equations. Comput. Math. Appl. 18(8), 745–760 (1989)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978)
Ciarlet, P.G.: Mathematical Elasticity: Theory of Plates, vol. II. North-Holland, Amsterdam (1997)
Ern, A., Guermond, J.L.: Finite Elements I: Approximation and Interpolation. Springer, New York (2021)
Feng, X., Karakashian, O.A.: Fully discrete dynamic mesh discontinuous Galerkin methods for the Cahn-Hilliard equation of phase transition. Math. Comp. 76(259), 1093–1117 (2007)
Gallistl, D.: Morley finite element method for the eigenvalues of the biharmonic operator. IMA J. Numer. Anal. 35(4), 1779–1811 (2015)
Grisvard, P.: Singularities in boundary value problems, vol. RMA 22, Masson & Springer-Verlag, (1992)
Kelley, C.T.: Iterative Methods for Linear and Nonlinear Equations, Frontiers in Applied Mathematics, vol. 16. Society for Industrial and Applied Mathematics, Philadelphia, PA (1995)
Mallik, G., Nataraj, N.: Conforming finite element methods for the von Kármán equations. Adv. Comput. Math. 42(5), 1031–1054 (2016)
Mallik, G., Nataraj, N.: A nonconforming finite element approximation for the von Kármán equations. ESAIM Math. Model. Numer. Anal. 50(2), 433–454 (2016)
Payne, L.E., Weinberger, H.F.: An optimal Poincaré inequality for convex domains. Arch. Rational Mech. Anal. 5(1960), 286–292 (1960)
Veeser, A., Zanotti, P.: Quasi-optimal nonconforming methods for symmetric elliptic problems. I— Abstract theory. SIAM J. Numer. Anal. 56(3), 1621–1642 (2018)
Veeser, A., Zanotti, P.: Quasi-optimal nonconforming methods for symmetric elliptic problems. III— Discontinuous Galerkin and other interior penalty methods. SIAM J. Numer. Anal. 56(5), 2871–2894 (2018)
Veeser, A., Zanotti, P.: Quasi-optimal nonconforming methods for symmetric elliptic problems. II— Overconsistency and classical nonconforming elements. SIAM J. Numer. Anal. 57(1), 266–292 (2019)
Zeidler, E.: Nonlinear Functional Analysis and its Applications. I, Fixed-Point Theorems. Springer-Verlag, New York (1986)
Acknowledgements
This paper is supported by the SPARC project (id 235) mathematics and computation of plates and the SERB POWER Fellowship SPF/2020/000019. The second author acknowledges the support by the IFCAM project “Analysis, Control and Homogenization of Complex Systems”.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carstensen, C., Nataraj, N., Remesan, G.C. et al. Unified a priori analysis of four second-order FEM for fourth-order quadratic semilinear problems. Numer. Math. 154, 323–368 (2023). https://doi.org/10.1007/s00211-023-01356-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-023-01356-w



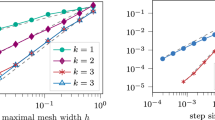

 for any
for any