Consistency results on Newmark methods for dynamical contact problems

Abstract

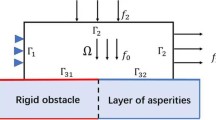
The paper considers the time integration of frictionless dynamical contact problems between viscoelastic bodies in the frame of the Signorini condition. Among the numerical integrators, interest focuses on the classical Newmark method, the improved energy dissipative version due to Kane et al., and the contact-stabilized Newmark method recently suggested by Deuflhard et al. In the absence of contact, any such variant is equivalent to the Störmer–Verlet scheme, which is well-known to have consistency order 2. In the presence of contact, however, the classical approach to discretization errors would not show consistency at all because of the discontinuity at the contact. Surprisingly, the question of consistency in the constrained situation has not been solved yet. The present paper fills this gap by means of a novel proof technique using specific norms based on earlier perturbation results due to the authors. The corresponding estimation of the local discretization error requires the bounded total variation of the solution. The results have consequences for the construction of an adaptive timestep control, which will be worked out subsequently in a forthcoming paper.