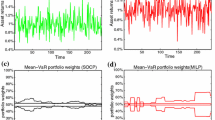
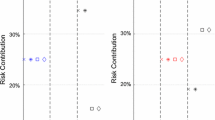
Abstract
Value-at-Risk, despite being adopted as the standard risk measure in finance, suffers severe objections from a practical point of view, due to a lack of convexity, and since it does not reward diversification (which is an essential feature in portfolio optimization). Furthermore, it is also known as having poor behavior in risk estimation (which has been justified to impose the use of parametric models, but which induces then model errors). The aim of this paper is to chose in favor or against the use of VaR but to add some more information to this discussion, especially from the estimation point of view. Here we propose a simple method not only to estimate the optimal allocation based on a Value-at-Risk minimization constraint, but also to derive—empirical—confidence intervals based on the fact that the underlying distribution is unknown, and can be estimated based on past observations.
Similar content being viewed by others
References
Acerbi C, Tasche D (2002) On the coherence of expected shortfall. J Bank Financ 26: 1487–1503
Alexander G, Baptista A (2002) Economic implications of using a mean-VaR model for portfolio selection: a comparison with mean-variance analysis. J Econ Dyn Control 26: 1159–1193
Artzner P, Delbaen F, Eber JM, Heath D (1999) Coherent measures of risk. Math Finance 9: 203–228
Basak S, Shapiro A (2001) Value-at-risk management: optimzl policies and asset prices. Rev Financ Stud 14: 371–405
Bawa VS (1978) Safety-first, stochastic dominance, and optimal portfolio choice. J Financ Quant Anal 13: 255–271
Beirlant J, Goegebeur Y, Segers J, Teugel J (2006) Statistics of extremes. Wiley/Interscience, New York
Charpentier A, Oulidi A (2007) Nonparametric quantile estimation. (submitted)
Cohen JB, Zinbarg ED (1967) Investment analysis and portfolio management. Homewood, Ill.: Richard D. Irwin, Inc.
Coles JL, Loewenstein U (1988) Equilibrium pricing and portfolio composition in the presence of uncertain parameters. J Financ Econ 22: 279–303
Cornish EA, Fisher RA (1937) Moments and cumulants in the specification of distributions. Rev Int Stat Inst 5: 307–320
Dowd K, Blake D (2006) After VaR : the theory, estimation, and insurance applications of quantile-based risk measures. J Risk Insur 73: 193–229
Duffie D, Pan J (1997) An overview of value at risk. J Deriv 4: 7–49
Embrechts P, Kluppelberg C, Mikosh T (1997) Modeling extremal events. Springer, Berlin
Feller GW (1968) Generalized asymptotic expansions of Cornish-Fisher type. Ann Math Stat 39: 1264–1273
Fishburn PC (1970) Utility theory for decision-making. Wiley, New York
Föllmer H, Schied A (2004) Stochastic finance: an introduction in discrete time. Walter de Gruyter, New York
Gaivoronski AA, Pflug G (2000) Value-at-Risk in portfolio optimization: properties and computational approach. Working Paper, 00-2, Norwegian University of Sciences & Technology
Gustafsson J, Hagmann J, Nielsen JP, Scaillet O (2006) Local Transformation Kernel Density Estimation of Loss. Cahier de Recherche 2006-10, HEC Genve
Harrel FE, Davis CE (1982) A new distribution free quantile estimator. Biometrika 69: 635–670
Hill GW, Davis AW (1968) Generalized asymptotic expansions of Cornish-Fisher type. Ann Math Stat 39: 1264–1273
Hyndman RJ, Fan Y (1996) Sample quantiles in statistical packages. Am Stat 50: 361–365
Ingersoll Jonathan E (1987) Theory of financial decision making. Rowman & Littlefield, 496 pp. ISBN:0847673596–9780847673599
Jorion P (1997) Value at risk : the new benchmark for controlling market risk. McGraw-Hill, New York
Kast R, Luciano E, Peccati L (1998) VaR and optimization: 2nd international workshop on preferences and decisions. Proceedings of the conference, Trento, 1–3 July 1998
Klein RW, Bawa VS (1976) The effect of estimation risk on optimal portfolio choice. J Financ Econ 3: 215–231
Kroll Y, Levy H, Markowitz HM (1984) Mean-variance versus direct utility maximization. J Financ 39: 47–61
Levy H, Sarnat M (1972) Safety first–an expected utility principle. J Financ Quant Anal 7: 1829–1834
Lemus G (1999) Portfolio optimization with quantile-based risk measures. Ph.D. Thesis. MIT
Litterman R (1997) Hot spots and edges II. Risk 10: 38–42
Markowitz HM (1952) Portfolio selection. J Financ 7: 77–91
Merton RC (1992) Continuous time finance 2nd edn. Blackwell Publishers, Oxford
Padgett WJ (1986) A kernel-type estimator of a quantile function from right-censored data. J Am Stat Assoc 81: 215–222
Park C (2006) Smooth nonparametric estimation of a quantile function under right censoring using beta kernels. Technical Report (TR 2006-01-CP), Departement of Mathematical Sciences, Clemson University
Quiggin J (1993) Generalized expected utility theory: the rank-dependent expected utility model. Kluwer/Nijhoff, Dordrecht/The Hague
Rockafellar RT, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2: 21–41
Roy AD (1952) Safety first and the holding of assets. Econometrica 20: 431–449
Waart AW van der (1998) Asymptotic statistics. Cambridge University Press, London
von Neumann J, Morgenstern O (1947) Theory of games and economic behaviour. Princeton University Press, Princeton
Wang S (1996) Premium calculation by transforming the layer premium density. ASTIN Bull 26: 71–92
Wirch J, Hardy M (1999) A synthesis of risk measures for capital adequacy. Insur Math Econ 25: 337–348
Yaari M (1987) A dual theory of choice under risk. Econometrica 55: 95–115
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Charpentier, A., Oulidi, A. Estimating allocations for Value-at-Risk portfolio optimization. Math Meth Oper Res 69, 395–410 (2009). https://doi.org/10.1007/s00186-008-0244-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-008-0244-7