Abstract
Using a controlled laboratory experiment, we examine individuals’ bid timing decisions in complete information all-pay auctions and find that homogeneous bidders are more likely to enter the early bidding stage under a favor-early tie-breaking rule. Furthermore, revenue in an endogenous-entry treatment, in which both sequential and simultaneous all-pay auctions exist, is either lower than or equal to that in an exogenous-entry treatment with only simultaneous all-pay auctions. Additionally, in simultaneous all-pay auctions, individuals do not always employ a mixed strategy as predicted by the risk-neutral model. Instead, our data is better rationalized by a risk- and loss-aversion model.










Similar content being viewed by others
Notes
An example is http://www.taskcn.com/w-60017.html, retrieved on October 15, 2011.
There is extensive literature on lottery contests in which the winning probability is not deterministic but proportional to the number of bids (Tullock 1980). We refer the reader to Dechenaux, Kovenock and Sheremeta Dechenaux et al. (2015) for a summary of this literature and the references therein.
We relegate the analysis for n players to the appendix.
We would like to thank one of the anonymous referees for pointing this out.
Strictly speaking, it is \(x^{*}_{e}=v/c_{2}+\epsilon \), and when \(\epsilon \rightarrow 0\), \(x^{*}_{e} \rightarrow v/c_{2}\).
Both the lottery choices and the post-experiment survey are included in online appendices.
We would like to thank one of the anonymous referees for suggesting this explanation.
Following Gneezy and Smorodinsky (2006), we use \(\text{ bids }\,{\le }5\) as the cutoff for “near-zero” bids. Moreover, the results are qualitatively similar when different cutoffs are used.
We would like to thank one of the anonymous referees for pointing this out.
Because only 1% of simultaneous all-pay auctions in endogenous treatments have both bidders in the early stage, we focus on simultaneous all-pay auctions with two late bidders.
The pairwise comparisons from non-parametric tests are consistent with regression results (ETB vs. LTB: 92 vs. 94, \(p=0.513\); ETB vs. exogenous: 92 vs. 102, \(p=0.513\); LTB vs. exogenous: 94 vs. 102, \(p=0.827\), rank-sum tests).
The non-parametric tests present the same results (ETB vs. LTB: 96 vs. 115, \(p=0.05\); ETB vs. Exogenous: 96 vs. 110, \(p=0.05\); LTB vs. Exogenous: 115 vs. 110, \(p=0.513\), rank-sum tests).
We compute the utilization ratio at the session level where the expected total bids are approximated by the average revenue and the expected highest bid is the average highest bid.
For homogeneous bidders, all players randomize, while for heterogeneous bidders, only players 1 and 2 randomize and others always bid 0.
\(G_{2}(0)\) is bidder 2’s probability of bidding 0. \(G_{2}^{rn}(0)\) is her probability of bidding 0 with risk and loss neutrality.
References
Amann E, Leininger W (1996) Asymmetric all-pay auctions with incomplete information: the two-player case. Games Econ Behav 14:1–18
Anderson LR, Stafford SL (2003) An experimental analysis of rent seeking under varying competitive conditions. Public Choice 115(1–2):199–216
Bartling B, Fehr E, Marechal MA, Schunk D (2009) Egalitarianism and competitiveness. Am Econ Rev 99(2):93–98
Baye MR, Kovenock D, de Vries CG (1994) The solution to the tullock rent-seeking game when \(R>2\): mixed-strategy equilibria and mean dissipation rates. Public Choice 81:363–380
Baye MR, Kovenock D, de Vries CG (1996) The all-pay auction with complete information. Econ Theory 8:291–305
Bouckaert J, Degryse H, de Vries CG (1992) Veilingen waarbij iedereen betaalt en toch iets wint. Tijdschrift voor economie en management 37(4):375–393
Brandts J, Holt CA (1993) Adjustment patterns and equilibrium selection in experimental signaling games. Int J Game Theory 22(3):279–302
Cabrales A, Nagel R, Armenter R (2007) Equilibrium selection through incomplete information in coordination games: an experimental study. Exp Econ 10(3):221–234
Cason TN, Masters WA, Sheremeta RM (2010) Entry into winner-take-all and proportional-prize contests: an experimentalstudy. J Public Econ 94:604–611
Shuchi C, Hrtline JD, Sivan B (2012) Optimal crowdsourcing contests. In: Proceedings of the twenty-third annual ACM-SIAM symposium on discrete algorithms, pp 856–868
Chen R, Chen Y (2011) The potential of social identity for equilibrium selection. Am Econ Rev 101(6):2562–2589
Davis DD, Reilly RJ (1998) Do too many cooks spoil the stew? An experimental analysis of rent-seeking and the role of a strategic buyer. Public Choice 95:89–115
Dechenaux E, Kovenock D, Sheremeta RM (2015) A survey of experimental research on contests, all-pay auctions and tournaments. Exp Econ 18(4):609–669
Dohmen T, Falk A (2011) Performance pay and multidimensional sorting: productivity, preferences, and gender. Am Econ Rev 101(2):556–590
Eriksson T, Teyssier S, Villeval M-C (2009) Self-selection and the efficiency of tournaments. Econ Inquiry 47:530–548
Ernst C, Thöni C (2013) Bimodal bidding in experimental all-pay auctions. Games 4(4):608–623
Fibich G, Gavious A, Sela A (2006) All-pay auctions with risk-averse players. Int J Game Theory 34(4):583–599
Fischbacher U (2007) z-Tree: Zurich toolbox for ready-made economic experiment. Exp Econ 10(2):171–178
Giulietti M, Price CW, Waterson M (2005) Consumer choice and competition policy: a study of uk energy markets. Econ J 115(506):949–968
Gneezy U, Smorodinsky R (2006) All-pay auction: an experimental study. J Econ Behav Org 61:255–275
Goeree JK, Holt CA (2005) An experimental study of costly coordination. Games Econ Behav 51(2):349–364
Grosskopf B, Rentschler L, Sarin R (2010) Asymmetric information in contests: theory and experiments. Working paper
Hillman A, Riley J (1989) Politically contestable rents and transfers. Econ Politics 1:17–40
Jian L, Li Z, Liu TX (2017) Simultaneous versus sequential all-pay auctions: an experimental study. Exp Econ 20(3):648–669
Kimbrough EO, Sheremeta RM, Shields TW (2014) When parity promotes peace: resolving conflict between asymmetric agents. J Econ Behav Org 99:96–108
Kirkegaard R (2012) Favoritism in asymmetric contests: head starts and handicaps. Games Econ Behav 76(1):226–248
Klose B, Sheremeta RM (2012) Behavior in all-pay and winner-pay auctions with identity-dependent externalities. Working paper
Konrad KA, Leininger W (2007) The generalized stackelberg equilibrium of the all-pay auction with complete information. Rev Econ Des 11(2):165–174
Krishna V, Morgan J (1997) An analysis of the war of attrition and the all-pay auction. J Econ Theory 72(2):343–362
Laury SK, Holt CA (2008) Voluntary provision of public goods: experimental results with interior Nash equilibria. In: Handbook of experimental economics results, vol 1. Elsevier, New York, pp 792–801
Leininger W (1991) Patent competition, rent dissipation, and the persistence of monopoly: the role of research budgets. J Econ Theory 53:146–172
Li Z (2015) (A)symmetric mixed strategy nash equilibrium in all-pay auctions with discrete strategy space. Working Paper
List JA (2007) On the interpretation of giving in dictator games. J Polit Econ 115(3):482–493
Lugovskyy V, Puzzello D, Tucker S (2010) An experimental investigation of overdissipation in the all pay auction. Eur Econ Rev 54(8):974–997
Mermer A (2013) Contests with expectation-based loss-averse players. Working paper
Morgan J (2003) Sequential contests. Public Choice 116(1):1–18
Morgan J, Orzen H, Sefton M (2012) Endogenous entry in contests. Econ Theory 51(2):435–463
Muller W, Schotter A (2010) Workaholics and dropouts in organizations. J Eur Econ Assoc 8:717–743
Noussair C, Silver J (2006) Behavior in all-pay auctions under incomplete information. Games Econ Behav 55(1):189–206
Olszewski W, Siegel R (2016) Large contests. Econometrica 84(2):835–854
Parco JE, Rapoport A, Amaldoss W (2005) Two-stage contests with budget constraints: an experimental study. J Math Psychol 49(4):320–338
Plott C, Smith V (1978) An experimental examination of two exchange institutions. Rev Econ Stud 45:133–153
Potters J, de Vries CG, van Winden F (1998) An experimental examination of rational rent-seeking. Eur J Polit Econ 14:783–800
Rentschler L, Turocy TL (2016) Two-bidder all-pay auctions with interdependent valuations, including the highly competitive case. J Econ Theory 163:435–466
Schlesinger H, Von der Schulenburg J-MG (1991) Search costs, switching costs and product heterogeneity in an insurance market. J Risk Insur 58(1):109–119
Segev E, Sela A (2014) Multi-stage sequential all-pay auctions. Eur Econ Rev 70:371–382
Sheremeta R (2010) Experimental comparison of multi-stage and one-stage contests. Games Econ Behav 68:731–747
Siegel R (2009) All-pay contests. Econometrica 77(1):71–92
Siegel R (2014) Asymmetric all-pay auctions with interdependent valuations. J Econ Theory 153:684–702
Tanaka T, Camerer CF, Nguyen Q (2010) Risk and time preferences: experimental and household data from Vietnam. Am Econ Rev 100(1):557–571
Terwiesch C, Xu Y (2008) Innovation contests, open innovation, and multiagent problem solving. Manag Sci 54(9):1529–1543
Tullock G (1980) Efficient Rent Seeking. In: Toward a theory of the rent-seeking society. Texas A&M University Press Press, Texas, pp 97–112
Vandegrift D, Yavas A (2010) An experimental test of sabotage in tournaments. J Inst Theoret Econ 166:259–285
Walker M, Wooders J (2001) Minimax play at Wimbledon. Am Econ Rev 91:1521–1538
Waterson M (2003) The role of consumers in competition and competition policy. Int J Ind Org 21(2):129–150
Weber RJ (1985) Auctions and competitive bidding. In: Peyton Young H (ed) Fair allocation, American mathematical society proceedings of symposia in applied mathematics, vol 33. American Mathematical Society, Providence, pp 143–170
Wooders J (2010) Does experience teach? Professionals and minimax play in the lab. Econometrica 78:1143–1154
Yang J, Adamic LA, Ackerman MS (2008) Crowdsourcing and knowledge sharing: strategic user behavior on taskcn. In: Proceedings of the 9th ACM conference on electronic commerce. ACM, pp 246–255
Author information
Authors and Affiliations
Corresponding author
Additional information
I would like to thank Yan Chen, Lada Adamic, Liuling Gong, Audrey Hu, Erin Krupka, Zheng Li, Baoping Liu, Jeffrey Mackie-Mason, Yusufcan Masatlioglu, Scott Page, Kan Takeuchi, Neslihan Uler, and the seminar participants at the North American Regional Meetings of the ESA (Tucson, AZ, November 2010) and the 2011 International Meetings of the ESA (Chicago, IL, July 2011). I thanks Robert Ketcham for his excellent research assistance in conducting the lab experiments. I am grateful to two anonymous referees and the Associate Editor for helpful comments and suggestions, which significantly improved the paper. The financial support from the School of Information and the Rackham Graduate School, University of Michigan, Tsinghua University, the National Natural Science Foundation of China (NSFC) under Grant 71403140, is greatly appreciated.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
A Proofs
1.1 Equilibrium characterization for all-pay auctions with n players
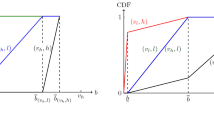
The analysis for heterogeneous bidders follows Konrad and Leininger (2007), and we focus on equilibrium characterization for homogeneous players. Assuming a favor-late tie-breaking rule, we first characterize the SPNE in sequential all-pay auctions.
Following Konrad and Leininger (2007), we first consider the subgame at the late stage (L). The maximum bids from the early stage (E) are characterized by \(\bar{x}_{E}\equiv \max _{i\in E} \{x_{i}\}\). \(x_{L}^{i}\) represents the best response in stage L for bidder i. Given \(\bar{x}_{E}\), we have:
-
1.
If \(c \bar{x}_{E}> v\), \(x_{L}^{i}=0\).
-
2.
If \(c \bar{x}_{E}= v\), if there is only one player in the late stage, she is indifferent between bidding v and 0. If there are more than one bidder, either all of them bid 0 or one of them bids v.
-
3.
If \(c \bar{x}_{E}<v\), if there is only one player in the late stage, she would bid \(\bar{x}_{E}\). If there are more than one bidder, it becomes a simultaneous all-pay auction with lower bound \(\bar{x}_{E}\), and the expected payoff for all late player is always 0.
Now we consider stage E. As \(\bar{x}_{L}\equiv \max _{i\in L} \{\bar{x}_{i}\}\) and \(\bar{x}_{i}=\bar{x}=\frac{v}{c}\) for homogeneous bidders, the equilibrium bids in stage E for bidder i: \(x_{E}^{i}\), is characterized below.
-
1.
If there is more than one bidder in stage E, there are two types of equilibrium strategies.
-
(a)
One player bids \(\bar{x}\) and all others bid 0.
-
(b)
All players bid 0.
-
(a)
-
2.
If there is one and only one bidder i in stage E, similarly, \(x_{E}^{i}=\{\bar{x},0\}\).
When all bidders enter either stage E or stage L together, the game becomes a simultaneous all-pay auction and the unique symmetric Nash equilibrium is that bidders randomize continuously on \([0,\bar{x}]\). The expected payoff for everyone is always 0.
Furthermore, when the bid timing decision is endogenous, conditional on the subgame where all early players bid 0 in the equilibrium, \(q^{*}_{i}=0\) is a best reply if \(\prod q_{j\ne i}>0\). Otherwise, \(q^{*}_{i} \in [0, 1]\). \(\square \)
Proof of Proposition 1
The proof for the unique symmetric NE follows the line of the argument in Baye et al. (1996), and we focus on the analysis of \(G_{1}(x)\) and \(G_{2} (x)\). The proof for homogeneous bidders is similar to \(G_{1}(x)\), so we omit it.
As the expected payoff for bidder 2 is always 0 in the equilibrium (Siegel 2009), we obtain:
Consequently,
The utility function is defined below:
As \(G_{1}(\frac{v}{2})u(\frac{v}{2})+(1-G_{1}(\frac{v}{2}))u(-\frac{v}{2})=0\), \( G_{1}(\frac{v}{2})=\frac{\lambda }{1+\lambda }\ge \frac{1}{2}\).
As \(\forall x \in (0, v)\), \(U_{2}(x)=0\) in the equilibrium, \(U'_{2}(x)=0\) and \(U''_{2}(x)=0\). Defining \(g_{1}(x)=G'_{1}(x)\), we obtain:
Furthermore, \(U_{2}''(x)=0\) yields the following equation:
Defining \(Z(x)=2g_{1}(x)(u'(v-x)-u'(-x))-G_{1}(x)u''(v-x)-(1-G_{1}(x))u''(-x)\), we show that \(Z(x)\le 0\) when \(0\le x \ll v\), and that \(Z(x)\ge 0\) when \(0\le v-x\ll v\).
First, \(\exists \) \(\frac{v}{2}\le x_{1}=\frac{v}{1+\lambda ^{\frac{1}{\alpha -1}}}<v\), \(u'(v-x_{1})=u'(-x_{1})\). As u(x) is concave with \(x\ge 0\), \(\forall \) \(x\ge x_{1}\), \(u'(v-x)\ge u'(-x)>0\), and by explicit calculation, \(u''(v-x)\le -u''(-x)<0\). Together with \(G_{1}(x)\ge \frac{1}{2}\), \(Z(x)\ge 0\).
Second, as \(G_{1}(\frac{v}{2})\ge \frac{1}{2}\), then \(\exists \) \(x_{0}\le \frac{v}{2}\), \(G(x_{0})=\frac{1}{2}\). Furthermore, \(\forall \) \(x \le x_{0}<x_{1}\), \(0<u'(v-x)\le u'(-x)\), and by explicit calculation, \(-u''(-x) \le u''(v-x)<0\). Together with \(G_{1}(x)\le \frac{1}{2}\), \(Z(x)\le 0\).
Because of the continuity of Z(x), \(\exists \) y where \(x_{0}\le y \le x_{1}\), \(Z(y)=0\) and \(g_{1}'(y)=0\). Now we show that y is unique.
If \(\exists \) \(Z(y_{1})=Z(y_{2})=0\), by the continuity of Z(x) and the intermediate value theorem, one of them, e.g., \(y_{1}\), must have \(Z'(y_{1})\le 0\). However, we know that
When \(x=y_{1}\), \(Z'(y_{1})=3g_{1}(y_{1})(u''(-y_{1})-u''(v-y_{1}))+G_{1}(y_{1})u'''(v-y_{1})+(1-G_{1}(y_{1}))u'''(-y_{1})>0\), which is a contradiction.
Along the same line of proof for \(G_{1}(x)\), \(G''_{2}(x)<0\) with \(0\le x \ll v\), and \(G''_{2}(x)>0\) with \(0\le v-x \ll v\). Additionally, as \(G_{2}(0)=\frac{u((1-c_{1})v)}{u(v)}\) and \(G^{rn}_{2}(0)=\frac{(1-c_{1})v}{v}\), by the concavity of u(x) with \(x\ge 0\), \(G_{2}(0)\ge G^{rn}_{2}(0) \). \(\square \)
B Experimental instruction
This is an experiment in decision-making. The experiment will proceed in two parts and you will make a series of decisions in each part. At the end, you will fill out a post-experiment questionnaire.
This experiment has 12 participants. Each of you has been randomly assigned an experiment ID at the beginning of the experiment. The experimenter will use this ID to pay you at the end of the experiment.
Rounds: The experiment consists of 30 rounds of two-person auctions.
Endowment: Each of you has 125 tokens as an endowment at the beginning of each round.
Prize Values: At the beginning of each round, an object with a value of 100 tokens will be auctioned within each two-person group.
Matching: At the beginning of each round, you will be randomly matched with another person. You are equally likely to be matched with any other person in the room.
Decisions: In each round, you must make two decisions. First, both you and your match choose independently and simultaneously which bidding stage you want to enter. The entry decisions are then announced to both of you. Second, you and your match each choose a bid in your respective bidding stage.
Bids: There are two bidding stages: the early stage and the late stage.
-
1.
If you enter early and your match enters late, you will choose a bid first. After observing your bid, your match will choose his or her bid.
-
2.
If you enter late and your match enters early, your match will choose a bid first. After observing his or her bid, you will choose your own bid.
-
3.
If both of you choose the same stage, you will bid simultaneously.
Cost of the Bid: The cost of the bid captures the idea that it is sometimes more or less costly to submit a bid. In the experiment, it is determined by a random number generator at the beginning of each round. For each round, with 50% chance, the cost of the bid is 1 token for you and 0.8 tokens for your match. With 50% chance, the cost of the bid is 0.8 tokens for you and 1 token for your match. Here is a numerical example:
-
1.
If the cost of your bid is 1 token and you bid 50, then you will pay 50 tokens.
-
2.
If the cost of your bid is 0.8 tokens and you bid 50, then you will pay 40 tokens.
Bid Range: Your bid can be any integer between 0 and 125, inclusive.
Profits: In each round, your profits will be determined by (1) your bid; (2) your match’s bid; (3) the cost of your bid; and (4) the entry decisions in the event of a tie.
Profits\(=\) Your Endowment- the cost of your bid*your bid + the value of the object if you win \(=\) 125—the cost of your bid*your bid+ 100 if you win
For example, in a given round, if you bid 40 and the cost of your bid is 0.8 in this round, then
-
1.
If you win the auction, then your profit is \(125-0.8*40+100 = 193\) tokens
-
2.
If you lose the auction, then your profit is \(125-0.8*40 = 93\) tokens
Note: You will always pay for your bid, which is equal to the cost of your bid* your bid, no matter whether you win or lose.
The tie-breaking rule: If you and your match bid exactly the same amount, and
-
1.
Both of you enter in the same stage, we will randomly choose one as the winner.
-
2.
If one and only one of you enter in the early stage, then the early bidder will be the winner.
Cumulative Profits: Your cumulative profits will be the sum of your profits in all rounds.
Feedback: At the end of each round, you will get the following feedback on your screen:
-
1.
Your entry decision
-
2.
Your match’s entry decision
-
3.
Your bid
-
4.
Your match’s bid
-
5.
Your profits
-
6.
Your match’s profits
-
7.
Your cumulative profits
History: In each round, your and your matches’ bids and entry decisions in each previous round, your and your matches’ profits in each previous round, as well as your cumulative profits up until the last round will be displayed in a history box.
Review Questions: To help you understand the experiment, we will go over nine review questions before we start the auction. You can also find these review questions in the appendix for your reference. You will get 25 tokens for answering each of the review questions correctly.
Exchange Rate: $1 = 250 tokens. Please do not communicate with each other during the experiment. If you have a question, feel free to raise your hand, and an experimenter will come to help you.
Rights and permissions
About this article
Cite this article
Liu, T.X. All-pay auctions with endogenous bid timing: an experimental study. Int J Game Theory 47, 247–271 (2018). https://doi.org/10.1007/s00182-017-0586-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-017-0586-6