Abstract
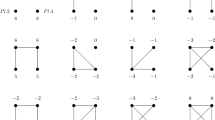
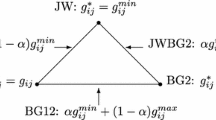
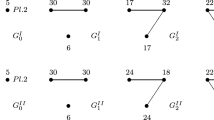
Suppose that individual payoffs depend on the network connecting them. Consider the following simultaneous move game of network formation: players announce independently the links they wish to form, and links are formed only under mutual consent. We provide necessary and sufficient conditions on the network link marginal payoffs such that the set of pairwise stable, pairwise-Nash and proper equilibrium networks coincide, where pairwise stable networks are robust to one-link deviations, while pairwise-Nash networks are robust to one-link creation but multi-link severance. Under these conditions, proper equilibria in pure strategies are fully characterized by one-link deviation checks.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Bala V, Goyal S (2000) A noncooperative model of network formation. Econometrica 68: 1181–1230
Bloch F, Jackson MO (2006) Definitions of equilibrium in network formation games. Int J Game Theory 34: 305–318
Bloch F, Jackson MO (2007) The formation of networks with transfers among players. J Econ Theory 133: 83–110
Calvó-Armengol A (2004) Job contact networks. J Econ Theory 115: 191–206
Dutta B, Tijs S, van den Nouweland A (1998) Link formation in cooperative situations. Int J Game Theory 27: 245–256
Dutta B, Mutuswami S (1997) Stable networks. J Econ Theory 76: 322–344
Fréchet M (1951) Sur les tableaux de corrélation dont les marges sont données. Ann l’Université Lyon 14: 53–77
Gilles R, Sarangi S (2005) Stable Networks and Convex Payoffs, Departmental Working Papers 2005-13, Department of Economics, Louisiana State University
Goyal S, Joshi S (2006) Unequal Connections. Int J Game Theory 34: 319–349
Jackson MO (2004) A survey of models of network formation: stability and efficiency, 2004. In: Demange G, Wooders M (eds) Group Formation in Economics; Networks, Clubs and Coalitions, Chapter 1. Cambridge University Press, Cambridge
Jackson MO, Rogers B (2006) Search in the formation of large networks: How random are socially generated networks?. Am Econ Rev (2006, forthcoming)
Jackson MO, Wolinsky A (1996) A strategic model of social and economic networks. J Econ Theory 71: 44–74
Jackson MO, Watts A (2001) The existence of pairwise stable networks. Seoul J Econ 14: 299–321
Jackson MO, Watts A (2002) The evolution of social and economic networks. J Econ Theory 106: 265–295
Jackson MO, van den Nouweland A (2005) Strongly stable networks. Games Econ Behav 51(2): 420–444
Mailath GJ, Samuelson L, Swinkels JM (1997) How proper is sequential equilibrium? Games Econ Behav 18: 193–218
Myerson RB (1978) Refinements of the Nash equilibrium concept. Int J Game Theory 7: 73–80
Myerson RB (1991) Game theory: analysis of conflict. Harvard University Press, Cambridge
Selten R (1975) Rexamination of the perfection concept for equilibrium points in extensive games. Int J Game Theory 4: 25–55
van Damme E (1984) A relation between perfect equilibria in extensive form games and proper equilibria in normal form games. Int J Game Theory 13: 1–13
Yamamoto Y (1993) A path-following procedure to find a proper equilibrium of finite games. Int J Game Theory 22: 249–259
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Antoni Calvó-Armengol heart breakingly passed away on 3 November 2007. His memory will forever remain radiant and warm, like he always was.
We thank William Thomson, an associate editor and two anonymous referees for their suggestions that led to substantial improvements. We also thank Sjaak Hurkens, Bettina Klaus, Jordi Massó and Giovanni Neglia for helpful conversations. The first author gratefully acknowledges the financial support from the Spanish Ministry of Education and FEDER through grant SEJ2005-01481/ECON, the Fundación BBVA and the Barcelona Economics Program of XREA. The second author is grateful to the Netherlands Organization for Scientific Research (NWO) for its support under grant VIDI-452-06-013.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Calvó-Armengol, A., İlkılıç, R. Pairwise-stability and Nash equilibria in network formation. Int J Game Theory 38, 51–79 (2009). https://doi.org/10.1007/s00182-008-0140-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-008-0140-7