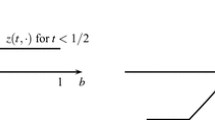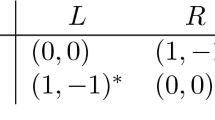Abstract
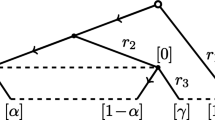
New characterizations of sequential equilibrium, perfect equilibrium, and proper equilibrium are provided that use nonstandard probability. It is shown that there exists a belief system μ such that \({(\vec{\sigma},\mu)}\) is a sequential equilibrium in an extensive game with perfect recall iff there exist an infinitesimal \({\epsilon}\) and a completely mixed behavioral strategy profile σ′ (so that \({\sigma_i'}\) assigns positive, although possibly infinitesimal, probability to all actions at every information set) that differs only infinitesimally from \({\vec{\sigma}}\) such that at each information set I for player i, σ i is an \({\epsilon}\)-best response to \({\vec{\sigma}'_{-i}}\) conditional on having reached I. Note that the characterization of sequential equilibrium does not involve belief systems. There is a similar characterization of perfect equilibrium; the only difference is that σ i must be a best response to \({\vec{\sigma}'_{-i}}\) conditional on having reached I. Yet another variant is used to characterize proper equilibrium.
Similar content being viewed by others
References
Basu S, Pollack R, Roy M-F (2003) Algorithms in real algebraic geometry. Algorithms and computation in mathematics, vol 10. Springer, Berlin
Blume L, Brandenburger A, Dekel E (1991) Lexicographic probabilities and equilibrium refinements. Econometrica 59(1): 81–98
Blume LE, Zame WR (1994) The algebraic geometry of perfect and sequential equilibrium. Econometrica 62: 783–794
Bochnak J, Coste M, Roy M-F (1998) Real algebraic geometry. Springer, Berlin
Enderton HB (1972) A mathematical introduction to logic. Academic Press, New York
Fishburn PC (1972) On the foundations of game theory: the case of non-Archimedean utilities. Int J Game Theory 1: 65–71
Halpern JY (2001) Lexicographic probability, conditional probability, and nonstandard probability. In: Theoretical aspects of rationality and knowledge: proceedings of eighth conference (TARK 2001). Morgan Kaufmann, San Francisco, pp 17–30. A full version of the paper can be found at http://arxiv.org/abs/cs/0306106
Hammond PJ (1994) Elementary non-Archimedean representations of probability for decision theory and games. In: Humphreys P (ed) Patrick Suppes: scientific philosopher, vol 1. Kluwer, Dordrecht, pp 25–49
Kreps DM (1990) Game theory and economic modeling. Oxford University Press, Oxford
Kreps DM, Wilson RB (1982) Sequential equilibria. Econometrica 50: 863–894
Myerson R (1978) Refinements of the Nash equilibrium concept. Int J Game Theory 7: 73–80
Osborne MJ, Rubinstein A (1994) A course in game theory. MIT Press, Cambridge
Rajan U (1998) Trembles in the Bayesian foundation of solution concepts. J Econ Theory 82: 248–266
Richter MK (1971) Rational choice. In: Chipman J, Hurwicz L, Richter MK, Sonnenschein HF(eds) Prefrence, utility, and demand. Harcourt, Brace, and Jovanovich, New York, pp 29–58
Robinson A (1973) Function theory on some nonarchimedean fields. Am Math Mon: Papers Found Math 80: S87–S109
Selten R (1975) Reexamination of the perfectness concept for equilibrium points in extensive games. Int J Game Theory 4: 25–55
Skala HJ (1974) Nonstandard utilities and the foundations of game theory. Int J Game Theory 3(2): 67–81
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported in part by NSF under grants CTC-0208535, ITR-0325453, and IIS-0534064, and by AFOSR under grant FA9550-05-1-0055.
An erratum to this article is available at http://dx.doi.org/10.1007/s00182-016-0537-7.
Rights and permissions
About this article
Cite this article
Halpern, J.Y. A nonstandard characterization of sequential equilibrium, perfect equilibrium, and proper equilibrium. Int J Game Theory 38, 37–49 (2009). https://doi.org/10.1007/s00182-008-0139-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-008-0139-0