Abstract
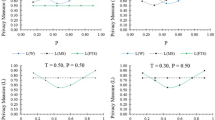
The present work proposes a new two-stage unrelated randomized response model to estimate the mean number of individuals who possess a rare sensitive attribute in a given population by using Poisson probability distribution, when the proportion of rare non-sensitive unrelated attribute is known and unknown. The properties of the proposed model are examined. The variance of the proposed randomized response model smaller than Land et al. (Stat J Theor Appl Stat, 46(3):351–360, 2012) and Singh and Tarray (Model Assist Stat Appl, 10(2):129–138, 2015) to estimate sensitive characteristic under study. The proposed model provides a more efficient unbiased estimator of the mean number of individuals. The procedure also introduces the measure of privacy protection of respondents and compares randomized response models in terms of efficiency and privacy protection. Empirical illustrations are presented to support the theoretical results and suitable recommendations are put forward to the survey statisticians/practitioners.




Similar content being viewed by others
Availability of data and material
Not applicable.
Code availability
Not applicable.
References
Anderson H (1977) Estimation of a proportion through randomized response. Int Stat Rev 44(2):213–217
Bhargava M, Singh R (2002) On the efficiency comparison of certain randomized response strategies. Metrika 55(3):191–197
Greenberg B, Abul-ela A-LA, Simmons WR, Horvitz DG (1969) The unrelated question randomized response model: Theoretical framework. J Am Stat Assoc 64(326):520–539
Kumar A, Singh GN, Vishwakarma GK (2019) An efficient survey technique for estimating the proportion and sensitivity attributes in a dichotomous finite population. Proc Natl Acad Sci India Sect A Phys Sci 90:281–287
Land M, Singh S, Sedory SA (2012) Estimation of a rare sensitive attribute using Poisson distribution. Stat J Theor Appl Stat 46(3):351–360
Lanke J (1976) On the degree of protection in randomized interviews. Int Stat Rev 44(2):197–203
Lee GS, Hong KH, Son CK (2016) A stratified two-stage unrelated randomized response model for estimating a rare sensitive attribute based on the Poisson distribution. J Stat Theory Pract 10(2):239–262
Lee GS, Uhm D, Kim JM (2013a) Estimation of a rare sensitive attribute in a stratified sample using Poisson distribution. Stat J Theor Appl Stat 47(3):575–589
Lee GS, Uhm D, Kim JM (2013b) Estimation of a rare sensitive attribute in probability proportional to size measure using Poisson distribution. Stat J Theor Appl Stat 48:685–709
Leysieffer FW, Warner SL (1976) Respondent jeopardy and optimal designs in randomized response models. J Am Stat Assoc 71(355):649–656
Narjis G, Shabbir J (2022) A two-stage unrelated question randomized response model for estimating the rare sensitive parameter under Poisson distribution. Commun Stat Theory Methods 51(6):1836–1856
Nayak TK (1994) On randomized response surveys for estimating a proportion. Commun Stat Theory Methods 23(11):3303–3321
Singh GN, Kumar A, Vishwakarma GK (2020) Estimation of population mean of sensitive quantitative character using blank cards in randomized device. Commun Stat Simul Comput 49(6):1603–1630
Singh HP, Tarray TA (2015) A revisit to the Singh, Horn, Singh and Mangat’s randomization device for estimating a rare sensitive attribute using Poisson distribution. Model Assist Stat Appl 10(2):129–138
Singh S, Horn S, Singh R, Mangat NS (2003) On the use of modified randomization device for estimating the prevalence of a sensitive attribute. Statin Transit 6(4):515–522
Solanki RS, Singh HP (2016) The improved estimation of ratio of two population proportions. Sociol Methods Res 45(1):158–174
Vishwakarma GK, Singh N (2021) Computing the effect of measurement errors under additive scramble response for sensitive variable. J Comput Appl Math 395:113593
Warner SL (1965) Randomized response: a survey technique for eliminating evasive answer bias. J Am Stat Assoc 60(309):63–69
Zhimin H, Zaizai Y (2012) Measure of privacy in randomized response model. Qual Quant 46(4):1167–1180
Acknowledgements
Authors are thankful to Editor Prof. Cathy W. S. Chen, the editorial board, and learned referees for their valuable comments which have made a substantial improvement to bring the original manuscript to its present form.
Funding
No funding was received to carry out this research work.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict and competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Vishwakarma, G.K., Kumar, A. & Kumar, N. Two-stage unrelated randomized response model to estimate the prevalence of a sensitive attribute. Comput Stat 39, 865–890 (2024). https://doi.org/10.1007/s00180-023-01326-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-023-01326-8
Keywords
- Poisson probability distribution
- Unrelated randomized response model
- Sensitive attribute
- Estimation of proportion
- Privacy protection