High-Quality Image Compressed Sensing and Reconstruction with Multi-scale Dilated Convolutional Neural Network | Circuits, Systems, and Signal Processing Skip to main content
Springer Nature Link
Log in

High-Quality Image Compressed Sensing and Reconstruction with Multi-scale Dilated Convolutional Neural Network

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

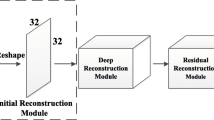
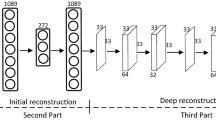
Deep learning (DL)-based compressed sensing (CS) has been applied for better performance of image reconstruction than traditional CS methods. However, most existing DL methods utilize the block-by-block measurement and each measurement block is restored separately, which introduces harmful blocking effects for reconstruction. Furthermore, the neuronal receptive fields of those methods are designed to be the same size in each layer, which can only collect single-scale spatial information and has a negative impact on the reconstruction process. This paper proposes a novel framework named multi-scale dilated convolution neural network for CS measurement and reconstruction. During the measurement period, we directly obtain all measurements from a trained measurement network, which employs fully convolutional structures and is jointly trained with the reconstruction network from the input image. It need not be cut into blocks, which effectively avoids the block effect. During the reconstruction period, we propose the multi-scale feature extraction (MFE) architecture to imitate the human visual system to capture multi-scale features from the same feature map, which enhances the image feature extraction ability of the framework and improves the performance of image reconstruction. In the MFE, there are multiple parallel convolution channels to obtain multi-scale feature information. Then, the multi-scale features information is fused and the original image is reconstructed with high quality. Our experimental results show that the proposed method performs favorably against the state-of-the-art methods in terms of PSNR and SSIM.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability Statement

The datasets analyzed during the current study are available in IEEE Transactions On Pattern Analysis And Machine Intelligence paper “Contour detection and hierarchical image segmentation” [3].

Abbreviations

M :

The length of the measurement vector

N :

The length of the original signal vector

MR:

The measurement rate defined as \({\text {MR}}=M/N\)

\(\varvec{x}\) :

An original signal vector with size of \(N{\times }1\)

\(\varvec{y}\) :

A \(M{\times }1\) measurement vector

\(\varvec{\Phi }\) :

A \(M{\times }N\) CS matrix

\(\varvec{\Psi }\) :

A \(N{\times }N\) sparse representation matrix

\(\varvec{s}\) :

A \(N{\times }1\) sparse transform coefficients vector

K :

The sparsity of \(\varvec{x}\)

\(\delta _K\) :

The RIP parameter

d :

The dilated factor

B :

The size of blocks of the input image

\(\varvec{X_i}\) :

The ith block vector of the original signal

\(\varvec{Y_i}\) :

The ith block vector of the measurement

\(\varvec{\Phi _B}\) :

The block measurement matrix

\(\varvec{X}\) :

The original input image matrix

\(\varvec{Y}\) :

The measurement matrix for image compression

\(\varvec{X_1}\) :

The initial reconstruction image matrix

\(\varvec{X_j}\) :

The jth input image matrix

\(\varvec{X^*}\) :

The reconstruction image matrix

\(\varvec{{\mathcal {M}}}\) :

A tensor of multi-scale feature maps

\(\varvec{w_1, w_2, w_s, w_l}\) :

The weight matrix of the convolutional layer

\(\varvec{b}\) :

The bias vector of the convolutional layer

\(\varvec{\Theta }\) :

The parameter set of the MsDCNN

References

  1. N. Ahn, B. Kang, K.A. Sohn, Fast, accurate, and lightweight super-resolution with cascading residual network, in European Conference on Computer Vision (2018), pp. 252–268

  2. F. Albu, Leading element dichotomous coordinate descent exponential recursive least squares algorithm for multichannel active noise control, in Proceedings of AAS Acoustics (2012), pp. 21–23

  3. P. Arbelaez, M. Maire, C.C. Fowlkes, Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 33(5), 898–916 (2011)

    Article  Google Scholar 

  4. L. Bo, H. Lu, Y. Lu, J. Meng, W. Wang, FompNet: compressive sensing reconstruction with deep learning over wireless fading channels, in International Conference on Wireless Communications and Signal Processing (2017), pp. 1–6

  5. E.J. Candes, J. Romberg, T. Tao, Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52(4), 489–509 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  6. M.A. Davenport, D. Needell, M.B. Wakin, Signal space CoSaMP for sparse recovery with redundant dictionaries. IEEE Trans. Inf. Theory 59(10), 6820–6829 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Z. Deng, L. Zhu, X. Hu, Deep multi-model fusion for single-image dehazing, in IEEE International Conference on Computer Vision (2019), pp. 2453–2462

  8. C. Dong, C.C. Loy, K. He, A deep convolutional network for image super-resolution, in European Conference on Computer Vision (2014), pp. 184–199

  9. X. Dong, L. Wang, X. Sun, X. Jia, L. Gao, Remote sensing image super-resolution using second-order multi-scale networks. IEEE Trans. Geosci. Remote Sens. 59(4), 1–13 (2020)

    Google Scholar 

  10. L. Fang, C. Wang, S. Li, H. Rabbani, X. Chen, Z. Liu, Attention to lesion: lesion-aware convolutional neural network for retinal optical coherence tomography image classification. IEEE Trans. Med. Imaging 38(8), 1959–1970 (2019)

    Article  Google Scholar 

  11. L. Gan, Block compressed sensing of natural images, in International Conference on Digital Signal Processing (2007), pp. 403–406

  12. X. Han, G. Zhao, X. Li et al., Sparse signal reconstruction via expanded subspace pursuit. J. Appl. Remote Sens. 13(4), 1–11 (2019)

    Article  Google Scholar 

  13. K. He, X. Zhang, S. Ren, Deep residual learning for image recognition, in IEEE International Conference on Computer Vision (2016), pp. 770–778

  14. L. Kang, J. Huang, J. Huang, Adaptive subspace OMP for infrared small target image, in IEEE International Conference on Signal Processing (2018), pp. 445–449

  15. T. Kattenborn, J. Leitloff, F. Schiefer et al., Review on convolutional neural networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 173, 24–49 (2021)

    Article  Google Scholar 

  16. S. Katoch, S.S. Chauhan, V. Kumar, A review on genetic algorithm: past, present, and future. Multimedia Tools Appl. 5, 8091–8126 (2021)

    Article  Google Scholar 

  17. K. Kulkarni, S. Lohat, P. Turaga, Reconnet: non-iterative reconstruction of images from compressively sensed measurements, in IEEE International Conference on Computer Vision (2016), pp. 449–458

  18. W. Lai, J. Huang, N. Ahuja, Fast and accurate image super-resolution with deep Laplacian pyramid networks. IEEE Trans. Pattern Anal. Mach. Intell. 41(11), 2599–2613 (2019)

    Article  Google Scholar 

  19. C. Li, X. Liu, K. Yu, X. Wang, F. Zhang, Debiasing of seismic reflectivity inversion using basis pursuit denoising algorithm. J. Appl. Geophys. 177, 1–11 (2020)

    Article  Google Scholar 

  20. C. Li, W. Yin, H. Jiang, Y. Zhang, An efficient augmented Lagrangian method with applications to total variation minimization. Comput. Optim. Appl. 56(3), 507–530 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. J. Li, F. Fang, K. Mei, Multi-scale residual network for image super-resolution, in European Conference on Computer Vision (2018), pp. 8–14

  22. W. Li, M. Niu, Y. Zhang, Y. Huang, Forward-looking scanning radar superresolution imaging based on second-order accelerated iterative shrinkage-thresholding algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 13, 620–631 (2020)

    Article  Google Scholar 

  23. Z. Li, C. Peng, G. Yu, X. Zhang, Y. Deng, J. Sun, Detnet: design backbone for object detection, in European Conference on Computer Vision (2018), pp. 334–350

  24. Q.S. Lian, L.P. Fu, S.Z. Chen, B.S. Shi, A Compressed sensing algorithm based on multi-scale residual reconstruction network. Acta Autom. Sin. 45(11), 2082–2091 (2019)

    Google Scholar 

  25. T. Lin, S. Ma, Y. Ye, S. Zhang, An ADMM-based interior-point method for large-scale linear programming. Optim. Methods Softw. 36, 1–36 (2020)

    MathSciNet  Google Scholar 

  26. J. Liu, X. Du, A gradient projection method for the sparse signal reconstruction in compressive sensing. Appl. Anal. 97, 2122–2131 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. A. Mousavi, A.B. Patel, R.G. Baraniuk, A deep learning approach to structured signal recovery, in IEEE 53rd Annual Allerton Conference on Communication, Control, and Computing (2015), pp. 1336–1343

  28. A. Mujahid, M.J. Awan, A. Yasin, M.A. Mohammed, R. Damaševičius, R. Maskeliūnas, K.H. Abdulkareem, Real-time hand gesture recognition based on deep learning YOLOv3 model. Appl. Sci. 11, 1–12 (2021)

    Article  Google Scholar 

  29. D. Needell, R. Vershynin, Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 9(3), 317–334 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. R. Prabhu, X. Yu, Z. Wang, U-Finger: multi-scale dilated convolutional network for fingerprint image denoising and inpainting, in Inpainting and Denoising Challenges (2019), pp. 45–50

  31. T. Saha, S. Srivastava, S. Khare, An improved algorithm for basis pursuit problem and its applications. Appl. Math. Comput. 355, 385–398 (2019)

    MathSciNet  MATH  Google Scholar 

  32. K. Schnass, Average performance of orthogonal matching pursuit (OMP) for sparse approximation. IEEE Signal Process. Lett. 25(12), 1865–1869 (2018)

    Article  Google Scholar 

  33. W. Shi, F. Jiang, S. Liu, D. Zhao, Image compressed sensing using convolutional neural network. IEEE Trans. Image Process. 29, 375–388 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. C. Stanciu, C. Anghel, C. Paleologu, J. Benesty, F. Albu, S. Ciochina, Leading element dichotomous coordinate descent exponential recursive least squares algorithm for multichannel active noise control, in IEEE ISSCS 2011 (2011), pp. 1–4

  35. T. Tirer, R. Giryes, Generalizing CoSaMP to signals from a union of low dimensional linear subspaces. Appl. Comput. Harmonic Anal. 49(1), 99–122 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. H. Yao, F. Dai, S. Zhang, DR2-Net: deep residual reconstruction network for image compressive sensing. Neurocomputing 35, 483–493 (2019)

    Article  Google Scholar 

  37. S. Yao, Q. Guan, S. Wang et al., Fast sparsity adaptive matching pursuit algorithm for large-scale image reconstruction. EURASIP J. Wirel. Commun. Netw. 2018(1), 1–8 (2018)

    Article  Google Scholar 

  38. Y.V. Zakharov, T.C. Tozer, Multiplication-free iterative algorithm for LS problem. Electron. Lett. 40(9), 567 (2004)

    Article  Google Scholar 

  39. A. Zarei, B.M. Asl, Automatic seizure detection using orthogonal matching pursuit, discrete wavelet transform, and entropy based features of eeg signals. Comput. Biol. Med. 131(5), 1–14 (2021)

    Google Scholar 

  40. C. Zeng, J. Ye, Z. Wang et al., Cascade neural network-based joint sampling and reconstruction for image compressed sensing. Signal Image Video Process. 16, 1–8 (2022)

    Article  Google Scholar 

  41. J. Zhang, B. Ghanem, ISTA-Net: interpretable optimization-inspired deep network for image compressive sensing, in IEEE International Conference on Computer Vision (2018), pp. 1828–1837

  42. K. Zhang, W. Zuo, Y. Chen, D. Meng, L. Zhang, Beyond a gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 26(7), 3142–3155 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  43. L. Zhang, Image adaptive reconstruction based on compressive sensing via CoSaMP, in International Conference on Information Science and Control Engineering (2013), pp. 760–763

  44. Y. Zhang, K. Li, Image super-resolution using very deep residual channel attention networks, in European Conference on Computer Vision (2018), pp. 286–301

Download references

Acknowledgements

The research work of this paper was supported by the National Natural Science Foundation of China (Nos. 62177022, 61901165, 61501199), Collaborative Innovation Center for Informatization and Balanced Development of K-12 Education by MOE and Hubei Province (No. xtzd2021-005), and Self-determined Research Funds of CCNU from the Colleges’ Basic Research and Operation of MOE (No. CCNU22QN013).

Author information

Authors and Affiliations

  1. Department of Digital Media Technology, Central China Normal University, Wuhan, 430079, China

    Zhifeng Wang

  2. Hubei Key Laboratory for High-efficiency Utilization of Solar Energy and Operation Control of Energy Storage System, Hubei University of Technology, Wuhan, 430068, China

    Zhenghui Wang, Chunyan Zeng, Yan Yu & Xiangkui Wan

Authors
  1. Zhifeng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhenghui Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chunyan Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yan Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiangkui Wan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chunyan Zeng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Z., Wang, Z., Zeng, C. et al. High-Quality Image Compressed Sensing and Reconstruction with Multi-scale Dilated Convolutional Neural Network. Circuits Syst Signal Process 42, 1593–1616 (2023). https://doi.org/10.1007/s00034-022-02181-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-022-02181-6

Keywords

Search

Navigation