Mixed Near-Field and Far-field Source Localization Using COLD Arrays | Circuits, Systems, and Signal Processing
Skip to main content
Springer Nature Link
Log in

Mixed Near-Field and Far-field Source Localization Using COLD Arrays

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

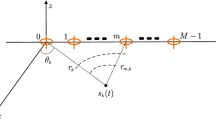
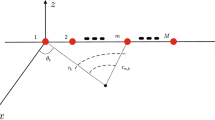
Many mixed near-field (NF) and far-field (FF) source localization algorithms in the open literature are developed based on the Fresnel approximation model, which is a simplified model of the exact source-array spatial geometry. Unlike these algorithms, in this paper, a new algorithm is derived to localize a mixture of NF and FF electromagnetic sources based on the exact spatial model with the use of a linear cocentered orthogonal loop and dipole (COLD) array. The summation of the dipole covariance matrix and the loop covariance matrix is shown to be independent of the source polarization parameters. Using this property, a multiple signal classification (MUSIC) pseudo-spectrum is defined for joint angle and range estimation. To facilitate the computational efficiency of the algorithm, a set of coarse angle and range estimates are derived using the estimating signal parameter via rotational invariance techniques (ESPRIT) philosophy to initiate the MUSIC searching. The major advantage of the proposed algorithm over the existing algorithms is that it does not introduce the systematic errors caused by the mismatch between the exact model and the Fresnel approximation model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

  1. H. Chen, W. Liu, W.-P. Zhu, M.N.S. Swamy, Q. Wang, Mixed rectilinear sources localization under unknown mutual coupling. J. Frankl. Inst. 356(4), 2372–2394 (2019)

    Article  MathSciNet  Google Scholar 

  2. J.P. Delmas, M.N.E. Korso, H. Gazzah, M. Castella, CRB analysis of planar antenna arrays for optimizing near-field source localization. Signal Process. 127, 117–134 (2016)

    Article  Google Scholar 

  3. B. Friedlander, Localization of signals in the near-field of an antenna array. IEEE Trans. Signal Process. 67(15), 3885–3893 (2019)

    Article  Google Scholar 

  4. J. He, M.N.S. Swamy, M.O. Ahmad, Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources. IEEE Trans. Signal Process. 60(4), 2066–2070 (2012)

    Article  MathSciNet  Google Scholar 

  5. J. He, L. Li, T. Shu, Near-field parameter estimation for polarized source using spatial amplitude ratio. IEEE Commun. Lett. 24(9), 1961–1965 (2020)

    Article  Google Scholar 

  6. J. He, L. Li, T. Shu, Localization of near-field sources for exact source-sensor spatial geometry. IEEE Signal Process. Lett. 27, 1040–1044 (2020)

    Article  Google Scholar 

  7. J. He, L. Li, T. Shu, T.-K. Truong, Mixed near-field and far-field source localization based on exact spatial propagation geometry. IEEE Trans. Veh. Technol. 70(4), 3540–3551 (2021)

    Article  Google Scholar 

  8. Y. Hsu, K.T. Wong, L. Yeh, Mismatch of near-field bearing range spatial geometry in source-localization by a uniform linear array. IEEE Trans. Antennas Propag. 59(10), 3658–3667 (2011)

    Article  Google Scholar 

  9. J. Jiang, F. Duan, J. Chen, Y. Li, X. Hua, Mixed near-field and far-field sources localization using the uniform linear sensor array. IEEE Sens. J. 13(8), 3136–3143 (2013)

    Article  Google Scholar 

  10. J. Jiang, F. Duan, X. Wang, An efficient classification method of mixed sources. IEEE Sens. J. 16(10), 3731–3734 (2016)

    Article  Google Scholar 

  11. D.H. Johnson, D.E. Dudgeon, Array Signal Processing: Concepts and Techniques (Prentice-Hall, Upper Saddle River, 1993)

    MATH  Google Scholar 

  12. H. Krim, M. Viberg, Two decades of array signal processing research: the parametric approach. IEEE Signal Process. Mag. 13(4), 67–94 (1996)

    Article  Google Scholar 

  13. J. Li, P. Stoica, D. Zheng, Efficient direction and polarization estimation with a COLD array. IEEE Trans. Antennas Propag. 44(4), 539–547 (1996)

    Article  Google Scholar 

  14. J. Liang, D. Liu, Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm. IEEE Trans. Signal Process. 58(1), 108–120 (2010)

    Article  MathSciNet  Google Scholar 

  15. G. Liu, X. Sun, Efficient method of passive localization for mixed far-field and near-field sources. IEEE Antennas Wirel. Propag. Lett. 12, 902–905 (2013)

    Article  Google Scholar 

  16. G. Liu, X. Sun, Two-stage matrix differencing algorithm for mixed far-field and near-field sources classification and localization. IEEE Sens. J. 14(6), 1957–1965 (2014)

    Article  Google Scholar 

  17. G. Liu, X. Sun, Spatial differencing method for mixed far-field and near-field sources localization. IEEE Signal Process. Lett. 21(11), 1331–1335 (2014)

    Article  Google Scholar 

  18. A.M. Molaei, B. Zakeri, S.M. Hosseini Andargoli, Components separation algorithm for localization and classification of mixed near-field and far-field sources in multipath propagation. IEEE Trans. Signal Process. 68, 404–419 (2020)

    Article  MathSciNet  Google Scholar 

  19. S. Pasupathy, W.J. Alford, Range and bearing estimation in passive sonar. IEEE Trans. Aerosp. Electron. Syst. 16(2), 244–249 (1980)

    Article  Google Scholar 

  20. R. Roy, T. Kailath, ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 37(7), 984–995 (1989)

    Article  Google Scholar 

  21. R.O. Schmidt, Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 34(3), 276–280 (1986)

    Article  Google Scholar 

  22. T. Shu, L. Li, J. He, Near-field localization for non-circular sources in the presence of sensor phase uncertainties. IEEE Wirel. Commun. Lett. 10(3), 562–566 (2021)

    Article  Google Scholar 

  23. T. Shu, J. He, L. Li, Near-field passive localization and gain-phase compensation with partly calibrated arrays. IEEE Trans. Aerosp. Electron. Syst. (2021). https://doi.org/10.1109/TAES.2021.3098111

    Article  Google Scholar 

  24. T. Shu, J. He, V. Dakulagi, 3-D near-field source localization using a spatially spread acoustic vector sensor. IEEE Trans. Aerosp. Electron. Syst. (2021). https://doi.org/10.1109/TAES.2021.3092703

    Article  Google Scholar 

  25. H.L. Van Trees, Optimum Array Processing, Part IV of Detection, Estimation, and Modulation Theory (Wiley, New York, 2002)

    Google Scholar 

  26. L. Wan, K. Liu, Y.-C. Liang, T. Zhu, DOA and polarization estimation for non-circular signals in 3-D millimeter wave polarized massive MIMO systems. IEEE Trans. Wirel. Commun. 20(5), 3152–3167 (2021)

    Article  Google Scholar 

  27. B. Wang, J. Liu, X. Sun, Mixed sources localization based on sparse signal reconstruction. IEEE Signal Process. Lett. 19(8), 487–490 (2012)

    Article  Google Scholar 

  28. B. Wang, Y. Zhao, J. Liu, Mixed-order MUSIC algorithm for localization of far-field and near-field sources. IEEE Signal Process. Lett. 20(4), 311–314 (2013)

    Article  Google Scholar 

  29. K. Wang, L. Wang, J. Shang, X. Qu, Mixed near-field and far-field source localization based on uniform linear array partition. IEEE Sens. J. 16(22), 8083–8090 (2016)

    Google Scholar 

  30. M. Wax, T. Kailath, Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Signal Process. 33(4), 387–392 (1985)

    Article  MathSciNet  Google Scholar 

  31. F. Wen, J. Shi, Z. Zhang, Closed-form estimation algorithm for EMVS-MIMO radar with arbitrary sensor geometry. Signal Process. 186, 108117 (2021)

    Article  Google Scholar 

  32. G. Zheng, Y. Song, C. Chen, Height measurement with meter wave polarimetric MIMO radar: signal model and MUSIC-like algorithm. Signal Process. (2022). https://doi.org/10.1016/j.sigpro.2021.108344

    Article  Google Scholar 

  33. Z. Zheng, M. Fu, D. Jiang, W. Wang, S. Zhang, Localization of mixed far-field and near-field sources via cumulant matrix reconstruction. IEEE Sens. J. 18(18), 7671–7680 (2018)

    Article  Google Scholar 

  34. Z. Zheng, J. Sun, W. Wang, H. Yang, Classification and localization of mixed near-field and far-field sources using mixed-order statistics. Signal Process. 143, 134–139 (2018)

    Article  Google Scholar 

  35. Z. Zheng, M. Fu, W. Wang, H.C. Ho, Mixed far-field and near-field source localization based on subarray cross-cumulant. Signal Process. 150, 51–56 (2018)

    Article  Google Scholar 

  36. Z. Zheng, M. Fu, W. Wang, S. Zhang, Y. Liao, Localization of mixed near-field and far-field sources using symmetric double-nested arrays. IEEE Trans. Antennas Propag. 67(11), 7059–7070 (2019)

    Article  Google Scholar 

  37. Z. Zheng, M. Fu, W. Wang, H.C. So, Symmetric displaced coprime array configurations for mixed near and far field source localization. IEEE Trans. Antennas Propag. 69(1), 465–477 (2021)

    Article  Google Scholar 

  38. W. Zuo, J. Xin, N. Zheng, A. Sano, Subspace-based localization of far-Field and near-field signals without eigendecomposition. IEEE Trans. Signal Process. 66(17), 4461–4476 (2018)

    Article  MathSciNet  Google Scholar 

  39. W. Zuo, J. Xin, W. Liu, N. Zheng, H. Ohmori, A. Sano, Localization of near-field sources based on linear prediction and oblique projection operator. IEEE Trans. Signal Process. 67(2), 415–430 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Key Laboratory of Adaptive Optics, Chinese Academy of Sciences, Chengdu, 610209, Sichuan, China

    Kejun Yin & Yun Dai

  2. School of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu, 610054, Sichuan, China

    Kejun Yin & Chunming Gao

  3. Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, 610209, Sichuan, China

    Kejun Yin & Yun Dai

Authors
  1. Kejun Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yun Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chunming Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kejun Yin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yin, K., Dai, Y. & Gao, C. Mixed Near-Field and Far-field Source Localization Using COLD Arrays. Circuits Syst Signal Process 41, 3642–3655 (2022). https://doi.org/10.1007/s00034-021-01945-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-021-01945-w

Keywords

Search

Navigation