Abstract
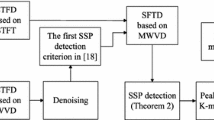
This paper proposes a novel underdetermined blind identification method with several new single-source points (SSPs) detection criteria for uniform linear array, where the mixing matrix is complex-valued. These new criteria are based on quadratic time–frequency distribution and employed to detect the SSPs so that the complex-valued mixing matrix can be estimated more precisely. To further enhance the estimation accuracy, a modified peak detection method is presented by exploiting the known source number. Finally, the complex-valued mixing matrix can be obtained by performing a clustering algorithm on samples at selected SSPs. One of the outstanding superiorities for the proposed algorithm is that the new criteria are strict enough for the points that are not the SSPs, which ensures the estimation accuracy of the mixing matrix. The other is that the performance of estimation precision is high even in the noisy case. Numerical simulation results verify the superiority of the proposed algorithm over the existing algorithms.









Similar content being viewed by others
References
F. Abrard, Y. Deville, A time–frequency blind signal separation method applicable to underdetermined mixtures of dependent sources. Signal Process. 8(2), 1389–1403 (2005)
G. Bao, Z. Ye, X. Xu et al., A compressed sensing approach to blind separation of speech mixture based on a two-layer sparsity model. IEEE Trans. Audio Speech Lang. Process. 21(5), 899–906 (2013)
P. Bofill, M. Zibulevsky, Underdetermined blind source separation using sparse representations. Signal Process. 81(11), 2353–2362 (2001)
Y. Cai, D. Liu, Multiuser detection using the Taguchi method for DS-CDMA systems. IEEE Trans. Wirel. Commun. 4(4), 1594–1607 (2005)
P. Comon, C. Jutten, Handbook of Blind Source Separation: Independent Component Analysis and Applications (Academic press, New York, 2010)
T. Dong, Y. Lei, J. Yang, An algorithm for underdetermined mixing matrix estimation. Neurocomputing 104, 26–34 (2013)
P. Georgiev, F. Theis, A. Cichocki, Sparse component analysis and blind source separation of underdetermined mixtures. IEEE Trans. Neural Netw. 16(4), 992–996 (2005)
M. Küdhne, R. Togneri, S. Nordholm, A new evidence model for missing data speech recognition with applications in reverberant multisource environments. IEEE Trans. Audio Speech Lang. Process. 19(2), 372–384 (2011)
L.D. Lathauwer, J. Castaing, Blind identification of underdetermined mixtures by simultaneous matrix diagonalization. IEEE Trans. Signal Process. 56(3), 1096–1105 (2008)
H. Li, Y. Shen, J. Wang et al., Estimation of the complex-valued mixing matrix by single-source-points detection with less sensors than sources. Trans. Emerg. Telecommun. Technol. 23(2), 137–147 (2012)
X. Luciani, A.L.F. de Almeida, P. Comon, Blind identification of underdetermined mixtures based on the characteristic function: the complex case. IEEE Trans. Signal Process. 59(2), 540–553 (2011)
Y. Moudden, J. Bobin, Hyperspectral BSS using GMCA with spatio-spectral sparsity constraints. IEEE Trans. Image Process. 20(3), 872–879 (2011)
B. Ottersten, T. Kailath, Direction-of-arrival estimation for wide-band signals using the ESPRIT algorithm. IEEE Trans. 38(2), 371–327 (1990)
M. Puigt, Y. Devine, Time–frequency ratio-based blind separation methods for attenuated and time-delayed sources. Mech. Syst. Signal Process. 19(6), 1348–1379 (2005)
V.G. Reju, S.N. Koh, I.Y. Soon, An algorithm for mixing matrix estimation in instantaneous blind source separation. Signal process. 89, 1762–1773 (2009)
B. Tan, S. Xie, Underdetermined blind separation based on source signals’ number estimation. J. Electron. Inf. Technol. (in Chinese) 30(4), 863–867 (2008)
N. Tengtrairat, B. Gao et al., Single-channel blind separation using pseudo-stereo mixture and complex 2-D histogram. IEEE Trans. Neural Netw. 24(11), 1722–1735 (2013)
P. Tichavský, Z. Koldovský, Weight adjusted tensor method for blind separation of underdetermined mixtures of nonstationary sources. IEEE Trans. Signal Process. 59(3), 1037–1047 (2011)
S. Xie, L. Yang, J. Yang et al., Time–frequency approach to underdetermined blind source separation. IEEE Trans. Neural Netw. Learn. Syst. 23(2), 306–316 (2012)
H. Yan, H.H. Fan, Improved cyclic and conjugate cyclic MUSIC. Sens. Array Multichannel Signal Process. Workshop Proc. 4, 289–293 (2004)
O. Yilmaz, S. Richard, Blind separation of speech mixtures via time–frequency masking. IEEE Trans. Signal Process. 52(7), 1830–1847 (2004)
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant Nos. 61172061 and 61201242 and the Natural Science Foundation of JiangSu Province in China under Grant No. BK2012057.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Proof of Theorem 1
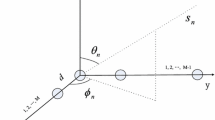
We assume that (t, f) is an SSP of the c-th source. According to the Eqs. (2) and (7), we set \(\alpha _c =-\pi \sin (\theta _c )\) and can obtain:
Observe the diagonal elements and we can get:
That is a condition that SSPs must satisfy. Now we will prove that the condition is strict for other points. We assume that \((t^{\prime },f^{\prime })\) is not the SSP and put the Eqs. (2), (5), (9) into (6) at \((t^{\prime },f^{\prime })\). Then, we will get:
If \((t^{\prime },f^{\prime })\) satisfies the Eq. (16), we will obtain:
If the equation above is permanently equal for arbitrary value of \(\rho _{s_p s_q } (t^{\prime },f^{\prime }),p,q\in \{1,2,\ldots ,N\},p\ne q\), we will get \(\alpha _p =\alpha _q , \quad \forall p, \quad q\in \{1,2,\ldots ,N\},p\ne q\). And \(\alpha _i =-\pi \sin (\theta _i ),i\in \{1,\ldots ,N\}\), so \(\theta _p =\theta _q , \quad \forall p,q\in \{1,2,\ldots ,N\},p\ne q\), it contradicts with the hypothesis \(\theta _i \ne \theta _j (\forall i\ne j)\) that we made before.
A little disturbing point satisfies the Eq. (18), such as the points satisfy the equation below:
where \(\forall p,q\in \{1,2,\ldots ,N\},p\ne q\). In order to satisfy the equation above, there will be a strict condition that is shown below:
The condition is too strict for disturbing points. So far, we do not consider the case with\(\rho _{s_p s_q } (t^{\prime },f^{\prime })=0\), because at disturbing point there will exist many \(p,q\in \{1,2,\ldots ,N\}\) where\(\rho _{s_p s_q } (t^{\prime },f^{\prime })\ne 0\), and these \(p,q\in \{1,\ldots ,N\}\) satisfying (19) is strict all the same.
In conclusion, the Eq. (16) can be served as a criterion to detect the SSPs. But the Eq. (16) must not be satisfied sternly, so we introduce a positive threshold \(\varepsilon _1 \) which is close to 0. The modified criterion can be described by:
This completes the proof of the Theorem 1. \(\square \)
Appendix B
Proof of Theorem 2
We assume that (t, f) is an SSP of the c-th source. According to the Eq. (15), we can obtain M equations:
The M equation above can be written to be a unitary equation:
where \(k=1,2,\ldots ,M\). Then we separate these complexes into real part and imaginary part where \(\rho _{s_c s_c } (t,f)\) and \(\rho _{x_k x_k } (t,f)\) are the real value seen from the Eq. (3).
And we can get:
So we can obtain:
where \(m=1,2,\ldots ,M\). We add the square of the first two equations of (21) together and notice that \(\left| {e^{j(m-k)\alpha _c }} \right| =1\). So, we can obtain:
Equation (22) indicates that \(\left| {\rho _{x_m x_k } (t,f)} \right| \), namely the modulus or the absolute value of mixture signals WVD, are the same for the \(\forall m,k\in \{1,\ldots ,M\}\) including the case that \(m=k\) (that is \(\rho _{x_k x_k } (t,f))\).
That is a condition that SSPs must satisfy. Now we will prove that the condition is strict for other points. We assume that \((t^{\prime },f^{\prime })\) is the disturbing point. From (17), if \((t^{\prime },f^{\prime })\) satisfies the condition in (22), we can obtain:
where \(m,k\in \{1,2,\ldots ,M\},m\ne k\). If we set \(\sum _{q=1}^N {e^{j[(k-1)\alpha _p -(k-1)\alpha _q ]}\rho _{s_p s_q } (t^{\prime },f^{\prime })} =\mathbf{\rho }_p \), (23) will turn to be:
\(\mathbf{\rho }_p \) is arbitrary for different sources. So, it can be inferred that \(\alpha _1 =\alpha _2 =\cdots =\alpha _N \). \(\alpha _i =-\pi \sin (\theta _i ),i\in \{1,2,\ldots ,N\}\), so, \(\theta _p =\theta _q , \quad \forall p,q\in \{1,2,\ldots ,N\},p\ne q\). That is contradictory with the hypothesis that \(\theta _i \ne \theta _j (\forall i\ne j)\). Hence, the condition in (22) is also strict for disturbing points except for a quit few special cases.
Since \(\rho _{x_m x_k } (t,f)\) and \(\rho _{x_k x_m } (t,f)\) are conjugate symmetry, they have the same modulus. So, we can simplify the condition in (22) to be
The selected points may not strictly satisfy (25), so we have to modify (25) to be:
where \(\varepsilon _2 \) is a positive threshold that is close to 0.
From (21), we can get the estimation of DOAs. The phase angle of \(\rho _{x_m x_k } (t,f)\) is same with that of \(e^{j(m-k)\alpha _c }\), namely, \(\mathrm{angle}(\rho _{x_m x_k } (t,f))=(m-k)\alpha _c \) where \(\alpha _c =-\pi \sin (\theta _c ),c\in \{1,2,\ldots ,N\}\). So, we get:
where \(m,k\in \{1,2,\ldots ,M\},m\ne k\). The equation above is the estimation of DOA.
This completes the proof of the Theorem 2. \(\square \)
Rights and permissions
About this article
Cite this article
Su, Q., Shen, Y., Jian, W. et al. Underdetermined Blind Identification for Uniform Linear Array by a New Time–Frequency Method. Circuits Syst Signal Process 36, 99–118 (2017). https://doi.org/10.1007/s00034-016-0292-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-016-0292-9