An Extrapolated Impulse Response Filter Design with Sparse Coefficients Based on a Novel Linear Approximation of Matrix | Circuits, Systems, and Signal Processing Skip to main content
Springer Nature Link
Log in

An Extrapolated Impulse Response Filter Design with Sparse Coefficients Based on a Novel Linear Approximation of Matrix

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

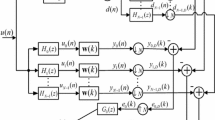
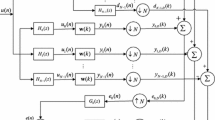
Abstract

A novel method of linear approximation of a matrix is proposed for designing the linear-phase and non-linear-phase extrapolated impulse response (EIR) filters. There are zero-valued and one-valued coefficients in the scale vectors of the proposed EIR filters. These zero-valued coefficients do not require multipliers or adders, and these one-valued coefficients do not require multipliers, in the filter implementation. Additionally, the optimal design of the EIR filters in the mini-max sense and the least-square sense by the iterative gradient searching (IGS) technique is investigated. In implementing the IGS technique, the original EIR filter, the principal component analysis based EIR filter and the proposed EIR filter are set as the initial solutions, separately. If the proposed EIR filter is set as the initial solution, the IGS technique can synthesize the prototype finite impulse response (FIR) filter satisfactorily, with the lowest hardware implementation complexity. Further, experimental comparison of the proposed EIR method with the two most popular non-EIR low-complexity FIR filter design methods also indicates some superiority of the proposed EIR method. Finally, the proposed method of linear approximation of a matrix may also be useful in other areas of signal processing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. J. Adams, A. Willson Jr, A new approach to FIR digital filters with fewer multipliers and reduced sensitivity. IEEE Trans. Circuits Syst. CAS–30, 277–283 (1983)

    Article  Google Scholar 

  2. J. Adams, A. Willson Jr, Some efficient digital prefilter structures. IEEE Trans. Circuits Syst. CAS–31(3), 260–266 (1984)

    Article  Google Scholar 

  3. T. Baran, D. Wei, A.V. Oppenheim, Linear programming algorithms for sparse filter design. IEEE Trans. Signal Process 58(3), 1605–1617 (2010)

    Article  MathSciNet  Google Scholar 

  4. M.R. Bateman, B. Liu, An approach to programmable CTD filters using coefficients 0, +1, and -1. IEEE Trans. Circuits Syst. CAS–27(6), 451–456 (1980)

    Article  Google Scholar 

  5. G.F. Boudreaux, T.W. Parks, Thinning digital filters: A piecewise-exponential approximation approach. IEEE Trans. Acoust. Speech Signal Process. ASSP–31(1), 105–113 (1983)

    Article  Google Scholar 

  6. Y.F. Cao, K. Wang, W.J. Pei, Y.J. Liu, Y.F. Zhang, Design of high order extrapolated impulse response FIR filters with signed power of two coefficients. Circuits Syst. Signal Process. 30(5), 963–985 (2011)

    Article  MathSciNet  Google Scholar 

  7. T.N. Davidson, Enriching the art of FIR filter design via convex optimization. IEEE Signal Process. Mag. 27(3), 89–101 (2010)

    Article  Google Scholar 

  8. M. Grant, S. Boyd, Matlab software for convex programming. http://cvxr.com/cvx/download. Accessed 15 Dec 2014

  9. R.J. Hartnett, G.F. Boudreaux-Bartels, On the use of cyclotomic polynomial prefilters for efficient FIR filter design. IEEE Trans. Signal Process. 41(5), 1766–1779 (1993)

    Article  MATH  Google Scholar 

  10. A.M. Jiang, H.K. Kwan, Y.P. Zhu, X.F. Liu, Minimax design of sparse FIR digital filters. Proc. IEEE ICASSP 2012, 3497–3500 (2012)

    Google Scholar 

  11. A.M. Jiang, H.K. Kwan, Y.P. Zhu, Peak-error-constrained sparse FIR filter design using iterative SOCP. IEEE Trans. Signal Process. 60(8), 4035–4044 (2012)

    Article  MathSciNet  Google Scholar 

  12. F.K.H. Lee, P.J. McLane, Design of nonuniformly-spaced tapped-delay-line equalizers for sparse multipath channels. Proc. IEEE GLOBECOM 2001, 1336–1343 (2001)

    Google Scholar 

  13. Y.C. Lim, Frequency-response masking approach for the synthesis of sharp linear phase digital filters. IEEE Trans. Circuits Syst. CAS–33(4), 357–364 (1986)

    Google Scholar 

  14. Y.C. Lim, B. Liu, Extrapolated impulse response FIR filter. IEEE Trans. Circuits Syst. 37(12), 1548–1551 (1990)

    Article  Google Scholar 

  15. Y.C. Lim, R. Yang, D. Li, J. Song, Signed power-of-two term allocation scheme for the design of digital filters. IEEE Trans. Circuits Syst. II 46(5), 577–584 (1999)

    Article  Google Scholar 

  16. Y.C. Lim, Y.J. Yu, Synthesis of very sharp Hilbert transformer using the frequency-response masking technique. IEEE Trans. Signal Process. 53(7), 2595–2597 (2005)

    Article  MathSciNet  Google Scholar 

  17. J.H. McClellan, T.W. Parks, A personal history of the Parks-McClellan algorithm. IEEE Signal Process. Mag. 22(2), 82–86 (2005)

    Article  Google Scholar 

  18. Y. Neuvo, C.Y. Dong, S.K. Mitra, Interpolated finite impulse response filters. IEEE Trans. Acoust. Speech Signal Process. ASSP–32(3), 563–570 (1984)

    Article  Google Scholar 

  19. W.J. Oh, Y.H. Lee, Design of efficient FIR filters with cyclotomic polynomial prefilters using mixed integer linear programming. IEEE Signal Process. Lett. 3(8), 239–241 (1996)

    Article  Google Scholar 

  20. D. Wei, A.V. Oppenheim, A branch-and-bound algorithm for quadratically constrained sparse filter design. IEEE Trans. Signal Process. 61(4), 1006–1018 (2013)

    Article  MathSciNet  Google Scholar 

  21. H. Wang, L. Zhao, W.J. Pei, J.K. Zuo, Q.Y. Wang, M.H. Xin, An iterative technique for optimally designing extrapolated impulse response filter in the mini-max sense. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E96–A(10), 2029–2033 (2013)

    Article  Google Scholar 

  22. H. Wang, L. Zhao, H.X. Wang, S.L. Fang, P.X. Liu, X.M. Du, An optimal design of the extrapolated impulse response filter with analytical solutions. Signal Process. 92(7), 1665–1672 (2012)

    Article  Google Scholar 

  23. J. Yli-Kaakinen, T. Saramaki, An efficient algorithm for the optimization of FIR filters synthesized using the multistage frequency response masking approach. Circuits Syst. Signal Process. 30(1), 157–183 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  24. Y.J. Yu, G.H. Zhao, K.L. Teo, Y.C. Lim, Optimization of extrapolated impulse response filters using semi-infinite programming. In: Proceedings of First International Symposium on Control, Communications and Signal Processing, pp. 397–400 (2004)

  25. Y.J. Yu, D. Shi, Y.C. Lim, Design of extrapolated impulse response filter with residual compensation in subexpression space. IEEE Trans. Circuits Syst. I 56(12), 2621–2633 (2009)

    Article  MathSciNet  Google Scholar 

  26. Y.J. Yu, K.L. Teo, Y.C. Lim, G.H. Zhao, Extrapolated impulse response filter and its application in the synthesis of digital filters using the frequency-response masking technique. Signal Process. 85(3), 581–590 (2005)

    Article  MATH  Google Scholar 

  27. L.H. Zhou, W.J. Pei, P.C. Xi, Z.Y. He, Extrapolated impulse filter using coefficient-auto-correlation matrix decomposition. Signal Process. 88(7), 1762–1774 (2008)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the anonymous referees and Haixian Wang for constructive recommendations.This work was supported by the Natural Science Foundation of ZhejiangProvince under Grants Nos. LY12F01006 and LY14F010010, the Scientific Research Foundation of Department of Education of Zhejiang Province under Grants No. Y201329723, and the Natural Science Foundation of China under Grant Nos. 61375028, 61273266 and 61301219.

Author information

Authors and Affiliations

  1. School of Communication Engineering, Hangzhou Dianzi University, Hangzhou, 310018, Zhejiang, People’s Republic of China

    Hao Wang

  2. School of Information Science and Engineering, Southeast University, Nanjing, 210096, Jiangsu, People’s Republic of China

    Hao Wang

  3. School of Information Engineering, Huzhou Teachers’ College, Huzhou, 313000, Zhejiang, People’s Republic of China

    Xinmin Cheng & Wenjun Hu

  4. School of Information Science and Engineering, Southeast University, Room 204, Jianxiong Building, Nanjing, 210096, Jiangsu, People’s Republic of China

    Peng Song & Ling Yu

  5. School of Information Science and Engineering, Southeast University, Room 313, Jianxiong Building, Nanjing, 210096, Jiangsu, People’s Republic of China

    Li Zhao

Authors
  1. Hao Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xinmin Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Peng Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ling Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Wenjun Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Li Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hao Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, H., Cheng, X., Song, P. et al. An Extrapolated Impulse Response Filter Design with Sparse Coefficients Based on a Novel Linear Approximation of Matrix. Circuits Syst Signal Process 34, 2335–2361 (2015). https://doi.org/10.1007/s00034-014-9955-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-014-9955-6

Keywords