Abstract
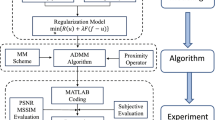
In the field of image processing, total variational model is an effective prior model. In order to better eliminate impulse noise, an effective method is to use \(\ell _{1}{\textit{-norm}}\) total variational model. However, the TV image recovery always produces staircase artifacts, and the \(\ell _{1}{\textit{-norm}}\) excessively penalizes the signal entries. Therefore, in this paper, a new total variational model is proposed to eliminate the staircase effects and impulse noise. We use \(\ell _{0}{\textit{-norm}}\) as the data fidelity term to eliminate impulse noise and the hybrid total variation as the regularization term to effectively eliminate staircase artifacts. In order to effectively tackle the proposed \(\ell _{0}{\textit{-norm}}\) and hybrid total variation, we first express this problem as a Mathematical Program with Equilibrium Constraints(MPEC), and then a Proximal Alternating Direction Method of Multipliers(PADMM) is adopted to solve this problem. In the experimental part, we adopt three indices: \({\textit{SNR}}_{0}\), \({\textit{SNR}}_{1}\) and \({\textit{SNR}}_{2}\) to measure the quality of image restoration. When the value of the \({\textit{SNR}}\) tends to be stable, then each algorithm stops iteration. Numerical simulation results show that the proposed method has better performance in removing impulse noise, suppressing staircase effect and preserving image edge information.






Similar content being viewed by others
References
Tatsugami, F., Higaki, T., Nakamura, Y., et al.: Deep learning-based image restoration algorithm for coronary CT angiography. Eur. Radiol. 29(10), 5322–5329 (2019)
Wang, Z., Zhang, Z., Dong, L., et al.: Jitter detection and image restoration based on generative adversarial networks in satellite images. Sensors 21(14), 4693 (2021)
Li, C., Li, J., Luo, Z.: An impulse noise removal model algorithm based on logarithmic image prior for medical image. Signal Image Video Process. 15, 1145–1152 (2021)
Shi, Y., Zhang, X., Wang, M., et al.: An adaptive non-convex hybrid total variation regularization method for image reconstruction in electrical impedance tomography. Flow Meas. Instrum. 79, 101937 (2021)
Tikhonov, A.N., Arsenn, V.Y.: Solution of Ill-Posed Problem. Winston and Sons, Washington (1977)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60(1–4), 259–268 (1992)
Vogel, C.R., Oman, M.E.: Iterative methods for total variation denoising. SIAM J. Sci. Comput. 17(1), 227–238 (1996)
Chambolle, A., Lions, P.L.: Image recovery via total variation minimization and related problems. Numer. Math. 76(2), 167–188 (1997)
Chan, T., Marquina, A., Mulet, P.: High-order total variation-based image restoration. SIAM J. Sci. Comput. 22(2), 503–516 (2000)
Lv, X.G., Song, Y.Z., Wang, S.X., et al.: Image restoration with a high-order total variation minimization method. Appl. Math. Model. 37(16–17), 8210–8224 (2013)
Zhu, G.J., Li, K., Hao, B.B.: Image restoration by a mixed high-order total variation and l1 regularization model. Math. Probl. Eng. 2018, Article ID 6538610 (2018)
Lysaker, M., Tai, X.C.: Iterative image restoration combining total variation minimization and a second-order functional. Int. J. Comput. Vis. 66(1), 5–18 (2006)
Zhu, J., Li, K., Hao, B.: Restoration of remote sensing images based on nonconvex constrained high-order total variation regularization. J. Appl. Remote Sens. 13(2), 022006 (2019)
You, Y.L., Kaveh, M.: Fourth-order partial differential equations for noise removal. IEEE Trans. Image Process. 9(10), 1723–1730 (2000)
Hajiaboli, M.R.: An anisotropic fourth-order diffusion filter for image noise removal. Int. J. Comput. Vis. 92(2), 177–191 (2011)
Chen, D., Chen, Y.Q., Xue, D.: Fractional-order total variation image denoising based on proximity algorithm. Appl. Math. Comput. 257, 537–545 (2015)
Ren, Z., He, C., Zhang, Q.: Fractional order total variation regularization for image super-resolution. Signal Proess. 93(9), 2408–2421 (2013)
Wu, C., Tai, X.C.: Augmented Lagrangian method, dual methods, and split Bregman iteration for ROF, vectorial TV, and high order models. SIAM J. Imaging Sci. 3(3), 300–339 (2010)
Yan-Yan, Z., Su-Ting, C., Jun-Xiang, G. et al.: Removal of additive noise in adaptive optics system based on adaptive nonconvex sparse regularization. Acta Phys. Sin. 66(12) (2017)
Kuang, S., Chao, H.Y., Yang, J.: Efficient lq norm based sparse subspace clustering via smooth IRLS and ADMM. Multimed. Tools Appl. 76(22), 23163–23185 (2017)
Luo, Z.Q., Pang, J.S., Ralph, D.: Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge (1996)
d’Aspremont, A.: A semidefinite representation for some minimum cardinality problems. In: 42nd IEEE International Conference on Decision and Control, vol. 5, pp. 4985–4990. IEEE (2003)
Feng, M., Mitchell, J.E., Pang, J.S., et al.: Complementarity formulations of l0-norm optimization problems. In: Industrial Engineering and Management Sciences, p. 5. Technical Report. Northwestern University, Evanston, IL, USA (2013)
Yuan, G., Ghanem, B.: \(\ell _0 \) TV: a sparse optimization method for impulse noise image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 41(2), 352–364 (2017)
Acknowledgements
This work is supported in part by the Natural Science Foundation of China under Grant No. 61472003, Academic and Technical Leaders and Backup Candidates of Anhui Province under Grant No. 2019h211, Innovation team of 50 Star of Science and Technology of Huainan, Anhui Province.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, P., Li, D. A new non-convex sparse optimization method for image restoration. SIViP 17, 3829–3836 (2023). https://doi.org/10.1007/s11760-023-02611-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11760-023-02611-1