A novel fourth order chaotic system and its algorithm for medical image encryption | Multidimensional Systems and Signal Processing Skip to main content

Advertisement

Springer Nature Link
Log in

A novel fourth order chaotic system and its algorithm for medical image encryption

  • Original Paper
  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

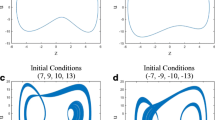
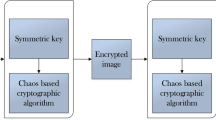
Today, medical imaging suffers from serious issues such as malicious tampering and privacy leakage. Encryption is an effective way to protect these images from security threats. Chaos has been widely used in image encryption, the majority of these algorithms are based on classical chaotic systems. For now, these systems are easy to analyze and predict, which are not sufficient for image encryption proposes. In this paper, a novel fourth order chaotic system is proposed, accompanied by analysis of Lyapunov exponent and bifurcations. Finally, the application of this system with medical image encryption is proposed. As this system could have six control parameters and four initial conditions, the key space is far greater than 5.1 × 218191, which is large enough to resist brute force attack. Correlation analysis and differential attack analysis further demonstrate that this scheme has a strong resistance against statistical attacks and differential attack.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Ahmed, H. U., Bosaily, A. E. S., Brown, L. C., et al. (2017). Diagnostic accuracy of multi-parametric MRI and TRUS biopsy in prostate cancer (PROMIS): A paired validating confirmatory study. The Lancet, 389(10071), 815–822.

    Article  Google Scholar 

  • Albisinni, S., Artigas, C., Aoun, F., et al. (2017). Clinical impact of 68 Ga-prostate-specific membrane antigen (PSMA) positron emission tomography/computed tomography (PET/CT) in patients with prostate cancer with rising prostate-specific antigen after treatment with curative intent: preliminary analysis of a multidisciplinary approach. BJU International, 120(2), 197–203.

    Article  Google Scholar 

  • Arroyo, D., Hernandez, F., & Orúe, A. B. (2017). Cryptanalysis of a classical chaos-based cryptosystem with some quantum cryptography features. International Journal of Bifurcation and Chaos, 27(01), 1750004.

    Article  MATH  Google Scholar 

  • Bruining, D. H., Zimmermann, E. M., Loftus, E. V., Jr., et al. (2018). Consensus recommendations for evaluation, interpretation, and utilization of computed tomography and magnetic resonance enterography in patients with small bowel Crohn’s disease. Gastroenterology, 154(4), 1172–1194.

    Article  Google Scholar 

  • Cao, W., Zhou, Y., Chen, C. L. P., et al. (2017). Medical image encryption using edge maps. Signal Processing, 132, 96–109.

    Article  Google Scholar 

  • Chen, G., Mao, Y., & Chui, C. K. (2004). A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos, Solitons & Fractals, 21(3), 749–761.

    Article  MathSciNet  MATH  Google Scholar 

  • Chen, J., Zhu, Z., Fu, C., et al. (2015). A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Communications in Nonlinear Science and Numerical Simulation, 20(3), 846–860.

    Article  Google Scholar 

  • Fu-Yan, S., Shu-Tang, L., & Zong-Wang, L. (2007). Image encryption using high-dimension chaotic system. Chinese Physics, 16(12), 3616.

    Article  Google Scholar 

  • Ge, R., Zhang, L., Zhang, T., et al. (2016). A modified pulse-coupled spiking neuron circuit with memory threshold and its application. IEICE Electronics Express, 13(8), 20151121.

    Article  Google Scholar 

  • Guo, J. I. (2000). A new chaotic key-based design for image encryption and decryption. In The 2000 IEEE international symposium on proceedings of circuits and systems, 2000, ISCAS 2000 (Vol. 4, pp. 49–52), Geneva. IEEE.

  • Hua, Z., Yi, S., & Zhou, Y. (2018). Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Processing, 144, 134–144.

    Article  Google Scholar 

  • Huang, F., Huang, J., & Shi, Y. Q. (2016). New framework for reversible data hiding in encrypted domain. IEEE Transactions on Information Forensics and Security, 11(12), 2777–2789.

    Article  Google Scholar 

  • Jeng, F. G., Huang, W. L., & Chen, T. H. (2015). Cryptanalysis and improvement of two hyper-chaos-based image encryption schemes. Signal Processing: Image Communication, 34, 45–51.

    Google Scholar 

  • Li, Y., Wang, C., & Chen, H. (2017). A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Optics and Lasers in Engineering, 90, 238–246.

    Article  Google Scholar 

  • Liu, J., Ma, Y., Li, S., et al. (2018a). A new simple chaotic system and its application in medical image encryption. Multimedia Tools and Applications, 77, 22787–22808.

    Article  Google Scholar 

  • Liu, J., Ma, J., Lian, J., et al. (2018b). An approach for the Generation of an nth-order chaotic system with hyperbolic sine. Entropy, 20(4), 230.

    Article  MathSciNet  Google Scholar 

  • Liu, J., Sprott, J. C., Wang, S., et al. (2018c). Simplest chaotic system with a hyperbolic sine and its applications in DCSK scheme. IET Communications, 12(7), 809–815.

    Article  Google Scholar 

  • Liu, H., & Wang, X. (2011). Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Optics Communications, 284(16–17), 3895–3903.

    Article  Google Scholar 

  • Nazarimehr, F., Jafari, S., Golpayegani, S. M. R. H., et al. (2017). Can Lyapunov exponent predict critical transitions in biological systems? Nonlinear Dynamics, 88(2), 1493–1500.

    Article  MathSciNet  Google Scholar 

  • Quader, N., Hodgson, A. J., Mulpuri, K., et al. (2017). Automatic evaluation of scan adequacy and dysplasia metrics in 2-D ultrasound images of the neonatal hip. Ultrasound in Medicine and Biology, 43(6), 1252–1262.

    Article  Google Scholar 

  • Scharinger, J. (1998). Fast encryption of image data using chaotic Kolmogorov flows. Journal of Electronic Imaging, 7(2), 318–325.

    Article  Google Scholar 

  • Sprott, J. C. (2000). A new class of chaotic circuit. Physics Letters A, 266(1), 19–23.

    Article  MathSciNet  Google Scholar 

  • Sprott, J. C. (2003). Chaos and time-series analysis. Oxford: Oxford University Press.

    MATH  Google Scholar 

  • Strogatz, S. H. (2018). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering. Boca Raton: CRC Press.

    Book  MATH  Google Scholar 

  • Tong, X. J., Zhang, M., Wang, Z., et al. (2016). A joint color image encryption and compression scheme based on hyper-chaotic system. Nonlinear Dynamics, 84(4), 2333–2356.

    Article  Google Scholar 

  • Wang, X., & Liu, L. (2013). Cryptanalysis of a parallel sub-image encryption method with high-dimensional chaos. Nonlinear Dynamics, 73(1–2), 795–800.

    Article  MathSciNet  MATH  Google Scholar 

  • Wang, X., & Zhang, H. (2016). A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dynamics, 83(1–2), 333–346.

    Article  MathSciNet  Google Scholar 

  • Yuan, H. M., Liu, Y., Gong, L. H., et al. (2017). A new image cryptosystem based on 2D hyper-chaotic system. Multimedia Tools and Applications, 76(6), 8087–8108.

    Article  Google Scholar 

  • Zhang, X. G., Ma, Y. D., & LI, S. L. (2011). Nonlinear circuit: Based analysis and design. Beijing: Higher Education Press.

    Google Scholar 

  • Zhang, Y., Wen, W., Su, M., et al. (2014). Cryptanalyzing a novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system. Optik-International Journal for Light and Electron Optics, 125(4), 1562–1564.

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Wenlong Xin for providing the knowledge of medical images. All medical images are from First Hospital Affiliated to Lanzhou University. Thanks for proofreading provided by Xiangzi Zhang. Thanks for the useful suggestions provided by Shouliang Li. This study was supported by the Fundamental Research Funds for the Central Universities (No. lzujbky-2016-238). National Natural Science Foundation of China (No. 61175012). 2017 second batch of innovation base and innovative talents (Small and medium enterprises innovation fund 17CX2JA018).

Author information

Authors and Affiliations

  1. School of Information Science and Engineering, Lanzhou University, No. 222, TianShui Road (South), Lanzhou, China

    Jizhao Liu, Shusen Tang, Jing Lian, Yide Ma & Xinguo Zhang

Authors
  1. Jizhao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shusen Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jing Lian
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yide Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xinguo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yide Ma.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, J., Tang, S., Lian, J. et al. A novel fourth order chaotic system and its algorithm for medical image encryption. Multidim Syst Sign Process 30, 1637–1657 (2019). https://doi.org/10.1007/s11045-018-0622-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-018-0622-0

Keywords

Search

Navigation