The block-wise circumcentered–reflection method | Computational Optimization and Applications Skip to main content
Springer Nature Link
Log in

The block-wise circumcentered–reflection method

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

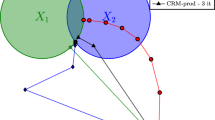
Abstract

The elementary Euclidean concept of circumcenter has recently been employed to improve two aspects of the classical Douglas–Rachford method for projecting onto the intersection of affine subspaces. The so-called circumcentered–reflection method is able to both accelerate the average reflection scheme by the Douglas–Rachford method and cope with the intersection of more than two affine subspaces. We now introduce the technique of circumcentering in blocks, which, more than just an option over the basic algorithm of circumcenters, turns out to be an elegant manner of generalizing the method of alternating projections. Linear convergence for this novel block-wise circumcenter framework is derived and illustrated numerically. Furthermore, we prove that the original circumcentered–reflection method essentially finds the best approximation solution in one single step if the given affine subspaces are hyperplanes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Recent results on Douglas–Rachford methods for combinatorial optimization problems. J. Optim. Theory Appl. 163(1), 1–30 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Aragón Artacho, F.J., Campoy, R., Tam, M.K.: The Douglas–Rachford algorithm for convex and nonconvex feasibility problems. arXiv:1904.09148 (2019)

  3. Bauschke, H.H., Bello-Cruz, J.Y., Nghia, T.T.A., Phan, H.M., Wang, X.: The rate of linear convergence of the Douglas–Rachford algorithm for subspaces is the cosine of the Friedrichs angle. J. Approx. Theory 185, 63–79 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bauschke, H.H., Bello-Cruz, J.Y., Nghia, T.T.A., Phan, H.M., Wang, X.: Optimal rates of linear convergence of relaxed alternating projections and generalized Douglas–Rachford methods for two subspaces. Numer. Algorithms 73(1), 33–76 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bauschke, H.H., Borwein, J.M.: On the convergence of von Neumann’s alternating projection algorithm for two sets. Set-Valued Anal. 1(2), 185–212 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38(3), 367–426 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bauschke, H.H., Deutsch, F.R., Hundal, H., Park, S.H.: Accelerating the convergence of the method of alternating projections. Trans. Am. Math. Soc. 355(9), 3433–3461 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bauschke, H.H., Luke, D.R., Phan, H.M., Wang, X.: Restricted normal cones and the method of alternating projections: theory. Set-Valued Var. Anal. 21(3), 431–473 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bauschke, H.H., Moursi, W.M.: The Douglas–Rachford algorithm for two (not necessarily intersecting) affine subspaces. SIAM J. Optim. 26(2), 968–985 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  10. Bauschke, H.H., Ouyang, H., Wang, X.: On circumcenters of finite sets in Hilbert spaces. Linear Nonlinear Anal. 4(2), 271–295 (2018)

    MathSciNet  Google Scholar 

  11. Bauschke, H.H., Ouyang, H., Wang, X.: Circumcentered methods induced by isometries. arXiv:1908.11576 (2019)

  12. Bauschke, H.H., Ouyang, H., Wang, X.: On circumcenter mappings induced by nonexpansive operators. Pure Appl. Funct. Anal. (in press)

  13. Behling, R., Bello-Cruz, J.Y., Santos, L.R.: Circumcentering the Douglas–Rachford method. Numer. Algorithms 78(3), 759–776 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  14. Behling, R., Bello-Cruz, J.Y., Santos, L.R.: On the linear convergence of the circumcentered–reflection method. Oper. Res. Lett. 46(2), 159–162 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  15. Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: a fresh approach to numerical computing. SIAM Rev. 59(1), 65–98 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  16. Boisvert, R.F., Pozo, R., Remington, K., Barrett, R.F., Dongarra, J.J.: Matrix market: a web resource for test matrix collections. In: Boisvert, R.F. (ed.) Quality of Numerical Software, pp. 125–137. Springer, Boston (1997)

    Chapter  Google Scholar 

  17. Borwein, J.M., Tam, M.K.: A cyclic Douglas–Rachford iteration scheme. J. Optim. Theory Appl. 160(1), 1–29 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Borwein, J.M., Tam, M.K.: The cyclic Douglas–Rachford method for inconsistent feasibility problems. J. Nonlinear Convex Anal. 16(4), 573–584 (2015)

    MathSciNet  MATH  Google Scholar 

  19. Demanet, L., Zhang, X.: Eventual linear convergence of the Douglas–Rachford iteration for basis pursuit. Math. Comput. 85(297), 209–238 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Deutsch, F.R.: The angle between subspaces of a Hilbert space. In: Singh, S.P. (ed.) Approximation Theory, Wavelets and Applications, pp. 107–130. Springer, Dordrecht (1995)

    Chapter  Google Scholar 

  21. Deutsch, F.R.: Best Approximation in Inner Product Spaces. CMS Books in Mathematics. Springer, New York (2001)

    Book  Google Scholar 

  22. Hansen, P.C., Jørgensen, J.S.: AIR tools II: algebraic iterative reconstruction methods, improved implementation. Numer. Algorithms 79(1), 107–137 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Herman, G.T.: Fundamentals of Computerized Tomography, 2 edn. Advances in Pattern Recognition. Springer, Dordrecht (2009)

    Book  Google Scholar 

  24. Hesse, R., Luke, D.R.: Nonconvex notions of regularity and convergence of fundamental algorithms for feasibility problems. SIAM J. Optim. 23(4), 2397–2419 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hesse, R., Luke, D.R., Neumann, P.: Alternating projections and Douglas–Rachford for sparse affine feasibility. IEEE Trans. Signal Process. 62(18), 4868–4881 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  26. Lindstrom, S.B., Sims, B.: Survey: sixty years of Douglas–Rachford. arXiv:1809.07181 (2018)

  27. Ouyang, H.: Circumcenter operators in Hilbert spaces. Master’s Thesis, University of British Columbia, Okanagan (2018)

  28. Shepp, L.A., Logan, B.F.: The fourier reconstruction of a head section. IEEE Trans. Nucl. Sci. 21(3), 21–43 (1974)

    Article  Google Scholar 

  29. Strohmer, T., Vershynin, R.: A randomized Kaczmarz algorithm with exponential convergence. J. Fourier Anal. Appl. 15(2), 262–278 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We dedicate this paper in honor of the 70th birthday of Professor J. M. Martínez and of the 60th birthday of Professor Yuan Jinyun. The first author wants to thank the Federal University of Santa Catarina and remarks that part of his contribution to the present work was carried out at this institution. We thank the anonymous referees for their valuable suggestions which significantly improved the presentation of this manuscript.

Author information

Authors and Affiliations

  1. School of Applied Mathematics, Fundação Getúlio Vargas, Rio de Janeiro, RJ, 22250-900, Brazil

    Roger Behling

  2. Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL, 60115-2828, USA

    J.-Yunier Bello-Cruz

  3. Department of Mathematics, Federal University of Santa Catarina, Blumenau, SC, 88040-900, Brazil

    Luiz-Rafael Santos

Authors
  1. Roger Behling
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J.-Yunier Bello-Cruz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Luiz-Rafael Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Roger Behling.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

RB was partially supported by Brazilian Agency Conselho Nacional de Pesquisa (CNPq), Grants 304392/2018-9 and 429915/2018-7; JYBC was partially supported by the National Science Foundation (NSF), Grant DMS—1816449.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Behling, R., Bello-Cruz, JY. & Santos, LR. The block-wise circumcentered–reflection method. Comput Optim Appl 76, 675–699 (2020). https://doi.org/10.1007/s10589-019-00155-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-019-00155-0

Keywords

Mathematics Subject Classification

Search

Navigation