Density-based IFCM along with its interval valued and probabilistic extensions, and a review of intuitionistic fuzzy clustering methods | Artificial Intelligence Review
Skip to main content
Springer Nature Link
Log in

Density-based IFCM along with its interval valued and probabilistic extensions, and a review of intuitionistic fuzzy clustering methods

  • Published:
Artificial Intelligence Review Aims and scope Submit manuscript

Abstract

Fuzzy clustering has been useful in capturing the uncertainty present in the data during clustering. Most of the c-Means algorithms such as FCM (Fuzzy c-Means), IFCM (Intuitionistic Fuzzy c-Means), and the recently reported PIFCM (Probabilistic Intuitionistic Fuzzy c-means) randomly initialize cluster centroids. Performance of these techniques is very reliant on the initialized cluster centroids. So, a good initialization technique can significantly affect the cluster formation. Recently, density-based initialization technique for FCM (DFCM) was proposed, which initializes datapoints with high density as cluster centroids. In DFCM, points within some distance contribute in the density of the data points. In this paper, we propose a new way to compute fuzzy density of datapoints based on the distance measure. Uncertainty can be better captured by intuitionistic fuzzy set (IFS) and interval-valued IFS (IVIFS). Thus, we propose a new density-based initialization technique for IFCM, called ‘Density based Intuitionistic Fuzzy c-Means (DIFCM) Algorithm’. The proposed DIFCM has been further developed for IVIFS, which we term ‘Interval-valued Density based Intuitionistic Fuzzy c-Means (IVDIFCM) Algorithm’, is also introduced in this paper. PIFCM incorporates probabilistic weights between membership, non-membership and hesitancy component. In this paper, we also introduce the density based initialized cluster centroids for PIFCM algorithm to propose the ‘Density Based Probabilistic Intuitionistic Fuzzy c-Means (DPIFCM) Algorithm’. There were many clustering approaches based on IFSs but there do not exist any literature review on the IFS based clustering approaches. Therefore,  this article also provides a detailed review of the recently proposed clustering algorithms based on IFS theory. Experiments over various UCI datasets proves that our proposed algorithms has better clustering results than their existing counterparts.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

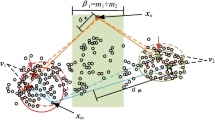
  1. Since the Seed data set and the Wine dataset have more than two dimensions, there are some overlapping points belonging to different classes as they are significantly different for other dimensions.

References

  • Ananthi VP, Balasubramaniam P, Kalaiselvi T (2016) A new fuzzy clustering algorithm for the segmentation of brain tumor.". Soft Comput 20(12):4859–4879

    Article  Google Scholar 

  • Arora J, Tushir M (2020) An enhanced spatial intuitionistic fuzzy C-means clustering for image segmentation. Procedia Comput Sci 167:646–655

    Article  Google Scholar 

  • A.Asuncion D. Newman (2007) UCI machine learning repository

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    Article  MathSciNet  MATH  Google Scholar 

  • Atanassov KT (1999) Interval valued intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets, Physica, Heidelberg

    Book  MATH  Google Scholar 

  • Bai X, Zhang Y, Liu H, Wang Y (2018a) Intuitionistic center-free FCM clustering for MR brain image segmentation. IEEE J Biomed Health Inform 23(5):2039–2051

    Article  Google Scholar 

  • Bai X, Sun C, Sun C (2018b) Cell segmentation based on FOPSO combined with shape information improved intuitionistic FCM. IEEE J Biomed Health Inform 23(1):449–459

    Article  Google Scholar 

  • Balafar MA (2014) Fuzzy C-mean based brain MRI segmentation algorithms. Artif Intell Rev 41(3):441–449

    Article  Google Scholar 

  • Baraldi A, Blonda P (1999) A survey of fuzzy clustering algorithms for pattern recognition. IEEE Transact Syst, Man, and Cybernetics, Part B 29(6):778–785

    Article  Google Scholar 

  • Bataineh KM, Naji M, Saqer M (2011) A Comparison study between various fuzzy clustering algorithms. Jordan J Mech Industrial Eng 5:4

    Google Scholar 

  • Bezdek JC (2013) Pattern recognition with fuzzy objective function algorithms. Springer Science & Business Media, Cham

    MATH  Google Scholar 

  • Bezdek JC, Ehrlich R, Full W (1984) FCM: The fuzzy c-means clustering algorithm. Comput Geosci 10(2–3):191–203

    Article  Google Scholar 

  • Cai W, Chen S, Zhang D (2007) Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recogn 40(3):825–838

    Article  MATH  Google Scholar 

  • Chaira T (2011) A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl Soft Comput 11(2):1711–1717

    Article  Google Scholar 

  • Chaira T (2012) Intuitionistic fuzzy color clustering of human cell images on different color models. J Intell Fuzzy Syst 23(2):43–51

    Article  MathSciNet  MATH  Google Scholar 

  • Chaira T, Panwar A (2014) An Atanassov’s intuitionistic fuzzy kernel clustering for medical image segmentation. Int J Comput Intell Sys 7(2):360–370

    Article  Google Scholar 

  • Chen S-M (1995) Measures of similarity between vague sets. Fuzzy Sets Syst 74(2):217–223

    Article  MathSciNet  MATH  Google Scholar 

  • Chen X, Li Di, Wang X, Yang X, Li H (2018) Rough intuitionistic type-2 fuzzy c-means clustering algorithm for MR image segmentation. IET Image Proc 13(4):607–614

    Article  Google Scholar 

  • Cheriton D, Tarjan RE (1976) Finding minimum spanning trees. SIAM J Comput 5(4):724–742

    Article  MathSciNet  MATH  Google Scholar 

  • Cuong BC, Lanzi PL, Thong NT (2012) A novel intuitionistic fuzzy clustering method for geo-demographic analysis. Expert Syst Appl 39(10):9848–9859

    Article  Google Scholar 

  • Ding, Jundi, Runing Ma, Xiaoqing Hu, Jingyu Yang, and Songcan Chen (2010) Fuzzy c-means revisited: Towards a cluster-center-free reformulation. In 2010 Chinese Conference on Pattern Recognition (CCPR), pp. 1–5. IEEE

  • Dubey YK, Mushrif MM, Mitra K (2016) Segmentation of brain MR images using rough set based intuitionistic fuzzy clustering. Biocybernetics Biomed Eng 36(2):413–426

    Article  Google Scholar 

  • Dubois D, Prade H (1990) Rough fuzzy sets and fuzzy rough sets. Int J General Syst 17(2–3):191–209

    Article  MATH  Google Scholar 

  • Elazab A, Wang C, Jia F, Jianhuang Wu, Li G, Qingmao Hu (2015) Segmentation of brain tissues from magnetic resonance images using adaptively regularized kernel-based fuzzy-means clustering. Comput Mathemat Methods Med 2015:1–12

    Article  MATH  Google Scholar 

  • Ester M, Kriegel HP, Sander J, Xu X (1996) A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 96(34):226–231

    Google Scholar 

  • Ferraro MB, Giordani P (2019) A review and proposal of (fuzzy) clustering for nonlinearly separable data. Int JApproximate Reasoning 115:13–31

    Article  MathSciNet  MATH  Google Scholar 

  • Gao, Zhe, Junxiu Wei, Chao Liang, and Ming Yan (2014) Fractional-order particle swarm optimization. In The 26th Chinese Control and Decision Conference (2014 CCDC), pp. 1284–1288. IEEE

  • Guijun W, Xiaoping L (1998) The applications of interval-valued fuzzy numbers and interval-distribution numbers. Fuzzy Sets Syst 98(3):331–335

    Article  MathSciNet  MATH  Google Scholar 

  • Hartigan JA, Wong MA (1979) Algorithm AS 136: A k-means clustering algorithm. J Royal Statist Soc 28(1):100–108

    MATH  Google Scholar 

  • Höppner F, Klawonn F, Kruse R, Runkler T (1999) Fuzzy cluster analysis: methods for classification, data analysis and image recognition. John Wiley & Sons

    MATH  Google Scholar 

  • Hwang C, Rhee F-H (2007) Uncertain fuzzy clustering: Interval type-2 fuzzy approach to c- means. IEEE Trans Fuzzy Syst 15(1):107–120

    Article  Google Scholar 

  • Jati A, Singh G, Koley S, Konar A, Ray AK, Chakraborty C (2015) A novel segmentation approach for noisy medical images using Intuitionistic fuzzy divergence with neighbourhood-based membership function. J Microsc 257(3):187–200

    Article  Google Scholar 

  • Jin, D., & Bai, X. (2019) Distribution information based intuitionistic fuzzy clustering for infrared ship segmentation. IEEE Transactions on Fuzzy Systems

  • Jun Li, Wei-xin X, Liang-qun Li (2017) Online visual multiple target tracking by intuitionistic fuzzy data association. Int J Fuzzy Syst 19(2):355–366

    Article  MathSciNet  Google Scholar 

  • Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J Global Optim 39(3):459–471

    Article  MathSciNet  MATH  Google Scholar 

  • Kaur P, Soni AK, Gosain A (2013) RETRACTED: A robust kernelized intuitionistic fuzzy c-means clustering algorithm in segmentation of noisy medical images. Pattern Recognition Lett 34:163–175

    Article  Google Scholar 

  • Kaur, Prabhjot, A. K. Soni, and Anjana Gosain (2011) Robust Intuitionistic Fuzzy C-means clustering for linearly and nonlinearly separable data. In 2011 International Conference on Image Information Processing, pp. 1–6. IEEE

  • Kong J, Hou J, Jiang M, Sun J (2019) A novel image segmentation method based on improved intuitionistic Fuzzy C-Means clustering algorithm. TIIS 13(6):3121–3143

    Google Scholar 

  • Krinidis S, Chatzis V (2010) A robust fuzzy local information C-means clustering algorithm. IEEE Trans Image Process 19(5):1328–1337

    Article  MathSciNet  MATH  Google Scholar 

  • Kruskal JB (1956) On the shortest spanning subtree of a graph and the traveling salesman problem. Proc Am Mathematical Soc 7(1):48–50

    Article  MathSciNet  MATH  Google Scholar 

  • Kumar D, Verma H, Mehra A, Agrawal RK (2019a) A modified intuitionistic fuzzy c-means clustering approach to segment human brain MRI image. Multimedia Tools and Applications 78(10):12663–12687

    Article  Google Scholar 

  • Kumar D, Verma H, Mehra A, Agrawal RK (2019b) A modified intuitionistic fuzzy c-means clustering approach to segment human brain MRI image. Multimedia Tools and Appl 78(10):12663–12687

    Article  Google Scholar 

  • Kumar D, Agrawal RK, Verma H (2020) Kernel intuitionistic fuzzy entropy clustering for MRI image segmentation. Soft Comput 24(6):4003–4026

    Article  Google Scholar 

  • Kuo RJ, Lin TC, Zulvia FE, Tsai CY (2018) A hybrid metaheuristic and kernel intuitionistic fuzzy c-means algorithm for cluster analysis. Appl Soft Comput 67:299–308

    Article  Google Scholar 

  • Lei, Xiujuan, Fang-Xiang Wu, Jianfang Tian, and Jie Zhao (2014) ABC and IFC: Modules detection method for PPI network. BioMed research international 2014

  • Lin K-P (2013) A novel evolutionary kernel intuitionistic fuzzy c -means clustering algorithm. IEEE Trans Fuzzy Syst 22(5):1074–1087

    Article  Google Scholar 

  • Liu, Meiju, Xiaozheng Yu, and Yixuan Shi (2021) IFCM clustering segmentation based on genetic algorithm. In 2021 33rd Chinese Control and Decision Conference (CCDC), pp. 7379–7384. IEEE

  • Lohani QMD, Solanki R, Muhuri PK (2018a) Novel adaptive clustering algorithms based on a probabilistic similarity measure over atanassov intuitionistic fuzzy set. IEEE Trans Fuzzy Syst 26(6):3715–3729

    Article  Google Scholar 

  • Lohani QMD, Solanki R, Muhuri PK (2018b) A convergence theorem and an experimental study of intuitionistic fuzzy c-mean algorithm over machine learning dataset. Appl Soft Comput 71:1176–1188

    Article  Google Scholar 

  • Mason, G. A., and R. D. Jacobson (2007) Fuzzy geographically weighted clustering. In Proceedings of the 9th International Conference on Geocomputation, no. 1998, pp. 1–7

  • Mayor G (1994) Sugeno’s negations and t-norms. Mathware Soft Comput 1:93–98

    MathSciNet  MATH  Google Scholar 

  • Mirkin B (2013) Mathematical classification and clustering. Springer Science & Business Media, Cham

    MATH  Google Scholar 

  • Namburu A, Samayamantula SK, Edara SR (2017) Generalised rough intuitionistic fuzzy c-means for magnetic resonance brain image segmentation. IET Image Proc 11(9):777–785

    Article  Google Scholar 

  • Nguyen, Dzung Dinh, Long Thanh Ngo, and Long The Pham. "Interval type-2 fuzzy c-means clustering using intuitionistic fuzzy sets." In 2013 Third World Congress on Information and Communication Technologies (WICT 2013), pp. 299–304. IEEE, 2013.

  • Ozcan, Ender, and Chilukuri K. Mohan (1999) Particle swarm optimization: surfing the waves. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), 3: 1939–1944.

  • Pal NR, Bezdek JC (1995) On cluster validity for the fuzzy c-means model. IEEE Trans Fuzzy Syst 3(3):370–379

    Article  Google Scholar 

  • Pal NR, Pal K, Keller JM, Bezdek JC (2005) A possibilistic fuzzy c-means clustering algorithm. IEEE Trans Fuzzy Syst 13(4):517–530

    Article  Google Scholar 

  • Pei HX, Zheng ZR, Wang C, Li CN, Shao YH (2017) D-FCM: Density based fuzzy c-means clustering algorithm with application in medical image segmentation. Procedia Computer Science 122:407–414

    Article  Google Scholar 

  • Pelekis N, Kopanakis I, Kotsifakos EE, Frentzos E, Theodoridis Y (2011) Clustering uncertain trajectories. Knowl Inf Syst 28(1):117–147

    Article  Google Scholar 

  • Pham DL (2001) Spatial models for fuzzy clustering. Comput vis Image Underst 84(2):285–297

    Article  MATH  Google Scholar 

  • Prim RC (1957) Shortest connection networks and some generalizations. The Bell System Technical Journal 36(6):1389–1401

    Article  Google Scholar 

  • Rdusseeun, L. K. P. J. (1987) Clustering by means of medoids

  • Ruspini EH, Bezdek JC, Keller JM (2019) Fuzzy clustering: a historical perspective. IEEE Comput Intell Mag 14(1):45–55

    Article  Google Scholar 

  • Shang, Ronghua, Pingping Tian, Ailing Wen, Wenzhan Liu, and Licheng Jiao. An intuitionistic fuzzy possibilistic C-means clustering based on genetic algorithm In 2016 IEEE Congress on Evolutionary Computation (CEC), pp. 941–947. IEEE, 2016.

  • Srivastava RK, Leone RP, Shocker AD (1981) Market structure analysis: hierarchical clustering of products based on substitution-in-use. J Mark 45(3):38–48

    Article  Google Scholar 

  • Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst 114(3):505–518

    Article  MathSciNet  MATH  Google Scholar 

  • Tasoulis SK, Maglogiannis I, Plagianakos VP (2014) Fractal analysis and fuzzy c-means clustering for quantification of fibrotic microscopy images. Artif Intell Rev 42(3):313–329

    Article  Google Scholar 

  • Thakur N, Juneja M (2019) Optic disc and optic cup segmentation from retinal images using hybrid approach. Expert Syst Appl 127:308–322

    Article  Google Scholar 

  • Trinh C, Huynh B, Bidaki M, Rahmani AM, Hosseinzadeh M, Masdari M (2021) Optimized fuzzy clustering using moth-flame optimization algorithm in wireless sensor networks. Artif Intell Rev 2021:1–31

    Google Scholar 

  • Varshney AK, Muhuri PK, Danish Lohani QM (2022) PIFHC: the probabilistic intuitionistic fuzzy hierarchical clustering algorithm. Appl Soft Comput 120:108584

    Article  Google Scholar 

  • Varshney, Ayush K., QM Danish Lohani, and Pranab K. Muhuri (2020a) Improved probabilistic intuitionistic fuzzy c-Means clustering algorithm: improved PIFCM. In 2020a IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp. 1–6. IEEE

  • Varshney, Ayush K., Priyanka Mehra, Pranab K. Muhuri, and QM Danish Lohani. Interval-Valued Fuzzy c-Means Algorithm and Interval-Valued Density-Based Fuzzy c-Means Algorithm. In 2020b IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp. 1–6. IEEE, 2020b

  • Verma H, Agrawal RK (2015) Possibilistic intuitionistic fuzzy c-means clustering algorithm for MRI brain image segmentation. Int J Artificial Intelligence Tools 24(05):1550016

    Article  Google Scholar 

  • Verma H, Agrawal RK, Sharan A (2016) An improved intuitionistic fuzzy c-means clustering algorithm incorporating local information for brain image segmentation. Appl Soft Comput 46:543–557

    Article  Google Scholar 

  • Verma H, Gupta A, Kumar D (2019) A modified intuitionistic fuzzy c-means algorithm incorporating hesitation degree. Pattern Recogn Lett 122:45–52

    Article  Google Scholar 

  • Visalakshi N, Karthikeyani KT, Parvathi R (2010) An intuitionistic fuzzy approach to distributed fuzzy clustering. Int J Comp Theory Eng 2(2):295

    Article  Google Scholar 

  • Visalakshi N, Karthikeyani SP, Thangavel K (2014) An intuitionistic fuzzy approach to fuzzy clustering of numerical dataset. Computational Intelligence, Cyber Security and Computational Models. Springer, New Delhi, pp 79–87

    Chapter  Google Scholar 

  • Wang W, Xin X (2005) Distance measure between intuitionistic fuzzy sets Pattern Recognit. Lett 26(13):2063–2069

    Google Scholar 

  • Whitley D, Starkweather T (1990) Genitor II: A distributed genetic algorithm. J Exp Theor Artif Intell 2(3):189–214

    Article  Google Scholar 

  • Wu W-Z, Mi J-S, Zhang W-X (2003) Generalized fuzzy rough sets. Inf Sci 151:263–282

    Article  MathSciNet  MATH  Google Scholar 

  • Wu H, Yuyuan Wu, Luo J (2009) An interval type-2 fuzzy rough set model for attribute reduction. IEEE Trans Fuzzy Syst 17(2):301–315

    Article  Google Scholar 

  • Xian S, Yin Y, Liu Y, You M, Wang K (2019) Intuitionistic fuzzy linguistic clustering algorithm based on a new correlation coefficient for intuitionistic fuzzy linguistic information. Pattern Anal Appl 22(3):907–918

    Article  MathSciNet  Google Scholar 

  • Xu Z, Wu J (2010) Intuitionistic fuzzy c-means clustering algorithms. J Syst Eng Electron 21(4):580–590

    Article  Google Scholar 

  • Xu Z, Chen J, Junjie Wu (2008) Clustering algorithm for intuitionistic fuzzy sets. Inf Sci 178(19):3775–3790

    Article  MathSciNet  MATH  Google Scholar 

  • Yager RR (1979) On the measure of fuzziness and negation. Part I: Membership in the unit interval. Int J Gen Syst 5:221–229

    Article  MATH  Google Scholar 

  • Yager RR (1980) On the measure of fuzziness and negation. II. lattices. Inf Control 44(3):236–260

    Article  MathSciNet  MATH  Google Scholar 

  • Yugander, P., Babu J. Sheshagiri, K. Sunanda, and E. Susmitha. Multiple kernel fuzzy C-means algorithm with ALS method for satellite and medical image segmentation. In 2012 International Conference on Devices, Circuits and Systems (ICDCS), pp. 244–248. IEEE, 2012

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    Article  MATH  Google Scholar 

  • Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning-III. Inf Sci 9(1):43–80

    Article  MathSciNet  MATH  Google Scholar 

  • Zang W, Zhang W, Zhang W, Liu X (2017) A kernel-based intuitionistic fuzzy C-Means clustering using a DNA genetic algorithm for magnetic resonance image segmentation. Entropy 19(11):578

    Article  Google Scholar 

  • Zeng S, Wang Z, Huang R, Chen L, Feng D (2019) A study on multi-kernel intuitionistic fuzzy C-means clustering with multiple attributes. Neurocomputing 335:59–71

    Article  Google Scholar 

  • Zeshui Xu (2009) Intuitionistic fuzzy hierarchical clustering algorithms. J Syst Eng Electron 20(1):90–97

    Google Scholar 

  • Zhao H, Zeshui Xu, Liu S, Wang Z (2012) Intuitionistic fuzzy MST clustering algorithms. Comput Ind Eng 62(4):1130–1140

    Article  Google Scholar 

  • Zhao F, Liu H, Fan J, Chen CW, Lan R, Li Na (2018) Intuitionistic fuzzy set approach to multi-objective evolutionary clustering with multiple spatial information for image segmentation. Neurocomputing 312:296–309

    Article  Google Scholar 

  • Zhao F, Chen Y, Liu H, Fan J (2019) Alternate PSO-based adaptive interval type-2 intuitionistic fuzzy C-means clustering algorithm for color image segmentation. IEEE Access 7:64028–64039

    Article  Google Scholar 

  • Zhou X, Zhao R, Fengquan Yu, Tian H (2016) Intuitionistic fuzzy entropy clustering algorithm for infrared image segmentation. J Intell Fuzzy Syst 30(3):1831–1840

    Article  MATH  Google Scholar 

  • Zhou X, Zhang R, Wang X, Huang T, Yang C (2020) Kernel intuitionistic fuzzy c-means and state transition algorithm for clustering problem. Soft Comput 24(20):15507–15518.

Download references

Acknowledgments

Authors are thankful to the editors and the reviewers for all their valuable comments which have helped a lot in improving the work. First author gratefully acknowledges the financial assistance obtained from South Asian University (SAU), New Delhi, India in the form of a master’s scholarship. All authors are also thankful to the SAU, New Delhi for providing the infrastructural facilities to conduct this research through the Computational Intelligence research lab.

Funding

South Asian University.

Author information

Author notes

  1. Ayush K. Varshney

    Present address: Department of Computing Science, Umeå University 90187, Umea, Sweden

Authors and Affiliations

  1. Department of Computer Science, South Asian University, New Delhi, 110021, India

    Ayush K. Varshney & Pranab K. Muhuri

  2. Department of Mathematics, South Asian University, New Delhi 110021, India

    Q. M. Danish Lohani

Authors
  1. Ayush K. Varshney
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pranab K. Muhuri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Q. M. Danish Lohani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pranab K. Muhuri.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Varshney, A.K., Muhuri, P.K. & Lohani, Q.M.D. Density-based IFCM along with its interval valued and probabilistic extensions, and a review of intuitionistic fuzzy clustering methods. Artif Intell Rev 56, 3755–3795 (2023). https://doi.org/10.1007/s10462-022-10236-y

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10462-022-10236-y

Keywords

Search

Navigation