Optimal lifetime consumption and investment under a drawdown constraint | Finance and Stochastics Skip to main content
Springer Nature Link
Log in

Optimal lifetime consumption and investment under a drawdown constraint

  • Published:
Finance and Stochastics Aims and scope Submit manuscript

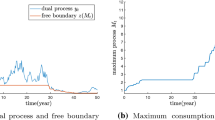
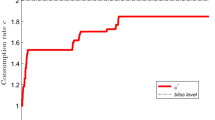
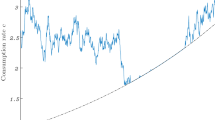
Abstract

We consider the infinite-horizon optimal consumption-investment problem under a drawdown constraint, i.e., when the wealth process never falls below a fixed fraction of its running maximum. We assume that the risky asset is driven by the with constant coefficients. For a general class of utility functions, we provide the value function in explicit form and derive closed-form expressions for the optimal consumption and investment strategy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barles, G., Daher, C., Romano, M.: Optimal control of the \(\mathbb{L}^{\infty}\) -norm of a diffusion process. SIAM J. Control Optim. 32, 612–634 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  2. Ben Tahar, I., Soner, M., Touzi, N.: Modelling continuous-time financial markets with capital gains taxes. Preprint (2005). http://www.cmap.polytechnique.fr/~touzi/bst06.pdf

  3. Constantinides, G.M., Magill, M.J.P.: Portfolio selection with transaction costs. J. Econ. Theory 13, 245–263 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  4. Cox, J., Huang, C.F.: Optimal consumption and portfolio policies when asset prices follow a diffusion process. J. Econ. Theory 49, 33–83 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  5. Cvitanić, J., Karatzas, I.: Convex duality in constrained portfolio optimization. Ann. Appl. Probab. 2, 767–818 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cvitanić, J., Karatzas, I.: On portfolio optimization under “drawdown” constraints. IMA Vol. Math. Appl. 65, 35–46 (1995)

    Google Scholar 

  7. Davis, M.H.A., Norman, A.R.: Portfolio selection with transaction costs. Math. Oper. Res. 15, 676–713 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  8. El Karoui, N., Jeanblanc, M.: Optimization of consumption with labor income. Finance Stoch. 2, 409–440 (1998)

    Article  MATH  Google Scholar 

  9. Grossman, S.J., Zhou, Z.: Optimal investment strategies for controlling drawdowns. Math. Finance 3, 241–276 (1993)

    Article  MATH  Google Scholar 

  10. He, H.: Pagès, H.: Labor income, borrowing constraints and equilibrium asset prices. Econ. Theory 3, 663–696 (1993)

    Article  MATH  Google Scholar 

  11. Karatzas, I., Shreve, S.E.: Brownian Motion and Stochastic Calculus. Springer, New York (1991)

    MATH  Google Scholar 

  12. Karatzas, I., Shreve, S.E.: Methods of Mathematical Finance. Springer, New York (1998)

    MATH  Google Scholar 

  13. Karatzas, I., Lehoczky, J.P., Shreve, S.E.: Optimal portfolio and consumption decisions for a “small investor” on a finite horizon. SIAM J. Control Optim. 25, 1557–1586 (1997)

    Article  MathSciNet  Google Scholar 

  14. Klass, M.J., Nowicki, K.: The Grossman and Zhou investment strategy is not always optimal. Statist. Probab. Lett. 74, 245–252 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  15. Kramkov, D., Schachermayer, W.: The asymptotic elasticity of utility functions and optimal investment in incomplete markets. Ann. Appl. Probab. 9, 904–950 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  16. Merton, R.C.: Lifetime portfolio selection under uncertainty: the continuous-time model. Rev. Econ. Stud. 51, 247–257 (1969)

    Article  Google Scholar 

  17. Merton, R.C.: Optimum consumption and portfolio rules in a continuous-time model. J. Econ. Theory 3, 373–413 (1971)

    Article  MathSciNet  Google Scholar 

  18. Protter, P.: Stochastic Integration and Differential Equations. Springer, Berlin (1990)

    MATH  Google Scholar 

  19. Roche, H.: Optimal consumption and investment strategies under wealth ratcheting. Preprint (2006). http://ciep.itam.mx/~hroche/Research/MDCRESFinal.pdf

  20. Shreve, S.E., Soner, H.M.: Optimal investment and consumption with transaction costs. Ann. Appl. Probab. 4, 609–692 (1994)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. CEREMADE & CREST, Paris, France

    Romuald Elie

  2. Centre de Mathématiques Appliquées, Ecole Polytechnique Paris, Paris, France

    Nizar Touzi

Authors
  1. Romuald Elie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nizar Touzi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Romuald Elie.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Elie, R., Touzi, N. Optimal lifetime consumption and investment under a drawdown constraint. Finance Stoch 12, 299–330 (2008). https://doi.org/10.1007/s00780-008-0066-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00780-008-0066-8

Keywords

Mathematics Subject Classification (2000)

JEL Classification

Search

Navigation