The Number of Independent Sets in a Graph with Small Maximum Degree

Abstract

Let ind(G) be the number of independent sets in a graph G. We show that if G has maximum degree at most 5 then

$${\rm ind}(G) \leq 2^{{\rm iso}(G)} \prod_{uv \in E(G)} {\rm ind}(K_{d(u),d(v)})^{\frac{1}{d(u)d(v)}}$$

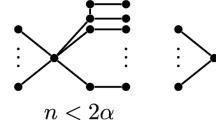
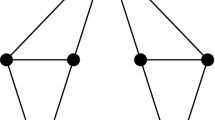
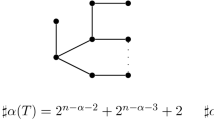
(where d(·) is vertex degree, iso(G) is the number of isolated vertices in G and K _a,b is the complete bipartite graph with a vertices in one partition class and b in the other), with equality if and only if each connected component of G is either a complete bipartite graph or a single vertex. This bound (for all G) was conjectured by Kahn. A corollary of our result is that if G is d-regular with 1 ≤ d ≤ 5 then

$${\rm ind}(G) \leq \left(2^{d+1}-1\right)^\frac{|V(G)|}{2d},$$

with equality if and only if G is a disjoint union of |V(G)|/2d copies of K _d,d. This bound (for all d) was conjectured by Alon and Kahn and recently proved for all d by the second author, without the characterization of the extreme cases. Our proof involves a reduction to a finite search. For graphs with maximum degree at most 3 the search could be done by hand, but for the case of maximum degree 4 or 5, a computer is needed.