A Variational Model for Dislocations at Semi-coherent Interfaces | Journal of Nonlinear Science Skip to main content
Springer Nature Link
Log in

A Variational Model for Dislocations at Semi-coherent Interfaces

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

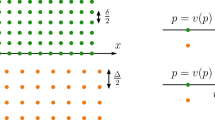
We propose and analyze a simple variational model for dislocations at semi-coherent interfaces. The energy functional describes the competition between two terms: a surface energy induced by dislocations and a bulk elastic energy, spent to decrease the amount of dislocations needed to compensate the lattice misfit. We prove that, for minimizers, the former scales like the surface area of the interface, the latter like its diameter. The proposed continuum model is built on some explicit computations done in the framework of the semi-discrete theory of dislocations. Even if we deal with finite elasticity, linearized elasticity naturally emerges in our analysis since the far-field strain vanishes as the interface size increases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Agostiniani, V., Dal Maso, G., DeSimone, A.: Linear elasticity obtained from finite elasticity by \({\Gamma }\)-convergence under weak coerciveness conditions. Ann. Inst. H. Poincaré Anal. nonlinéaire. 29(5), 715–735 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Alicandro, R., Palombaro, M., Lazzaroni, G.: Derivation of a rod theory from lattice systems with interactions beyond nearest neighbours. http://cvgmt.sns.it/paper/3248/, Preprint (2016)

  • Conti, S., Garroni, A., Müller, S.: The line-tension approximation as the dilute limit of linear-elastic dislocations. Arch. Ration. Mech. Anal. 218, 699–755 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  • Dal Maso, G., Negri, M., Percivale, D.: Linearized elasticity as \(\Gamma \)-limit of finite elasticity. Set-Valued Anal. 10(2–3), 165–183 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  • De Luca, L., Garroni, A., Ponsiglione, M.: \(\Gamma \)-convergence analysis of systems of edge dislocations: the self energy regime. Arch. Ration. Mech. Anal. 206(3), 885–910 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Ernst, F.: Metal-oxide interfaces. Mat. Sci. Eng. R. 14, 97–156 (1995)

    Article  Google Scholar 

  • Fonseca, I., Fusco, N., Leoni, G., Morini, M.: A model for dislocations in epitaxially strained elastic films. Preprint (2016)

  • Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55(11), 1461–1506 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  • Hirsch, P.B.: Nucleation and propagation of misfits dislocations in strained epitaxial layer systems. In: Proceedings of the Second International Conference Schwäbisch Hall, Federal Republic of Germany, 30 July–3 August 1990

  • Hirth, J.P., Lothe, J.: Theory of Dislocations, 2nd edn. Wiley, Hoboken (1982)

    MATH  Google Scholar 

  • Lauteri, G. and Luckhaus, S.: An energy estimate for dislocation configurations and the emergence of cosserat-type structures in metal plasticity. https://arxiv.org/pdf/1608.06155.pdf, Preprint (2016)

  • Lazzaroni, G., Palombaro, M., Schlömerkemper, A.: A discrete to continuum analysis of dislocations in nanowires heterostructures. Commun. Math. Sci. 13, 1105–1133 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  • Lazzaroni, G., Palombaro, M., Schlömerkemper, A.: Rigidity of three-dimensional lattices and dimension reduction in heterogeneous nanowires. Discrete Contin. Dyn. Syst. Ser. S 10(1), 119–139 (2017)

  • Leoni, G.: Lecture Notes on Epitaxy. CRM Series, Edizioni della Scuola Normale Superiore, Springer (to appear)

  • Müller, S., Palombaro, M.: Existence of minimizers for a polyconvex energy in a crystal with dislocations. Calc. Var. Partial Differ. Equ. 31(4), 473–482 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  • Müller, S., Palombaro, M.: Derivation of a rod theory for biphase materials with dislocations at the interface. Calc. Var. Partial Differ. Equ. 48(3–4), 315–335 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  • Nabarro, F.R.N.: Theory of Crystal Dislocations. Clarendon Press, Oxford (1967)

    Google Scholar 

  • Ortiz, M.: Lectures at the Vienna summer school on microstructures. Vienna, 25–29 September 2000

  • Read, W.T., Shockley, W.: Dislocation models of crystal grain boundaries. Phys. Rev. 78, 275–289 (1950)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Sussex, Pevensey 2 Building, Falmer Campus, Brighton, BN1 9QH, UK

    Silvio Fanzon & Mariapia Palombaro

  2. Dipartimento di Matematica, Sapienza Università di Roma, 00185, Rome, Italy

    Marcello Ponsiglione

Authors
  1. Silvio Fanzon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mariapia Palombaro
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marcello Ponsiglione
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcello Ponsiglione.

Additional information

Communicated by Irene Fonseca.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fanzon, S., Palombaro, M. & Ponsiglione, M. A Variational Model for Dislocations at Semi-coherent Interfaces. J Nonlinear Sci 27, 1435–1461 (2017). https://doi.org/10.1007/s00332-017-9366-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-017-9366-5

Keywords

Mathematics Subject Classification

Search

Navigation